From the cluster simulations and subsequent application of the maximum-likelihood
method (Sect. 2) the astrometric radial velocities are estimated
for the individual stars (or systems),
![]() .
Of course, the
true radial velocities
.
Of course, the
true radial velocities
![]() are also known directly from
the simulation. Thus the estimation errors
are also known directly from
the simulation. Thus the estimation errors
![]() are known. Here, index j is used to distinguish the different realisations
of the cluster model. With
are known. Here, index j is used to distinguish the different realisations
of the cluster model. With
![]() denoting an average over index k,
the following statistics are computed:
denoting an average over index k,
the following statistics are computed:
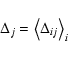 |
(4) |
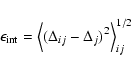 |
(5) |
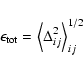 |
(6) |
The results presented below are based on solutions using the rejection limit
![]() ,
although the results for
,
although the results for
![]() are very similar.
Any conclusions from these simulations are also applicable to
the astrometric radial velocities published in Madsen et al. (2002).
are very similar.
Any conclusions from these simulations are also applicable to
the astrometric radial velocities published in Madsen et al. (2002).
In Fig. 2 (top) the internal and total standard errors of the astrometric radial velocities are shown versus the goodness-of-fit gi. The absence of any significant trend shows that gi is not a useful criterion for selecting "good" astrometric radial velocities. Even stars with gi>10 are not worse than the rest in terms of radial-velocity precision. This somewhat counter-intuitive result can be understood if the line-of-sight component of the peculiar velocities is statistically independent of the tangential component. This is obviously the case for truly random motions, but one might expect that large proper-motion errors caused by photocentric motion in binaries should be correlated with large errors in the radial component.
The bottom part of Fig. 2 shows the internal and total standard errors of the astrometric radial velocities versus the distance r from the cluster centre. In this case the standard errors clearly decrease from the centre out to 7-8 pc radius, after which they seem to increase again.
The initial decrease (for r<8 pc) is roughly in agreement with the Plummer
model in Eq. (1) for
![]() and
and
![]() pc.
pc.
In Fig. 3, the internal standard errors of the astrometric radial
velocities are plotted versus the true masses of the stars or systems (top)
and versus the absolute magnitudes (bottom). The sample is divided at 3 pc (see Sect. 3.6.2). Inside 3 pc there is a
clear difference in the velocity dispersion between the highest
masses and 1 ![]() ,
although not as much as for a full equipartition
of kinetic energy (
,
although not as much as for a full equipartition
of kinetic energy (
![]() ). The effect is much smaller outside
of 3 pc. The velocity dispersion
also seems to decline again for stars with masses less than 1
). The effect is much smaller outside
of 3 pc. The velocity dispersion
also seems to decline again for stars with masses less than 1 ![]() .
.
The effect can still be seen when the dispersion is plotted versus absolute magnitude instead of mass (Fig. 3, bottom), although the trend is less clear because of the many binary systems, for which there is no unique correspondence between system mass and total luminosity.
Together with the results of the previous section we can conclude that the
practical minimum for the internal error of the astrometric radial velocities
in the Hyades is around 0.20 km s-1, which is achieved for stars at
an intermediate distance (![]() 2-3 core radii) from the cluster centre.
At that distance there is little equipartition of kinetic energy, so it does
not matter much if more or less massive stars are selected.
2-3 core radii) from the cluster centre.
At that distance there is little equipartition of kinetic energy, so it does
not matter much if more or less massive stars are selected.
Copyright ESO 2003