It is not new to use the Hyades as a comparison with N-body simulations.
Aarseth (1977) discussed the dynamical relevance of the central
binary 80 Tau (HIP 20995) in the context of binary formation
and evolution in stellar systems as described by N-body simulations.
Oort (1979) discussed
the flattening of the Hyades parallel to the galactic plane by comparing
observations with the N-body simulations by Aarseth (1973).
Kroupa (1995c) simulated the evolution of star clusters and
found excellent agreement between the models and the Hyades luminosity
function, concluding that the initial conditions of
the cluster could to a large extent be reconstructed. An initial mass of
the Hyades protocluster of some
![]() was suggested.
Von Hippel (1998) used numerical simulations of clusters and
data on Hyades white dwarfs, among others, to conclude that the white-dwarf
mass fraction is relatively insensitive to kinematic evolution.
Portegies Zwart et al. (2001) discussed the evolution of
star clusters which were given initial conditions to represent open clusters,
including the Hyades. A good model fit to the Hyades was obtained, thus
illustrating the possibility to estimate the initial conditions
for an observed star cluster.
was suggested.
Von Hippel (1998) used numerical simulations of clusters and
data on Hyades white dwarfs, among others, to conclude that the white-dwarf
mass fraction is relatively insensitive to kinematic evolution.
Portegies Zwart et al. (2001) discussed the evolution of
star clusters which were given initial conditions to represent open clusters,
including the Hyades. A good model fit to the Hyades was obtained, thus
illustrating the possibility to estimate the initial conditions
for an observed star cluster.
What is new in the present study is that the three-dimensional kinematics of the Hyades is investigated through a direct comparison of the Hipparcos observations with a realistic N-body model, evolved till the present age of the cluster, as well as the objective to estimate the accuracy of the astrometric radial velocities from such a comparison.
Perryman et al. (1998) made a detailed study on the Hyades based on Hipparcos data and a compilation of spectroscopic radial velocities from the literature. They identified 197 probable member stars, which constitute the initial Hyades sample (Hy0) used for the present study. When comparing with the simulated cluster, only stars within 20 pc from the cluster centre are considered, due to the radial limitation in the N-body code (Sect. 3.3). Adopting the cluster centre of mass in equatorial coordinates, (+17.36,+40.87,+13.30) pc from Perryman et al. (1998), and using the kinematically improved parallaxes (Sect. 2), a subset of 178 stars (Hy0r) was found within a radius of 20 pc. The cluster has a general space velocity of (-5.90,+45.65,+5.56) km s-1 in equatorial coordinates (Madsen et al. 2002).
Perryman et al. (1998) note that a redetermination of membership with the above cited centre of mass will reduce the number of member stars outside 10 pc by 10 stars while keeping the same number of stars inside 10 pc. The true number of member stars in the Hy0r sample is then probably smaller than the 178 stars.
Hipparcos is nominally complete to
![]() for spectral
types later than G5 (or
for spectral
types later than G5 (or
![]() ). However, it is known that the actual
limit is somewhat fuzzy, due to photometric errors and other complications.
Therefore, a conservative completeness limit of
). However, it is known that the actual
limit is somewhat fuzzy, due to photometric errors and other complications.
Therefore, a conservative completeness limit of ![]() mag is assumed for
this study.
Choosing a fainter completeness limit like e.g.
mag is assumed for
this study.
Choosing a fainter completeness limit like e.g. ![]() mag will, however, not
significantly affect the outcome of the simulations as will be shown later (Table 1).
The actual number of fainter Hyades members is not known.
However, at least seven single white dwarfs have been found
(e.g. Reid 1996), and this number can also be used as a constraint
on the model.
mag will, however, not
significantly affect the outcome of the simulations as will be shown later (Table 1).
The actual number of fainter Hyades members is not known.
However, at least seven single white dwarfs have been found
(e.g. Reid 1996), and this number can also be used as a constraint
on the model.
Perryman et al. (1998) estimated the cluster age to be
![]() Myr, and this age is what is assumed in the following.
It should be mentioned that in a more recent work by Lebreton et al. (2001),
based on kinematically improved parallaxes from Dravins et al. (1997), only an upper limit of 650 Myr could be estimated due to
the lack of a clear turn-off point (cf. top diagram in Fig. 1).
In the same work they
also estimated the metallicity to
Myr, and this age is what is assumed in the following.
It should be mentioned that in a more recent work by Lebreton et al. (2001),
based on kinematically improved parallaxes from Dravins et al. (1997), only an upper limit of 650 Myr could be estimated due to
the lack of a clear turn-off point (cf. top diagram in Fig. 1).
In the same work they
also estimated the metallicity to
![]() dex.
The interstellar extinction is negligible:
Taylor (1980) found only a
very small colour excess
dex.
The interstellar extinction is negligible:
Taylor (1980) found only a
very small colour excess
![]() mag.
mag.
From various studies, a large fraction of the stars are known to be binaries.
In the compilation by Perryman et al. (1998), 75 of the 197 probable member stars were either identified as binaries in the Hipparcos
Catalogue or previously known as spectroscopic binaries (their Table 2).
Patience et al. (1998) found three new binaries from a speckle
imaging survey of Hyades members, plus one marked as binary in the Hipparcos
Input Catalogue (HIC; Turon et al. 1992), but not found by Hipparcos.
In the Tycho Double Star Catalogue (Fabricius et al. 2002), an additional
21 binaries were identified. The eclipsing binary system HIP 17962 = V471 Tau
(e.g. Werner & Rauch 1997, and references therein) must
also be included in the list of Hyades binaries.
We thus end up with 101 known binaries
in the Hy0 sample, yielding a minimum multiplicity of 0.51 companions per
primary. For the Hy0r sample (within 20 pc of the cluster centre) the minimum
multiplicity is 0.53. To include some more binary statistics, binaries with periods P < 10 days
have been taken from the compilations on the open-cluster database
WEBDA![]() .
.
The above values of the multiplicity are only lower limits to the true multiplicity, because of
the difficulty to detect binaries in some intervals of separation ![]() (or period P)
and magnitude difference
(or period P)
and magnitude difference ![]() (or mass ratio q). In restricted intervals, the
searches can however be considered complete. For instance, Hipparcos probably
detected practically all binaries with
(or mass ratio q). In restricted intervals, the
searches can however be considered complete. For instance, Hipparcos probably
detected practically all binaries with
![]() arcsec and
arcsec and
![]() ;
cf. Fig. 3.2.106 in vol. 1 of (ESA 1997), where 17 are found in Hy0r.
Patience et al. (1998) observed a high fraction
of Hyades stars that were also observed by Hipparcos. The 17 binaries
they found with
;
cf. Fig. 3.2.106 in vol. 1 of (ESA 1997), where 17 are found in Hy0r.
Patience et al. (1998) observed a high fraction
of Hyades stars that were also observed by Hipparcos. The 17 binaries
they found with
![]() arcsec and
arcsec and ![]() must therefore also
be regarded as a nearly complete sample.
must therefore also
be regarded as a nearly complete sample.
Hipparcos effectively observed for about 37 months (![]() 3 years) spread
over a period of nearly 4 years. This means that the proper
motions of binaries may be significantly affected by the orbital motion
of the photocentre, which must be taken into account when simulating the
Hyades proper motions (Sect. 3.4). In order to reduce this effect
in the observational analysis, proper motions from the Tycho-2 catalogue
(Høg et al. 2000) have also been used, where available.
In the solution for the cluster kinematics, the Tycho-2 proper motions
yield slightly, but systematically smaller radial velocities
(
3 years) spread
over a period of nearly 4 years. This means that the proper
motions of binaries may be significantly affected by the orbital motion
of the photocentre, which must be taken into account when simulating the
Hyades proper motions (Sect. 3.4). In order to reduce this effect
in the observational analysis, proper motions from the Tycho-2 catalogue
(Høg et al. 2000) have also been used, where available.
In the solution for the cluster kinematics, the Tycho-2 proper motions
yield slightly, but systematically smaller radial velocities
(
![]() HIP
HIP
![]() Tycho-2)=+0.9 km s-1) than do the Hipparcos data
for the
Tycho-2)=+0.9 km s-1) than do the Hipparcos data
for the
![]() sample (Madsen et al. 2002), which can be
explained by the mean difference of -0.4 mas yr-1 of the proper motions
in right ascension of what was considered the best sample. In declination,
the mean difference of the proper motions is 0.0 mas yr-1.
Although the expected deviations between the Hipparcos and Tycho-2 Catalogues are
generally under 0.5 mas (Urban et al. 2000), the result from
the Hyades might reflect some subtle bias in the Tycho-2 proper-motion system.
Since the Tycho-2 system of proper motions was effectively calibrated
onto the Hipparcos system, greater confidence should be put on the
solution based on the Hipparcos data.
The Tycho-2 data should therefore only be used to study the internal
velocity structure of the cluster, where a possible bias is not important.
sample (Madsen et al. 2002), which can be
explained by the mean difference of -0.4 mas yr-1 of the proper motions
in right ascension of what was considered the best sample. In declination,
the mean difference of the proper motions is 0.0 mas yr-1.
Although the expected deviations between the Hipparcos and Tycho-2 Catalogues are
generally under 0.5 mas (Urban et al. 2000), the result from
the Hyades might reflect some subtle bias in the Tycho-2 proper-motion system.
Since the Tycho-2 system of proper motions was effectively calibrated
onto the Hipparcos system, greater confidence should be put on the
solution based on the Hipparcos data.
The Tycho-2 data should therefore only be used to study the internal
velocity structure of the cluster, where a possible bias is not important.
In addition to the Hy0r sample (which thus includes all 178 probable members within a radius of 20 pc from the cluster centroid), the following samples are also discussed: Ty0r, which is the same as Hy0r but with proper motions from Tycho-2 replacing those in the Hipparcos Catalogue; Hy1r, which is the subset of 85 stars in Hy0r for which there is no known indication of multiplicity; and Ty1r, which is the same as Hy1r but with Tycho-2 proper motions.
It has been suggested that there might be systematic errors in the Hipparcos parallaxes for at least some open clusters (Pinsonneault et al. 1998). The discussion shall not be repeated here, but it should just be stated that there is a general consensus that the mean Hyades parallax is not affected by any correlation between positions and parallaxes (Narayanan & Gould 1999; van Leeuwen 2000; Lindegren et al. 2000). This problem, if it exists, has been neglected in the simulations.
The dynamical evolution of a Hyades-type open star cluster was simulated using the well-known N-body code NBODY6 (Aarseth 1999, 2000). The code incorporates algorithms to deal with stellar (including binary) encounters (Mikkola & Aarseth 1993, 1996, 1998) and stellar evolution (Hurley et al. 2000). For the present study, no modifications were made to the code. Some of the non-modelled effects are discussed in Sect. 5.
External perturbations are represented by a fixed, galactic tidal field.
The cluster is assumed to move in a circular orbit at the present distance
of the Sun from the galactic centre. The angular velocity is
![]() ,
where A=14.4 km s-1 kpc-1 and B=-12.0 km s-1 kpc-1are Oort's constants. This gives rise to tidal forces
plus a Coriolis force (cf. Chandrasekhar 1942, Ch. 5.5).
,
where A=14.4 km s-1 kpc-1 and B=-12.0 km s-1 kpc-1are Oort's constants. This gives rise to tidal forces
plus a Coriolis force (cf. Chandrasekhar 1942, Ch. 5.5).
To set up the initial cluster configuration, stars are randomly picked from
the initial mass function (IMF) described by Kroupa et al. (1993),
until the required total particle number has been reached. Binaries are included
as described below. Stars are initially deployed randomly in a Plummer potential
(Plummer 1915; Spitzer 1987) with virial radius
![]() pc. During the evolution
of the cluster, stars are kept in the simulation as long as they are within
two tidal radii (
pc. During the evolution
of the cluster, stars are kept in the simulation as long as they are within
two tidal radii (![]() 21-23 pc). The simulation is run until the cluster
reaches an age of 625 Myr.
21-23 pc). The simulation is run until the cluster
reaches an age of 625 Myr.
The reason for choosing one single age was to have a fixed parameter for comparing different model realisations. The age uncertainty is not important regarding the conclusions about the current dynamics since the cluster has been relaxed for quite a while.
Binaries are generated by randomly pairing stars picked from the IMF.
This gives an almost uniform distribution in the logarithm of the
mass ratio (![]() ), i.e. a strong preference for small q,
similar to what has been observed for G-dwarf systems (Duquennoy & Major 1991).
The semimajor axis (a) is selected from a uniform distribution in
), i.e. a strong preference for small q,
similar to what has been observed for G-dwarf systems (Duquennoy & Major 1991).
The semimajor axis (a) is selected from a uniform distribution in ![]() with an upper cut-off at 3000 AU (Quist & Lindegren 2000). The
period distribution is afterwards generated by NBODY6 based on the modelling
by Kroupa (1995a, 1995b) with minimum period 1 day, and binaries
merged if
with an upper cut-off at 3000 AU (Quist & Lindegren 2000). The
period distribution is afterwards generated by NBODY6 based on the modelling
by Kroupa (1995a, 1995b) with minimum period 1 day, and binaries
merged if
![]() .
The initial distribution of eccentricities e is assumed to be thermal,
i.e. with a probability density function 2e (Kroupa 1995b).
.
The initial distribution of eccentricities e is assumed to be thermal,
i.e. with a probability density function 2e (Kroupa 1995b).
The only free model parameters are thus the total particle number and the initial binary fraction (or multiplicity). Their determination is discussed in Sect. 3.5.
From NBODY6, the luminosity and temperature is obtained for each star.
These parameters are transformed to the observational plane
![]() using Kurucz's colour tables (e.g., Kurucz 1979;
Buser & Kurucz 1992) for
using Kurucz's colour tables (e.g., Kurucz 1979;
Buser & Kurucz 1992) for
![]() .
Johnson's V is used instead of the Hipparcos magnitude Hp, because of
the lack of adequate transformations for the latter. For binaries,
the combined colour and magnitude are calculated and plotted in order
to get results that are directly comparable with Hipparcos data.
In view of the very small interstellar reddening (Sect. 3.2),
.
Johnson's V is used instead of the Hipparcos magnitude Hp, because of
the lack of adequate transformations for the latter. For binaries,
the combined colour and magnitude are calculated and plotted in order
to get results that are directly comparable with Hipparcos data.
In view of the very small interstellar reddening (Sect. 3.2),
![]() is assumed.
is assumed.
When comparing the simulated and observed HR diagrams it should be
borne in mind that the theoretical models and colour transformations
may produce non-negligible errors. Observed discrepancies for the
Hyades amount to some 0.05 mag in ![]() or 0.3 mag in MV in the
cool end of the main sequence (Castellani et al. 2001).
No (empiric) corrections for this effect have, however, been made.
or 0.3 mag in MV in the
cool end of the main sequence (Castellani et al. 2001).
No (empiric) corrections for this effect have, however, been made.
In order to mimic the real Hyades cluster, as observed by Hipparcos, the simulated present-day cluster is "observed" from the same distance as the real Hyades and given the same centroid velocity relative the Sun. Small errors in the "observed" V magnitudes (standard deviation 0.0015 mag) are introduced, and parallaxes and proper motions, including observational errors, are generated following the same procedure as in Lindegren et al. (2000). The simulated sample includes all stars brighter than the completeness limit V=7, plus a random selection of the fainter stars matching the real sample in the number of stars per magnitude interval. It is assumed that the Hyades stars in the Hipparcos Catalogue with V > 7 mag are not subject to any selection effects, although it cannot be ruled out due to a sometimes impenetrable selection procedure of Hipparcos objects in open clusters (Mermilliod & Turon 1989).
Binaries receive different treatments depending on the magnitude
difference (![]() ), period (P), and angular separation (
), period (P), and angular separation (![]() ), in order to simulate how they were treated in the Hipparcos
data analysis (see Sect. 1.4.2 in the Hipparcos Catalogue).
Here,
), in order to simulate how they were treated in the Hipparcos
data analysis (see Sect. 1.4.2 in the Hipparcos Catalogue).
Here,
![]() ,
where subscripts "1" and "2" refer to
the primary and secondary components.
For certain combinations of these parameters, Hipparcos effectively observed
the motion of the photocentre of the system. In the remaining cases the
centre of mass were observed. The former systems include
those with
,
where subscripts "1" and "2" refer to
the primary and secondary components.
For certain combinations of these parameters, Hipparcos effectively observed
the motion of the photocentre of the system. In the remaining cases the
centre of mass were observed. The former systems include
those with
![]() to 20 years and
to 20 years and
![]() mas,
or P> 10 years and
mas,
or P> 10 years and
![]() mas; the short-period binaries
(
mas; the short-period binaries
(
![]() months), which may deviate from a single-star solution (the "stochastic"
(X) solution), although they may have been detected as binaries by Hipparcos;
and systems with Hipparcos magnitude difference
months), which may deviate from a single-star solution (the "stochastic"
(X) solution), although they may have been detected as binaries by Hipparcos;
and systems with Hipparcos magnitude difference
![]() mag.
For these systems, the component velocities
mag.
For these systems, the component velocities ![]() and
and ![]() are combined into a single velocity of
the photocentre,
are combined into a single velocity of
the photocentre,
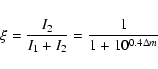 |
(3) |
The resulting simulated astrometric data are subject to exactly the same maximum-likelihood estimation procedure as was used for the real cluster (Lindegren et al. 2000). In particular, astrometric radial velocities and kinematically improved parallaxes are derived for the individual stars or binaries. The error in the estimated parallaxes is in the range 0.2-1.0 mas (an error of 0.5 mas corresponds to approximately 1 pc in the cluster centre). The improved parallaxes are used to compute distances from the cluster centre, which allow to count the number of stars within a certain radius. Furthermore, for any subsample of the stars, the velocity dispersion can be estimated from the proper-motion residuals (Sect. 2).
In order to tune the model parameters, it is necessary to make several
simulations for the same parameter values but using different
initialisations of the random number generator. The average of the
different random realisations is then compared with the observational
data, and the input parameters adjusted accordingly.
The quantities to be compared are the radial distribution of the stars,
their total number above a given magnitude limit, and binary statistics.
Also the number of giants (defined as MV<1 and
![]() )
and
the number of single white dwarfs are used to constrain the model.
)
and
the number of single white dwarfs are used to constrain the model.
| observed parallaxes: | estimated parallaxes: | true parallaxes: | |||
| constraint |
|
|
|
|
|
|
|
173 |
|
178 | 166.7 |
167.6 |
| 134 |
|
143 | 149.5 |
153.1 |
|
| 83 |
|
88 | 81.3 |
82.4 |
|
| 57 |
|
58 | 61.8 |
62.7 |
|
| 30 |
|
38 | 37.0 |
47.8 |
|
| 24 |
|
29 | 30.2 |
39.0 |
|
| Giants ( |
5 |
|
5 | 5.1 |
5.1 |
| single white dwarfs | 8.5 |
||||
The finally adopted (protocluster) model comprises 200 single stars and 1200 binaries, i.e. an initial multiplicity of 0.86 companions per primary.
The total initial mass is 1100-
![]() .
This is slightly less
than previous estimates of 1200-
.
This is slightly less
than previous estimates of 1200-
![]() (Reid 1993)
or
(Reid 1993)
or
![]() (Kroupa 1995c). This smaller initial mass
was found necessary in order to correctly reproduce the number of
observed stars with the given IMF. The true initial mass of the Hyades is
probably higher due to non-modelled mass loss (Sect. 5).
According to the simulations, the total current mass of the Hyades stars is
(Kroupa 1995c). This smaller initial mass
was found necessary in order to correctly reproduce the number of
observed stars with the given IMF. The true initial mass of the Hyades is
probably higher due to non-modelled mass loss (Sect. 5).
According to the simulations, the total current mass of the Hyades stars is
![]() 460
460 ![]() with a tidal radius of
with a tidal radius of ![]() 11 pc.
Observationally, Reid (1992) made the estimation 410-480
11 pc.
Observationally, Reid (1992) made the estimation 410-480
![]() while Perryman et al. (1998) estimated
while Perryman et al. (1998) estimated
![]() in their Hipparcos study of the cluster.
in their Hipparcos study of the cluster.
An example of the observational HR diagram for one of the model realisations is shown in Fig. 1, together with the corresponding observed diagram for the Hyades cluster. In addition to the standard deviation introduced in V, a standard deviation of 0.01 in B-V is also introduced in the model HR diagram to make the colour distribution appear more realistic. This standard deviation includes both observational errors and the effects of peculiar stars, stellar rotation, etc. Apart from the previously mentioned possible discrepancy in the cool end of the main sequence, and the fact that the giant stars are too red in the simulations, the general agreement is reasonable. The precise colours of the giants are, however, irrelevant in the context of this study.
Table 1 shows some statistics computed from this model, after
evolution to an age of 625 Myr and transformation to the observables, together
with the corresponding observed numbers.
From Table 1 it appears that the distribution of stars with radial distance
and apparent magnitude in the Hyades is well reproduced by the model cluster.
The number of stars decreases when we go from the constraints based on
the true parallaxes to the constraints based on the estimated parallaxes,
and the number decreases even further when we use the observed parallaxes.
This is a result of observational errors affecting the parallaxes, and
mostly for the smallest sphere ![]() .
In fact, the resemblence in the three columns is so good that it shows the modelling
of the errors are in accordance with reality.
The underabundance of stars in the models relative to the observations
in the range
10 < r < 20 pc can be explained by an overestimation
of stars outside 10 pc by Perryman et al. (1998). They
argued that using another centre of mass in the Hyades would lead
to fewer stars in the halo (Sect. 3.2).
.
In fact, the resemblence in the three columns is so good that it shows the modelling
of the errors are in accordance with reality.
The underabundance of stars in the models relative to the observations
in the range
10 < r < 20 pc can be explained by an overestimation
of stars outside 10 pc by Perryman et al. (1998). They
argued that using another centre of mass in the Hyades would lead
to fewer stars in the halo (Sect. 3.2).
It has been much more difficult to reproduce the observed binary statistics (Table 2). Bright binaries with high mass ratio or small magnitude difference are underproduced. Even if every star in the protocluster were assumed to be a binary (multiplicity 1.0), the model would still predict too few binaries of these characteristics. The observed sample also has significantly more known short-period binaries (P<10 days) than obtained in the simulations. These discrepancies indicate that the model distributions in mass ratio and/or semi-major axis would need some adjustment. Alternatively, a higher initial mass leading to more binaries with the required properties could be an explanation assuming non-modelled mass loss of preferentially low mass stars. However, the discrepancies are not dramatic and for the present study it was preferred not to change the relevant code in NBODY6.
| Constraint |
|
|
|
|
||
| binaries, all |
|
|
| binaries,
|
17 |
|
| binaries,
|
17 |
|
| binaries, P<10 days |
|
|
Since the initial multiplicity must be very high to fit the observed binary statistics without being in contradiction with the observed number of Hyades member stars, the degree of degeneracy between the two free input parameters (initial particle number and initial multiplicity) is small.
|
The simulations could in principle be "inverted" to derive an age, by for instance stopping the modelling when the realisations appear similar to observed structural or dynamical features in the Hyades. But the non-modelled effects leading to mass loss during the dynamical evolution will be a major uncertainty (Sect. 5).
In a Plummer potential, the velocity dispersion decreases with cluster radius according to Eq. (1). At some radius, however, the relation is expected to break down when the stars have left the cluster potential and become subject to the Galactic field. In the following this possible structure is investigated.
The various observed samples (Hy0r, Hy1r, Ty0r, Ty1r), as well as the different
realisations of the adopted cluster model, are analysed by means of the
maximum-likelihood method mentioned in Sect. 2. The samples
are divided according to distance (r) from the cluster centroid in order
to determine if there is a radial variation of the kinematics. The ranges in r have not been chosen at random: 3 pc is approximately the core radius
while 10 pc is approximately the tidal radius.
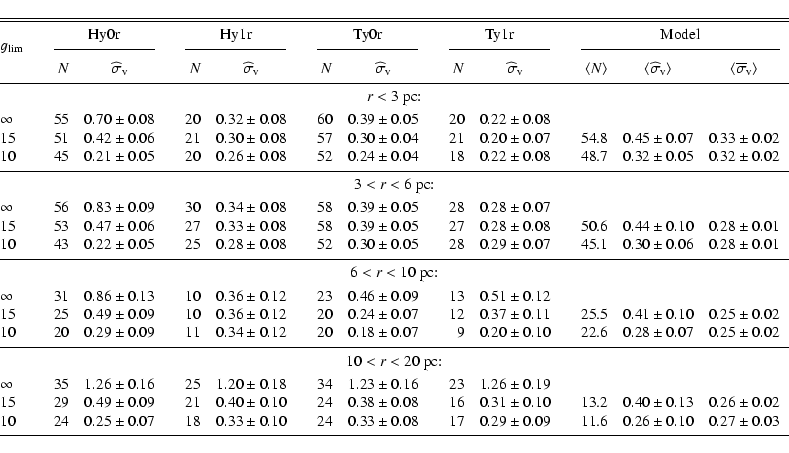
Table 3 summarises the results for the number N of stars
(or systems) and the estimated velocity dispersion
![]() .
.
The analysis method includes the rejection procedure designed to "clean" the
cluster membership described in Sect. 2 with the
goodness-of-fit statistic gi calculated for each star.
For the model simulations, no results
are given for
![]() because of their sensitivity to run-away
stars. In the observed sample such cases were already removed by Perryman
et al. (1998).
It should be noted that the cleaning process successively reduces the
estimated internal velocity dispersion, because the latter is based on the
proper-motion residuals, which are also reflected in gi. This is most
clearly seen for the Hy0r sample at all radii, and for the other samples
at r>10 pc.
The reason that there seems to be more stars for e.g. Ty1r at
because of their sensitivity to run-away
stars. In the observed sample such cases were already removed by Perryman
et al. (1998).
It should be noted that the cleaning process successively reduces the
estimated internal velocity dispersion, because the latter is based on the
proper-motion residuals, which are also reflected in gi. This is most
clearly seen for the Hy0r sample at all radii, and for the other samples
at r>10 pc.
The reason that there seems to be more stars for e.g. Ty1r at
![]() than
than
![]() for certain ranges in r is that kinematically
improved parallaxes have been used to calculate the distance from cluster centre.
Since it is a different solution for each
for certain ranges in r is that kinematically
improved parallaxes have been used to calculate the distance from cluster centre.
Since it is a different solution for each
![]() ,
the kinematically
improved parallaxes may change slightly.
,
the kinematically
improved parallaxes may change slightly.
Kinematically, one cannot in general distinguish between actual non-member
stars and member stars with a deviating space motion. The most probable
reason for a member star not to follow the common space motion of the
cluster is that it is a binary in a non-modelled orbit.
As explained in Sect. 3.2, this effect should be greater for the
samples based on the Hipparcos proper motions than when using the Tycho-2
data. Comparing the results for Hy0r and Ty0r as function of
![]() suggests that binaries are the main cause for deviating proper motions
out to
suggests that binaries are the main cause for deviating proper motions
out to
![]() pc, while for the greater radii they are partly caused
by actual non-members.
pc, while for the greater radii they are partly caused
by actual non-members.
The last two columns in Table 3 show the estimated and
true dispersions from 20 realisations of the model. It appears that
![]() yields a correct estimation of the dispersion,
while
yields a correct estimation of the dispersion,
while
![]() leads to an over-estimation of
leads to an over-estimation of
![]() .
Using
.
Using
![]() ,
the cluster as a whole (inside 20 pc)
yields a dispersion of
,
the cluster as a whole (inside 20 pc)
yields a dispersion of
![]() km s-1, with no clear
dependence on r. The model cluster yields a slightly larger value
(0.30 km s-1) and shows a 20% decrease from the centre outwards.
It should be noted that two of the 20 models yield estimated values
as small as the observations (
km s-1, with no clear
dependence on r. The model cluster yields a slightly larger value
(0.30 km s-1) and shows a 20% decrease from the centre outwards.
It should be noted that two of the 20 models yield estimated values
as small as the observations (![]() 0.23 km s-1). The dispersions
0.23 km s-1). The dispersions
![]() characterise the stars in the simulated Hyades
sample, and not the total number of stars in the cluster. Due to the
limiting magnitude, stars with masses less than 0.5-0.6
characterise the stars in the simulated Hyades
sample, and not the total number of stars in the cluster. Due to the
limiting magnitude, stars with masses less than 0.5-0.6 ![]() do not contribute to the velocity dispersions in the table, just
as with the observations.
do not contribute to the velocity dispersions in the table, just
as with the observations.
Madsen et al. (2001) found some rather large radial variations of the velocity dispersion in the Hyades, but could not conclude whether the structure was real or not. From the present simulations it is concluded that the observed structure is probably spurious: similar variations (of either sign) can be seen in some of the model realisations, although they are absent in the average of the realisations.
Hitherto in studies of open clusters, only in the Pleiades has an indication of
a relationship between r and (the tangential component of)
![]() been found (van Leeuwen 1983).
In the globular cluster M 15, however, a velocity dispersion decreasing
from the centre out to 7 arcmin and then increasing was found by
Drukier et al. (1998). They interpreted it as an indication of
heating of the outer part of the cluster by the galactic tidal field. But how the
minimum at 7 arcmin was related to the tidal radius or other quantities remained unclear.
Heggie (2001) argued that heating might be an incorrect interpretation since the
effect can also be seen in N-body simulations of star clusters moving under
influence of a steady tidal field (cf. Giersz & Heggie 1997).
In the models here, the same trend is seen, with a minimum in the
been found (van Leeuwen 1983).
In the globular cluster M 15, however, a velocity dispersion decreasing
from the centre out to 7 arcmin and then increasing was found by
Drukier et al. (1998). They interpreted it as an indication of
heating of the outer part of the cluster by the galactic tidal field. But how the
minimum at 7 arcmin was related to the tidal radius or other quantities remained unclear.
Heggie (2001) argued that heating might be an incorrect interpretation since the
effect can also be seen in N-body simulations of star clusters moving under
influence of a steady tidal field (cf. Giersz & Heggie 1997).
In the models here, the same trend is seen, with a minimum in the
![]() relation just inside 10 pc (the mean tidal radius of the models
is between 10 and 11 pc).
relation just inside 10 pc (the mean tidal radius of the models
is between 10 and 11 pc).
Theoretically we should also expect a decreasing velocity dispersion with higher mass, or correspondingly lower absolute magnitude, due to equipartition of kinetic energy. This should in turn lead to dynamical mass segregation, with the massive stars more concentrated to the centre of the cluster. This effect may have been seen in IC 2391 (Sagar & Bhatt 1989) and Praesepe (Holland et al. 2000). Perryman et al. (1998) found a clear mass segregation in the Hyades from the number density of stars in various mass groups as a function of distance from the centre. Direct searches by Lindegren et al. (2000) and Madsen et al. (2001) for a relation between the observed velocity dispersion and mass (or absolute magnitude), did however prove inconclusive. Evidence of any equipartition of kinetic energy is best sought among the stars in the core of the cluster (Inagaki & Saslaw 1985). For the present study, a limiting radius of 3 pc is therefore used. This is approximately the core radius of the Hyades.
In the Hipparcos Catalogue, often only the common absolute magnitude for a binary is available, and not the absolute magnitudes for both components. Since it is the mass that is interesting, only the samples without known binaries should be used, to ensure a reasonably unique correspondence between absolute magnitude and mass. In the simulated samples, binaries with a difference in absolute magnitude between the combined absolute magnitude of the two components in the binary and the primary component of more than 0.1 mag have been removed. This is the simplest way to simulate the hy1r sample.
The remaining stars with r<3 pc in the hy1r sample are separated in four intervals
of absolute magnitude, with divisions at MV=2.1, 3.4, and 5.4 mag,
approximately corresponding to the masses 1.8, 1.4, and
![]() .
The estimated dispersions in these intervals are
.
The estimated dispersions in these intervals are
![]() ,
,
![]() ,
,
![]() km s-1, and no solution for the
last interval. The uncertainties are too large to allow any firm conclusion,
although the expected trend is there. For comparison, the simulations gave
an average dispersion going from 0.28 to 0.36 km s-1 in the same
intervals.
km s-1, and no solution for the
last interval. The uncertainties are too large to allow any firm conclusion,
although the expected trend is there. For comparison, the simulations gave
an average dispersion going from 0.28 to 0.36 km s-1 in the same
intervals.
Several studies of the velocity dispersion of the Hyades have been performed during the years.
In a detailed discussion by Gunn et al. (1988), who performed a spectroscopic
investigation of the cluster, a mean dispersion of 0.23 km s-1 was derived from a Plummer
model. Their result agreed with the velocity dispersion obtained from
the most precise spectroscopic radial velocities
in their Hyades sample. However, it is important to note that the result of 0.23 km s-1 is
dependent on the estimated M and ![]() ,
where the mass is the major uncertainty.
Perryman et al. (1998) also used a Plummer model and got 0.21 km s-1 for the
central velocity dispersion. Again this value was derived by estimating the mass
and the core radius.
Compared to this work the values are 50% lower, but can be explained by
the uncertainty in the estimation of the masses.
Makarov et al. (2000) used Tycho-2 proper motions to discuss the
velocity dispersion of the Hyades, and found the velocity dispersion to
be 0.32 km s-1 for the stars with the most precise proper motions.
If known spectroscopic binaries were removed, the velocity dispersion decreased
to 0.22 km s-1. The last value agrees well with the value obtained
with Tycho-2 proper motions in Table 3.
,
where the mass is the major uncertainty.
Perryman et al. (1998) also used a Plummer model and got 0.21 km s-1 for the
central velocity dispersion. Again this value was derived by estimating the mass
and the core radius.
Compared to this work the values are 50% lower, but can be explained by
the uncertainty in the estimation of the masses.
Makarov et al. (2000) used Tycho-2 proper motions to discuss the
velocity dispersion of the Hyades, and found the velocity dispersion to
be 0.32 km s-1 for the stars with the most precise proper motions.
If known spectroscopic binaries were removed, the velocity dispersion decreased
to 0.22 km s-1. The last value agrees well with the value obtained
with Tycho-2 proper motions in Table 3.
Copyright ESO 2003