A&A 401, 243-263 (2003)
DOI: 10.1051/0004-6361:20021865

On the radio afterglow of gamma ray bursts

S. Dado¹ - A. Dar ¹ - A. De Rújula²

1 - Physics Department and Space Research Institute, Technion Haifa 32000, Israel
2 - Theory Division, CERN, 1211 Geneva 23, Switzerland

Received 2 May 2002 / Accepted 21 November 2002

Abstract
We use the cannonball (CB) model of gamma ray bursts (GRBs) to predict the spectral and temporal behaviour of their radio afterglows (AGs). A single simple expression describes the AGs at all times and frequencies; its high-frequency limit reproduces the successful CB model predictions for optical and X-ray AGs. We analyze all of the observed radio AGs of GRBs with known redshifts, including those of the exceptionally close-by GRB 980425. We also study in detail the time-evolution of the AGs' spectral index. The agreement between theory and observations is excellent, even though the CB model is extremely frugal in the number of parameters required to explain the radio observations. We propose to use the scintillations in the radio AGs of GRBs to verify and measure the hyperluminal speed of their jetted CBs, whose apparent angular velocity is of the same order of magnitude as that of galactic pulsars, consistently measured directly, or via scintillations.

Key words: gamma-rays: bursts

1 Introduction

The Cannonball Model is based on the hypothesis that GRBs and their afterglows are made in supernova explosions by the jetted ejection of relativistic plasmoids: ``cannonballs'' made of ordinary baryonic matter (Dar & De Rújula 2000a), similar to the ones observed in quasars and microquasars (e.g., Mirabel & Rodriguez 1994, 1999 and references therein). The name cannonball (CB) originates in the contention that - due to a mechanism that we have explicitly discussed in Dado et al. (2001) - the ejected plasmoids stop expanding very early in the afterglow (AG) phase.

The CB paradigm gives a good description of the properties of the $\gamma$-rays in a GRB, that we modelled in simple approximations in Dar & De Rújula (2000b). It suggests an alternative (Dar & De Rújula 2001a), which is rather promising (Dado et al. 2002), to the ``Fe-line'' interpretation of the spectral lines observed in some X-ray afterglows (GRB 970508: Piro et al. 1998; GRB 970828: Yoshida et al. 1999, 2001; GRB 991216: Piro et al. 2000; GRB 000214: Antonelli et al. 2000). The model also provides an extremely simple and successful description of the spectrum, and of the shape and absolute magnitude of the light curves of the optical and X-ray afterglows of all GRBs of known redshift, at all observed times (Dado et al. 2001, hereafter called DDD 2001). This description is universal, it encompasses the early optical flash of GRB 990123, the very peculiar optical and X-ray AG of GRB 970508, and all of the properties of GRB 980425, associated with SN1998bw.

In this paper we derive the CB model's predictions for radio afterglows, and compare them to all radio observations in GRBs of known redshift. We also study the evolution of the spectral index of AGs as a function of time. The CB model - in parameter-thrifty and very simple terms - passes these tests with flying colours.

2 Summary

In the CB model a GRB jet consists of $n_{_{\rm CB}}$ cannonballs, typically a few, each of them generating a prominent pulse in the $\gamma$-ray signal, as they reach the transparent outskirts of the shell and/or prior ``wind" of their associated supernova (SN). We assume CBs to be made of ordinary matter, mainly hydrogen, and to enclose a magnetic field maze, as is the case for the observed ejections from quasars and microquasars. The interstellar medium (ISM) the CBs traverse in the AG phase has been previously partially ionized by the GRB radiation and is fully ionized by Coulomb interactions as it enters the CB. In analogy to processes occurring in quasar and microquasar ejections, the ionized ISM particles are multiple scattered, in a ``collisionless'' way, by the CBs' turbulent magnetic fields. In the rest system of the CB the ISM swept-up nuclei are isotropically re-emitted, exerting an inwards force on the CB's surface. This allows one to compute explicitly the CB's radius as a function of time (DDD 2001). The radius, for typical parameters, and in minutes of observer's time, reaches a constant $R_{\rm max}$ of a few times 10¹⁴ cm.

The ISM nuclei (mainly protons) that a CB scatters also decelerate its flight: its Lorentz factor, $\gamma(t)$, is calculable. Travelling at a large $\gamma$ and viewed at a small angle $\theta$, the CB's emissions are strongly relativistically aberrant: in minutes of observer's time, the CBs are parsecs away from their source. For a constant CB radius and an approximately constant ISM density, $\gamma(t)$ has an explicit analytical expression, as discussed in Appendix A. Typically $\rm\gamma=\gamma(0)/2$ at a distance of order 1 kpc from the source, and $\gamma(0)\sim 10^3$. Due to a limited observational sensitivity, GRBs have been detected only up to angles $\theta$ of a few times $1/\gamma(0)$.

The ISM electrons entering a CB are caught up and bounce off its enclosed magnetic domains acquiring a predictable power-law energy spectrum, as we argue in Sect. 3. In the CB's rest system ${\rm d}n_{e}/{\rm d}E\propto E^{-2}$ below an energy $E_{\rm b}(t)\simeq \gamma(t)\, m_{e}\, c^2$, steepening to ${\rm d}n_{e}/{\rm d}E\propto E^{-(p+1)}$, with $p\simeq 2.2$, above this energy. The energy $E_{\rm b}$ does not correspond to the conventional synchrotron ``cooling break'' but to the injection bend at the energy at which electrons enter the CB with a Lorentz factor $\gamma(t)$. In Sect. 4 we discuss the observational support of the existence of the injection bend, which is strong. Given the very large magnetic and radiation energy densities in the CB, the usual cooling break (at the energy at which the energy-loss rate due to synchrotron emission and inverse Compton scattering equals that due to bremsstrahlung, adiabatic losses and escape) happens only at subrelativistic energies, as discussed in Appendix B. The magnetic energy-density in a CB (DDD 2001) is:

$$U_B= {B^2\over8\, \pi}\sim {1\over 4}\,\gamma^2\,n_p\, m_p\, c^2,$$ (1)

with n_p the ISM baryon density (seen as $\gamma\, n_p$ by the CB in its rest system). Thus, the magnetic field is:

$$B(t)\sim 3 \;\left[{n_p\over 10^{-3}\,{\rm cm}^3}\right]^{1/2} \left[{\gamma(t)\over 10^3}\right]\; {\rm Gauss}.$$ (2)

The pitch-angle averaged characteristic synchrotron-radiation frequency of electrons of energy $E=E_{\rm b}$ is (Rybicki & Lightman 1979):

$$\nu_{\rm b}(t)\sim 0.29\,{3\over 4}\; \gamma(t)^2\,\nu_{\rm L}$$ (3)

where $\nu_{\rm L}=e\,B/(2\,\pi\,m_{e}\,c)$ is the Larmor frequency in the CB enclosed magnetic field B. To a good approximation, in the CB rest system and prior to cumulation, absorption and limb-darkening corrections, the synchrotron radiation has a spectral shape:

$$\nu\,{{\rm d}n_\gamma\over {\rm d}\,\nu} \propto f_{\rm sync... ...{\rm b}(t)]^{-1/2}\over \sqrt{1+[\nu/\nu_{\rm b}(t)]^{(p-1)}}}$$

$$K(p) \equiv {\sqrt{\pi}\over \Gamma\left[{2\, p-1\over 2(p-1... ...ft[{2\, p-3\over 2(p-1)}\right]} \simeq{p-2\over 2\,(p-1)}\; ,$$ (4)

where we have normalized $f_{\rm sync}(\nu)$ to a unit integral over all frequencies and the approximation is good to better than 8% precision in the range $2<p\leq 2.6$. Note that, for $\nu\gg\nu_{\rm b}$, $f_{\rm syn}\propto \nu_{\rm b}^{(p-2)/2}$ i.e., it is independent of $\nu_{\rm b}$ for p=2. For $p\sim 2.2,$ the extremely weak dependence of $f_{\rm syn}$ on $\rm\nu_b$ in the optical and X-ray bands was neglected in DDD 2001.

For the first $\sim$10³ s of observer's time, a CB is still cooling fast and emitting via thermal bremsstrahlung (DDD 2001), but after that the CB emissivity integrated over frequency is equal to the energy deposition rate of the ISM electrons in the CB:

$${{\rm d}E\over {\rm d}t} \simeq \eta\, \pi\, R_{\rm max}^2\, n_{e}\, m_{e}\, c^3\, \gamma(t)^2,$$ (5)

where $n_{e}\gamma$ is the ISM electron density in the CB rest system and $\eta$ is the fraction of ISM electrons that enter the CB and radiate there the bulk of their incident energy. In the early afterglow Eq. (5) must be modified to account for the fact that the bulk of the radio emission by the incoming ISM electrons is delayed by the time it takes them to cool down to energies much lower than their initial one. This implies that Eq. (5) must be modified by a multiplicative ``cumulation factor'' ${\rm C}(\nu,t)$, which is $\approx$1 at optical and X-ray wavelengths, as discussed in detail in Sect. 5. Two other factors, discussed in Sects. 6 and 7, distinguish radio waves from higher-frequency emissions: attenuation by self-absorption and limb darkening; they introduce two extra factors $A_{_{\rm CB}}[\nu]$and $L_{_{\rm CB}}(\nu,\theta_{_{\rm CB}})$, with $\theta_{_{\rm CB}}$ a direction of emission relative to the CB's velocity vector. Normalized as in Eq. (5) and corrected by all these factors, the afterglow energy flux density of a CB, in its rest system, is:

 

$$F_{_{\rm CB}}[\nu,t,\theta_{_{\rm CB}}] \simeq \eta\, \pi\,R_{\rm... ...nu,t) C(\nu,t)\, A_{_{\rm CB}}[\nu]\, L_{_{\rm CB}}(\nu,\theta_{_{\rm CB}})\, ,$$ (6)

to be summed over $n_{_{\rm CB}}$ for a jet with that number of cannonballs. This expression, for $\rm\nu \gg \nu _b$ and the second row set to unity, reproduces the optical and X-ray AG result discussed in DDD 2001.

An observer in the GRB progenitor's rest system, viewing a CB at an angle $\theta$ (corresponding to $\rm\theta_{_{CB}}$ in the CB's proper frame), sees its radiation Doppler-boosted by a factor $\delta$:

$$\delta(t)\equiv {1\over\gamma(t)\,(1-\beta(t)\cos\theta)} \simeq {2\,\gamma(t)\over 1+\theta^2\gamma(t)^2},$$

 

$$\cos\theta_{_{\rm CB}}= {\cos\theta-\beta(t)\over 1-\beta(t)\,\cos\theta} \simeq{1-\theta^2\gamma(t)^2\over1+\theta^2\gamma(t)^2}$$ (7)

where the approximations are valid in the domain of interest for GRBs: large $\gamma$ and small $\theta$. Since the CB is catching-up with the radiation it emits, $\delta$ is also the relative time aberration: ${\rm d}t_{\rm obs}={\rm d}t_{_{\rm CB}}/\delta$. The observed spectral energy density is modulated by a factor $\delta^3$, two powers of $\delta$ reflecting the relativistic forward collimation of the radiation emitted in the CB's rest system. The AG spectral energy density $F_{\rm obs}$seen by a cosmological observer at a redshift z (Dar & De Rújula 2000a), is:

$$F_{\rm obs}[\nu,t]\simeq {A_{\rm Gals}\, (1+z)\,\delta^3 ... ...[{(1+z)\,\nu\over\delta(t)},{\delta(t)\,t\over 1+z} \right] ,$$ (8)

where $A_{\rm Gals}$ represents the absorption in the host galaxy and the Milky Way, $F_{_{\rm CB}}$is as in Eq. (6), and $D_{\rm L}$ is the luminosity distance (we use throughout a cosmology with $\Omega=1$ and $\Omega_\Lambda=0.7$). In the CB model, the extinction in the host galaxy may be time dependent: in a day or so, CBs typically move to kiloparsec distances from their birthplace, where the extinction should have drastically diminished.

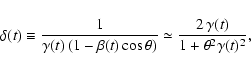
In DDD 2001 we fit, in the CB model, the R-band AG light curves of GRBs. The fit involves five parameters per GRB: the overall normalization; $\theta$: the viewing angle; $\gamma_0$: the t=0 value of the Lorentz factor; $x_\infty$: the ``deceleration'' parameter of the CBs in the ISM; and the spectral index p. The value of p, obtained from the temporal shape of the afterglow, is in every case very close to the expectation p=2.2, and - within the often large uncertainties induced by absorption - with the observed spectra from optical frequencies to X-rays (DDD 2001).

In this paper we complete our previous work by making broad-band fits to the data at all available radio and optical frequencies. In so doing, we need to introduce just one new ``radio'' parameter: an ``absorption frequency'' $\rm\nu_a$, corresponding to unit CB opacity at a reference frequency. We set p=2.2 so that the extension to a broad-band analysis does not involve an increase in the total number of parameters. We have to refer very often to the values of the parameters that our previous experience with the CB model made us choose as reference values. For convenience, these are listed in Table 1.

 

Table 1: Reference parameters^a.

The predictions of the CB model, for typical parameters, are summarized in Fig. 1. The energy density spectra at radio to optical frequencies are shown, at various times after the GRB, in the upper panel. The spectral slopes before and soon after the peak frequency are $\rm 3/2$ and -(p-1)/2, as indicated. The spectra peak at a frequency at which self-attenuation in the CBs results in an opacity of $\cal {O}$(1). At frequencies well above the frequency $\rm\nu_b$ characterizing the injection bend, the spectrum steepens to a slope -p/2. In the figure's lower panel we show light curves at various radio frequencies. At large times and for $\rm\nu \gg \nu _b$ - which is the case at all frequencies in the example of Fig. 1, whose parameters are close to those of GRB 000301c - they tend to $t^{-2\,(p+1)/3}$, this behaviour being reached at earlier times, the higher the frequency. For $\rm\nu\ll \nu_b$, the corresponding limiting behaviour is $\approx$t^-4/3, observable at low frequencies in the cases of GRBs 991216, 991208 and 000418. All of the above predictions are robust: they do not depend on the detailed form of the attenuation, cumulation and limb-darkening factors. The early rise of the light curves does depend on such details, on which we shall have to invest a disproportionate effort in Sects. 5 to 7.

Figure 1: Typical predictions for the CB model's radio afterglow. Upper panel: spectra at different times, from 1 to 300 days. The peak frequencies correspond to CB self-opacities of $\cal {O}$(1). The black dots are the location of the synchrotron frequency corresponding to the injection bend. Lower panel: Light curves at different radio frequencies, from 350 to 1.43 GHz. The asymptotic curve is $t^{-2\,(p+1)/3}$(for $\rm\nu \gg \nu _b$, as is the case at all frequencies shown in this figure).

Open with DEXTER

The CB model provides an excellent description of the data, as discussed in Sects. 4, 8 and 9. In the case of GRB 980425, for which the optical AG is dominated by SN1998bw, we used the parameters that fit its X-ray afterglow (DDD 2001) and the GRB's fluence (Dar & De Rújula 2000a) to argue that they are not exceptional. The CB-model's description of the radio data for this GRB/SN pair is excellent: there is nothing peculiar about this GRB, nor about its associated supernova, as we discuss in detail in Sect. 9, along with the question of the angular separation in the sky of the SN and the associated CBs, which may have been, or may still be, observable.

The apparent sky velocities of cosmological CBs are extremely superluminal and their angular velocities happen to be of the same order of magnitude as those of galactic pulsars. This implies that CB velocities can possibly be extracted from their observed radio scintillations, as discussed in Sect. 12.

3 The electron spectrum

3.1 Numerical simulations

The acceleration of charged particles by a moving CB is not substantially different from some of the cases already studied in the literature, the acceleration of cosmic rays and electrons having attracted an enormous amount of attention since Fermi's first analysis in 1949 (for an excellent introduction, see Longair 1994). The most efficient and thus promising mechanism is the ``first-order'' acceleration of particles by fast-moving shocks, extensively studied analytically and numerically since the pioneering works of Axford et al. (1977), Krymsky (1977), Bell (1978) and Blandford & Ostriker (1978). The analysis closest to the case at hand is that of Ballard & Heavens (1992), who studied acceleration by relativistic shocks, with the charged particles deflected by highly disordered magnetic fields, rather than, as it is generally assumed, by small irregularities in an otherwise uniform field. The ``relativistic'' and ``chaotic'' inputs are what make this work particularly relevant to the case of particle acceleration by and within CBs.

Ballard and Heavens study numerically, for various values of a moving discontinuity's Lorentz factor ranging up to $\rm\gamma_s=5$, the result of its collision with an isotropic ensemble of particles with $\rm\gamma_p=100$. They find that, for $\rm\gamma_s=5$, the resulting particle energy distribution has a break (in this reference system) at $\rm\gamma\sim 10\, \gamma_p$, at which point it steepens. The particles below the break have a dominantly very forward motion: they are the ones which have been upscattered just once. Given this hint, it is easy to reproduce the numerical results in an analytic approximation. In the shock's rest system, the energy of the particles that have been scattered only once is equal to their incoming energy: the break in the spectrum seen in the simulations is a kinematical break occurring roughly at the injection energy. ``Observed'' in the system in which the shock is travelling at $\rm\gamma_s=5$, this injection bend is very reminiscent of the familiar synchrotron-cooling ``break'', but it has little to do with it; indeed, in the simulations of Ballard & Heavens (1992) cooling was entirely neglected.

3.2 A simple analysis

Consider the CB in its rest system and temporarily postpone the discussion of cooling. The ISM electrons impinge on the CB in a fixed direction with a Lorentz factor equal to that of the CB in the GRB progenitor's rest system, $\gamma_{\rm e}=\gamma(t)$. The electrons not having ``bounced back'' off the CB's strong magnetic field, or having done it only once, retain the incoming energy, $E_{\rm b}(t)=\gamma(t)\,m_{e}\, c^2$, so that their energy distribution is: ${\rm d}n_{e}/{\rm d}E\propto \delta[E-E_{\rm b}(t)]$. A very robust (i.e. detail independent) feature of the studies of acceleration by relativistic shocks is that the particles having bounced more than once acquire a spectrum ${\rm d}n_{e}/{\rm d}E\propto E^{-p}$, with p=2 in analytical approximations and $p\sim 2.2$in numerical simulations. A few bounces are sufficient to attain such a spectrum. The CB is a system of finite transverse dimensions and the magnetic field contrast between its interior and its exterior is very large. Thus, we do not expect the same electron to bounce many times off the CB, as the latter catches up with it. The acceleration should occur mainly within the CB as charged particles bounce off its chaotically moving magnetic domains, and it should be very fast and efficient, since the injection is highly relativistic and there is no distinction between ``first and second order Fermi'' processes. The overall ``source'' spectrum of relativistic electrons is:

 

$${{\rm d}n_e^{\rm s}\over {\rm d}{E}}\sim A_1(t)\,E_{\rm b}(t)\,\d... ... A_2(t)\,\Theta[E-E_{\rm b}(t)] \left[{E\over E_{\rm b}(t)}\right]^{-p}\!\!\! ,$$ (9)

with A₁ and A₂ of comparable magnitude and a time dependence which is that of the rate, $\eta\,\pi\,R_{\rm max}^2\,c\,n_{e}\,\gamma(t)$, at which electrons enter the CB.

3.3 The spectrum of cooled electrons

The electron energy loss by synchrotron radiation is:

$$-{{\rm d}E\over {\rm d}t}= A_{\rm S}\,\beta^2\,E^2 ,$$

$$A_{\rm S} \equiv {B^2\over 6\,\pi}\,{\sigma_{\rm T}\,c\over (m_{e}\,c^2)^2}\, ,$$ (10)

with $\beta\approx 1$ for the relativistic energies of interest and $\sigma_{\rm T}=0.665$ barn the Thomson cross-section. Let the rate at which fresh electrons are supplied by the ISM be called R. The electron source distribution of Eq. (9) ``ages'' by cooling so that:

$${\partial\over\partial t}\left[{{\rm d}n_{e}\over {\rm d}E}\r... ...{\rm d}E}\right]+ R\,{{\rm d}n_{e}^{\rm s}\over {\rm d}E}\cdot$$ (11)

At times longer than the synchrotron cooling time, the electron distribution tends to a time-independent ${{\rm d}n_{e}/ {\rm d}E}$, obtained by equating to zero the l.h.s. of Eq. (11) and integrating it with the source function of Eq. (9):

 

$${{\rm d}n_{e}\over {\rm d}E}\sim A_1(t)\,\Theta[E_{\rm b}(t)-E]\,... ...er p-1}\,\Theta[E-E_{\rm b}(t)]\,\left[{E\over E_{\rm b}(t)}-1\right]^{-(p+1)}.$$ (12)

Admittedly, the process of acceleration that we have discussed is not well understood, our derivation is heuristic and Eq. (12) is not even a continuous function (the step function in Eq. (9) should not be so abrupt, the magnetic energy in Eq. (10) should not have a fixed value). All we want to conclude from this exercise is that, when the probability of an electron to have been ``kicked'' only once is not negligible (A₁ comparable to A₂), the electron spectrum has an injection bend at $E\sim E_{\rm b}(t)$, around which its spectral index changes by $\sim$1 from $\sim$2 to $\sim$p+1. We choose to characterize this behaviour by the function:

$${{\rm d}n_{e}\over {\rm d}E} \propto {E^{-2}\over \sqrt{1 + [E/E_{\rm b}(t)]^{2\,(p-1)}}}\cdot$$ (13)

Note how similar the injection bend is to a cooling break (also a spectral steepening by roughly one unit) even though their origins are so different. The observational evidence for an injection bend at the injection energy turns out to be strong, as we proceed to show.

4 Evidence for an injection bend

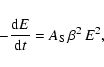
The injection bend induces the gradual transition in the spectral energy distribution described by Eq. (4), occurring at a ``bend'' frequency:

$$\nu_{\rm b} \simeq {1.87\times 10^{15} \over 1+z}\, {[\gamma... ...\, \left[{n_p\over 10^{-3}\;{\rm cm}^3}\right]^{1/2} {\rm Hz},$$ (14)

where we have used the characteristic synchrotron frequency of Eq. (3) for the magnetic field of Eq. (2), and transposed the result to the observer's frame.

For the reference CB parameters and z=1, $\rm\nu_b(t=0)\simeq 0.93\times 10^{15}$ Hz, above the optical band. Since the product $\gamma^3\, \delta$ typically declines by more than an order of magnitude within a couple of days, the bend frequency in many GRBs crosses the optical band into the NIR during the early afterglow. In Fig. 2 we present the time dependence of $\nu_{\rm b}(t)$ for $\gamma _0=1250$ and 750, characterizing the range of the observations, for various angles $\theta$, z=1, and the rest of the parameters at their reference values of Table 1. The figures show that, depending on the parameters, the bend frequency in the early AG may be above or below the optical band, and, if it is above, it will cross it later.

	Figure 2: Typical predictions for the bend frequency in the AG spectrum as a function of time, for $\theta =0,\,3/\gamma _0$and $10/\gamma _0$. The ``optical'' U to I band is shown as a horizontal band. Upper panel: for $\gamma _0=1250$. Lower panel: for $\gamma _0=750$.
Open with DEXTER

The bend frequency of the CB model is not the break frequency of the traditional fireball model. The time evolution of the former is given by Eq. (14), and is different from that of the latter, which, prior to the ``break'' in the AG light-curve, can be shown to be t^-1/2 (Granot & Sari 2002).

The evolution predicted by Eq. (4) from a  $\nu^{-0.5\pm 0.1}$ to a  $\nu^{-1.1\pm 0.1}$ spectral behaviour is affected by extinction. The early behaviour corresponds to times when CBs are not yet very far from their progenitors: extinction in the host galaxy may steepen the spectrum. After a day or more, when the CBs are further away, we do not expect strong extinction in the host. So the prediction (after extinction in the Galaxy is corrected for) is an evolution from a behaviour close to - or steeper than -  $\nu^{-0.5\pm 0.1}$, to a more universal $\nu^{-1.1\pm 0.1}$ at later times.

The predicted spectral behaviour has been observed, with varying degrees of significance, in the AG of several GRBs, listed in Table 2. The first column is the bend frequency $\rm\nu_b^0$ at t=0, computed with Eq. (14) and the optical AG parameters of Table 3 (the density n_p is extracted from the measured $x_\infty$ with use of Eq. (38) and our reference $R_{\rm max}$ and $N_{_{\rm CB}}$). For the listed GRBs the bend frequency is above the visible band at t=0 and the early AG measurements result in effective spectral slopes, $\beta(t_1)$, not far from the expectation $-0.5\pm 0.1$, or somewhat steeper. A few days later, the measured values, $\beta(t_2)$, are compatible with the expectation ${-1.1\pm 0.1}$. The second entry on GRB 990510 in Table 2 (Beuermann et al. 1999) requires an explanation. These authors argue that $\beta(t_2)=0.55\pm 0.10$, a result that assumes a strong extinction correction in the host galaxy. But, after a day or so, we do not expect such an extinction. For the latest points measured by Beuermann et al. (1999), at day 3.85 (well after the bend), $B-R=0.98\pm 0.07$and $R-I=0.49 \pm 0.06$. Converting these results - without extinction - to a spectral slope yields $\beta(t_1)=1.11\pm 0.12$, in agreement with expectation.

 

Table 2: The crossing of the bend frequency through the U to I bands [(10 to 3) $\times 10^{15}$ Hz]^b.

 

Table 3: The afterglow parameters^c.

 

Table 4: Frequencies, in GHz, at which the radio AGs of GRBs of known redshift were measured^d.

^d

References:
GRB 970508: Frail et al. (2000a).
GRB 980425: Kulkarni et al. (1998).
GRB 990123: Kulkarni et al. (1999b); Galama et al. (1999).
GRB 990510: Harrison et al. (1999).
GRB 991208: Galama et al. (2000).
GRB 991216: Frail et al. (2000b).
GRB 000301c: Berger et al. (2000).
GRB 000418: Berger et al. (2001a).
GRB 000926: Harrison et al. (2001).

The evolution from a softer to a harder spectrum should be a gradual change in time, rather than a sharp break, so that an AG's optical spectrum, if ``caught'' as the injection bend is ``passing'' should have an index evolving from $-0.5\pm 0.1$ to ${-1.1\pm 0.1}$ with the time dependence described by Eqs. (4) and (14). In Fig. 3 we test this prediction in the case of GRB 970508, for the time-dependent value of the ``effective'' slope $\alpha \simeq \, \Delta\, [\log\, F_\nu]/\Delta\,[\log\,\nu]$, constructed from the theoretical expectation in the same frequency intervals used by the observers. The actual predicted $\nu_{\rm b}(t)$ in Eq. (14) is obtained by use of the optical-AG fitted parameters ($\theta$, $\rm\gamma_0$ and $x_\infty$) that determine $\gamma(t)$ and $\delta(t)$, and the density n_p deduced from $x_\infty$ and the reference $N_{_{\rm CB}}$ and $R_{\rm max}$. The data are gathered by Galama et al. (1998a) from observations in the U, B, V, $R_{\rm c}$ and $I_{\rm c}$ bands (Castro-Tirado et al. 1998; Galama et al. 1998b; Metzger et al. 1997; Sokolov et al. 1998; Zharikov et al. 1998), by Chary et al. (1998) for K band results, and by Pian et al. (1998) for the H band.

Figure 3: A comparison between the predicted evolution in time of the effective spectral slope through the optical/NIR band and the data collected by Galama et al. (1998a) for the U, B, V, $R_{\rm c}$ $I_{\rm c}$ band of the AG of GRB 970508 (upper panel), for the K and $R_{\rm c}$ band (full squares, lower panel, Chary et al. 1998) and for the H and $R_{\rm c}$ band (triangle, lower panel, Pian et al. 1998) The three coloured lines, in the same order, are the (parameter-less) predictions.

Open with DEXTER

In spite of considerable uncertainties in the spectral slopes deduced from observations (Galama et al. 1998a), the results shown in Fig. 3 are satisfactory: the observed crossing of the injection bend is in agreement with the theoretical prediction, based on the fit in DDD 2001 to the overall R-band light curve from which the GRB 970508 AG parameters have been fixed; no extra parameters have been fit. A couple of points in the lower panel do not agree with the prediction, but they do not agree with the observations at very nearby frequencies reported in the upper panel, either.

A complementary analysis to that in the previous paragraph is the study of an AG's optical spectrum at a fixed time at which the injection bend is crossing the observed frequency range, or is nearby. A spectral ``snapshot'' at such time should have the intermediate slope and curvature described by Eq. (4) for $\rm\nu\sim\nu_b$. To test this prognosis, we compare in Fig. 4 the predicted spectral shape of the optical/NIR AG of GRB 000301c around March 4.45 UT ($\sim$3 days after burst) to its measured shape (Jensen et al. 2001). We have selected this GRB because its extinction correction in the galactic ISM is rather small: E(B - V)=0.05 (Schlegel et al. 1998), and there is no evidence for significant extinction in the host galaxy (Jensen et al. 2001). The theoretical line in Fig. 4 is given by Eq. (4) with the observer's $\rm\nu_b$of Eq. (14) ( $\nu_{\rm b}\,(1+z)=1.75\times 10^{14}$ Hz at t=3 days, for the density deduced from the value of $x_\infty$of this GRB, and the reference values of $N_{_{\rm CB}}$ and $R_{\rm max}$). In the figure the theory's normalization is arbitrary but the (slightly evolving) slope of the theoretical curve is an absolute prediction: it is based on the fit in DDD 2001 to the overall R-band light curve and, once more, no extra parameters have been fit. The result is astonishingly good, even for the curvature which - given the figure's aspect ratio as chosen by the observers - is not easily visualized (a look at a slant angle helps). The late-time spectral slope deduced from the HST observations (Smette et al. 2001) around day 33.5 after burst indicated a slope of $\sim$-1.1, again in agreement with our expectation.

	Figure 4: Comparison between the observations and the (parameter-less) prediction for the spectral shape of the optical AG of GRB 000301c, at $\sim$3 days after burst. Data from Jensen et al. (2001).
Open with DEXTER

We conclude that the evidence is very strong for a spectral injection bend at the time-dependent frequency, Eq. (14), predicted in the CB model. As illustrated in Fig. 1 and contrasted with data in Sect. 8, further evidence for the injection bend is provided by the fact that it is essential to the description of the observed broad-band spectra of GRB afterglows.

5 The cumulation factor

Three factors that are irrelevant in the optical and X-ray domains play a role in the description of the longer radio wavelengths and the early radio AG. In this section we discuss the first one of them.

Electrons that enter a CB with an injection Lorentz factor $\gamma(t)$are rapidly Fermi accelerated to a distribution that we have argued to be roughly that of Eq. (9). On a longer time scale, they lose energy by synchrotron radiation, and their energy distribution evolves as in Eq. (11). Electrons with a large $\gamma\sim {\cal{O}}\,[\gamma(t)]$ emit synchrotron radiation, with no significant time-delay, at the observer's optical and X-ray wavelengths. But the emission of radio is delayed by the time it takes the electrons to ``descend'' to an energy at which their characteristic emission is in the observer's radio band. At the start of the afterglow, when equilibrium conditions have not yet been reached, this implies a dearth of radio emission relative to the higher-frequency bands. This introduces a ``cumulation factor'' ${\rm C}(\nu,t)$ in Eq. (6).

Consider a fixed observed radio frequency $\nu_{\rm obs}$. It corresponds to a time changing frequency $\nu=(1+z)\nu_{\rm obs}/\delta(t)$ in the CB system. The CB electrons preferentially emitting at this frequency (over an unconstrained range of pitch angles) are those whose Lorentz factor $\rm\gamma_e$ satisfies the relation $\rm\nu \sim 0.22\,\gamma_e^2\,\nu_L$, in analogy to Eq. (3). To estimate the time $\rm\Delta t$ it takes an electron to decelerate from $\gamma\sim \gamma(t)$ to $\rm\gamma=\gamma_e$, substitute the magnetic energy density of Eq. (1) into the electron energy loss of Eq. (10) and integrate, to obtain

 

$$\Delta t {3\,m_{e}\over n_{p}\,m_{p}\,\sigma_T\,c}\,{1\over\gamma^2}\, \left({1\over \gamma_{\rm e}}-{1\over \gamma}\right)$$ =

$$[8.27\times 10^7\,{\rm s}]\left[{{10^{-3}\,{\rm cm}^{-3}}\over{n_... ...10^6\over \gamma^2}\, \left({1\over \gamma_{\rm e}}-{1\over \gamma}\right)\cdot$$ = (15)

The function $\gamma$ is given by Eq. (37) of Appendix A, which we may rewrite as:

$${1\over \gamma^2} = {1\over \gamma_0^2}\left[1+{t\over t_0}\right]$$

$$t_0\equiv [5.14\times 10^7\, {\rm s}] \left[{x_\infty\over 1\;{\rm Mpc}}\right] \left[{10^3\over \gamma_0}\right]^2.$$ (16)

The electrons emitting the observed radio frequencies have $\rm\gamma_e\!\sim\! {\cal{O}}(1)$, so that the proper CB times $\Delta t$ and t₀ are of ${\cal{O}}(1)$ year, corresponding to observer's times - foreshortened by a factor $(1+z)/\delta$ - of ${\cal{O}}(1)$ day. For optical and radio observations $\gamma_{\rm e}\!\sim\! {\cal{O}}(\gamma)$there is no significant delay in their emission. Moreover, the electron accumulation rate ( $\eta \pi\,R_{\rm max}^2\,n_{e}\,c\,\gamma$ in the CB system) is orders of magnitude larger than the characteristic synchrotron cooling time $E/({\rm d}E/{\rm d}t)$ of Eq. (10), even for $\gamma\sim 10^3$. Thus, the optical and X-ray AG emission starts as soon as the CB is transparent to its enclosed radiation: for each CB, a few observer's seconds after the corresponding $\gamma$-ray pulse (DDD 2001). The radio signal, on the other hand, must await a time $\Delta t$ for the cumulated electrons to cool down.

The simple way to parametrize the frequency-dependent ``cumulation effect'' is to use the expression for the total number of electrons N(t) incorporated by the CB up to time t (Eq. (40) of Appendix A) and to posit:

$$C(\nu,t)={N(t-\Delta t)\over N(t)}\,\Theta(t-\Delta t),$$ (17)

where the frequency dependence is via $\Delta t=\Delta t(\nu,t)$, and the sharp start at $t>\Delta t$ is an artifact of our simplifications. For optical and X-ray frequencies, $\Delta t=0$ and $C(\nu,t)=1$. In practice we find that, except for GRB 980425 whose viewing angle is exceptionally large, one may also use within the radio band an approximation to Eq. (17):

$$C(\nu,t)\sim C(t)=\left[1-{\gamma(t)\over\gamma_0}\right]^{1/2},$$ (18)

which is also frequency independent.

6 The attenuation factor

At optical and X-ray frequencies the CB is transparent and, for the spectrum of Eq. (4), the bulk of the radiation's energy is emitted around the bend frequency $\rm\nu_b$. At such relatively high frequencies, as illustrated in Fig. 1, absorption is unimportant. Thus, for optical and X-ray afterglows (DDD 2001) it suffices to know that all of the incoming electron's energy is reradiated, the spatial distribution of the radiating electrons within the CB is irrelevant. But in the radio, where absorption is important, the location of these electrons inevitably plays a role. In the next sections we argue that it is plausible that the radiating electrons be close to the surface ``illuminated'' by the ISM (Sect. 6.1), and that the values of the CB's plasma frequency (Sect. 6.2) and free-free absorption coefficient (Sect. 6.3) actually suggest that they may be relatively close to that surface. In Sect. 6.4 we deduce the final form of the attenuation factor in the CB model, characterized by a single parameter.

6.1 Electron penetration

Using numerical simulations, Achterberg al. (2001) have shown that for simple geometries the bulk of highly relativistic particles encountering a collisionless shock escape before they undergo diffusive shock acceleration. In reality, the geometry of the CB, its density distribution and its magnetic field distribution are very complicated, making the fraction of the ISM electrons that penetrate inside the CB, and their distribution there, very uncertain.

Several length scales play a role in discussing the fate of an electron that enters the CB with $\gamma_{\rm e}=\gamma(t)$. The Larmor radius is $R_{\rm L}=m_{e}\,c^2\,\gamma/\rm (e\,B)$, which is independent of $\gamma$ for B scaling as in Eq. (2). For our reference parameters, $R_{\rm L}\sim 6$ km is many orders of magnitude smaller than the CB's radius and does not play a crucial role. The length of an electron's curled-up trajectory as it radiatively loses energy is $c\,E/({\rm d}E/{\rm d}t)$ or $\sim$ $2.6\times 10^{15}$ cm for the cooling rate of Eq. (10) and an initial $\gamma=10^3$. This is only an order of magnitude larger than the reference CB's radius $R_{\rm max}$. We have no way to estimate the typical coherence size of a CB's magnetic domain $L_{\rm B}$, but the depth $D\sim (c\,\tau_\gamma\;L_{\rm B})^{1/2}$ to which an electron penetrates, even for a relatively simple magnetic mess ($L_{\rm B}$ not much smaller than $R_{\rm max}$) is smaller than the CB's radius. For $L_{\rm B}$ as small as $R_{\rm L}$, $D\sim 4\times 10^{10}$ cm, some four orders of magnitude smaller than $R_{\rm max}$. Even this concrete value is uncertain, for it depends on the surface magnetic field as B^-3/4, and the surface B-value may be different from that of Eq. (2), which is a volume average.

In addition to all of the above uncertainties, it is possible that a CB's illuminated working surface be turbulent, and harbour fast plasma motions, if only to establish local charge neutrality, which is disrupted as electrons and protons penetrate the CB to different depths. We conclude that the the fraction of ISM electrons that enter inside the CB may be small and the synchrotron-radiating electrons may be concentrated close to the CB's surface, as opposed to be acquiring a uniform distribution over the CB's volume.

6.2 The plasma frequency

The plasma frequency in a CB with an average free inner electron density $\bar n_e^{\rm free}$ is:

$$\nu_{p} = \left[{\bar n_{e}^{\rm free}\, e^2\over\pi\, m_{e}}... ...{\rm free}\over 10^7\;{\rm cm}^{-3}}\right]^{1/2}\, {\rm MHz}.$$ (19)

For a fully ionized CB $\bar n_{e}^{\rm free}=\bar n_{e}$, to whose reference value we normalized the above result (the fraction of electrons swept up from the ISM is small, relative to the total number in the CB - to whose free fraction Eq. (19) refers - but the CB is highly ionized, as shown in Appendix C).

For $\nu\!<\!\nu_{p}$the radio emission is completely damped within a typical length $\sim c/[\nu_p^2-\nu^2]^{1/2}$, much smaller than the CB's radius. At very early times, $\delta\sim 10^3$ and the Doppler-boosted value of $\nu_p$ falls in the low end of the observed range of radio signals, where a sharp cutoff is not observed. We must conclude that the (small fraction of) radiating electrons is located in a CB surface layer whose total electron density (dominated by the thermal electron constituency) is smaller than our reference average value, a one order of magnitude reduction being comfortably sufficient to move the value of $\nu_p$ to a position below the currently observed frequencies. We have explicitly checked that our fits do not improve significantly with the inclusion of $\nu_p$ as a free parameter: the minimization procedure always ``gets rid'' of the fit $\nu_p$ by choosing it somewhat below the reference value of Eq. (19), and below the lowest measured frequencies.

6.3 Free-free attenuation

At the MHz frequencies in the CB system corresponding to the observed radio frequencies, the synchrotron emission is strongly attenuated by free-free absorption (inverse bremsstrahlung) in the CB; free-free absorption dominates over self-synchrotron absorption, as shown in Appendix D. For a hydrogenic plasma, the free-free absorption coefficient at radio frequencies is:

$$\chi_\nu \simeq 0.018\, g_{\rm ff}\,\bar n_{e}\, \bar n_{i}\, T^{-3/2}\, \nu^{-2}\, {\rm cm}^{-1}\, ,$$ (20)

where $\bar n_{i}\simeq \bar n_{e}$ is the free ion density in the CB, in units of cm^-3, T is the plasma temperature in degrees Kelvin, $\nu$ is in Hertz and  $g_{\rm ff}$ is a Gaunt factor for free-free emission, of $\cal {O}$(10) at the relevant frequencies.

The opacity $\tau_\nu$ of a surface layer of depth D is:

$$\tau_\nu(D,t) =\int_{R_{\rm max}-D}^{R_{\rm max}}\chi_\nu \, {\rm d}r\equiv \bar \chi_\nu[t]\,D.$$ (21)

Equilibrium between photoionization of atomic hydrogen in the CB by synchrotron radiation and recombination of free electrons and protons to hydrogen keeps the CB plasma partially ionized during the observed AG. The Coulomb relaxation rate in the CB is very fast because of its high density. Consequently, the CB plasma is approximately in quasi thermal equilibrium. Because of the exponential dependence of the Saha equation on temperature, and the high ionization rate, the CB's temperature is kept practically constant around a few eV, and the ion density and free electron density become proportional to $\gamma(t)$ (Appendix C). Using T₀= 10⁵K and the reference average densities $\bar n_{e}=\bar n_i\simeq 10^7\, \rm cm^{-3}$ in Eqs. (20) and (21), we obtain:

$$\tau_\nu(D,t)\sim 1.4\times 10^2 \left[{D\over R_{\rm max}}\r... ...~GHz}\over \nu}\right]^2 \, \left[{T\over 10^5}\right]^{-3/2},$$ (22)

which is very large for $D\sim {\cal{O}}(R_{\rm max})$. A reduction in surface or average CB density of one order of magnitude or more - which, as we have seen, renders unobservable the unobserved plasma-frequency cutoff - reduces $\tau_\nu$ by two orders of magnitude, or more. For $D\sim R_{\rm max}/10$, this would make $\tau(D)$, as required, of order unity at the peak frequency $\sim$10² GHz of the early-time spectrum of Fig. 1 (at which time the observed and CB frequencies differ by a factor $\delta/(1+z)\sim 10^3$).

The conclusion is that a reasonable deviation of the properties of the CB from their reference bulk average values (a reduction of the total number-density of free electrons in a synchrotron-emitting surface layer) implies, not only that the plasma-frequency break is not observable in the current data, but also that the magnitude of the free-free attenuation is the required one. Our ignorance of the depth, temperature and density of ions and electrons in the radio-emitting surface of a CB can be absorbed into a single parameter: a characteristic absorption frequency, $\rm\nu_a$, in the opacity of Eqs. (20)-(22):

$$\tau_\nu\equiv\left[{\nu\over\nu_a}\right]^{-2}\,\left[{\gamma(t)\over \gamma_0}\right]^{2}\cdot$$ (23)

The frequency dependence of the free-free attenuation, $\chi_\nu\propto\nu^{-2}$, is fairly well supported by the observed radio spectra at their lowest frequencies, as our comparisons with observations in Sects. 8 and 9 demonstrate.

6.4 Attenuation in slabs and spheres

We do not know a priori the geometry of the working surface from which a CB's synchrotron radiation is emitted. In the case of optical AGs this is immaterial, for the CB is transparent to radiation at the corresponding CB-system wavelengths: the bulk of the radiation energy is emitted at these frequencies. For the case of radio AGs, attenuation is important and the shape of the emitting surface layers plays a role: the expression for attenuation as a function of opacity is geometry-dependent.

For a planar-slab geometry, the familiar expression for the attenuation is:

$$\rm {\it A}[\nu]={1-e^{-\tau_\nu}\over \tau_\nu}\cdot$$ (24)

For the emission from a sphere of constant properties, we obtain:

$$\rm {\it A}[\nu]= {3\, \tau_\nu^2-6\, \tau_\nu+6\, [1-e^{-\tau_\nu}]\over \tau_\nu^3}\, ,$$ (25)

while for the emission from a thin spherical surface, the result of Eq. (24) is recovered.

For the sake of definiteness, we adhere to CBs that are spherical in their rest system. This means that, as the frequencies increase and the CB evolves from being opaque to being transparent, we should use an attenuation evolving from Eq. (25) to Eq. (24). Rather than doing that, we have checked explicitly that our results are insensitive to the use of one or the other form, and used the simpler one.

7 The illumination and limb-darkening factor

Consider a spherical CB in its rest system. It is ``illuminated'' by incoming ISM electrons only in its ``front'' hemisphere. If observed at an angle $\rm\theta_{_{CB}}\neq 0$, a fraction of the ``dark'' CB is also exposed to the observer, like the Moon in phases other than totality. For radio waves - to which the CB is not transparent - these geometrical facts play a non-trivial role.

Place the direction of the CB motion, or of its illumination, at $(\theta,\phi)=(0,0)$; at a direction $\rm\vec n_i=(0,0,1)$ in Cartesian coordinates. The normal to a sphere's surface point at $(\theta,\phi)$is $\rm\vec n_s=(\cos\theta\sin\phi,\sin\theta,\cos\theta\cos\phi)$. The observer is in the direction $\rm (0,\theta_{_{CB}})$, where we have taken the liberty to label ``$\theta$'' what in this parametrization is an azimuthal angle; the corresponding unit vector is $\rm\vec n_{_{CB}}=(\sin\theta_{_{CB}},0,\cos\theta_{_{CB}})$. The relation between $\rm\theta_{_{CB}}$ and the terrestrial observer's viewing angle is that of Eq. (7).

When attenuation plays a significant role, an element of a CB's surface reemits an amount of energy proportional to the cosine of the illumination angle: $\rm\vec n_i \cdot \vec n_s$. Because of the limb-darkening effect, the reemitted radiation depends on the cosine of the angle between the surface element and the observer: $\rm\vec n_s \cdot \vec n_{_{CB}}\equiv \mu$. A simple characterization of the functional form of the limb darkening effect (see e.g. Shu 1991) is:

$$F(\mu)=\left({2\over 5}+{3\over 5}\,\mu\right)\,\Theta[\mu].$$ (26)

The combined effect of illumination and limb darkening is an emitted radiation proportional to:

 

$$E(\cos\theta_{_{\rm CB}}) \int^1_{-1} {\rm d}\cos\theta\int^{\pi/2}_{\theta_{_{\rm CB}}-{\p... ...(\vec n_{\rm s} \cdot \vec n_{_{\rm CB}})\, \vec n_{\rm i} \cdot \vec n_{\rm s}$$ =

$${1\over 5}\,\left[2+(2+\pi-\theta_{_{\rm CB}})\cos\theta_{_{\rm CB}} +\sin\theta_{_{\rm CB}}\right].$$ = (27)

An excellent and simple approximation to Eq. (27) is:

$$E(x)=E(1)\,{1\over 10}\, [4+x][1+x],$$ (28)

with $x=\cos\theta_{_{\rm CB}}$.

For negligible self-attenuation $A[\nu]=1$, as in the optical, there is no limb darkening and illumination effect. As absorption becomes increasingly important for longer wavelengths, the effect becomes fully relevant. We interpolate between these two extremes by writing:

$$L_{_{\rm CB}}(\nu,\cos\theta_{_{\rm CB}})\simeq A[\nu]+(1-A[\nu])\, {E(\cos\theta_{_{\rm CB}})\over E(1)}$$ (29)

to obtain the overall illumination and limb-darkening correction factor to the energy flux density of Eq. (6).

8 Broad band spectra: Radio and optical results

In practice, it is not an effortless task to test a prediction for an AG's spectrum extending, as in the upper panel of Fig. 1, to all measured wavelengths from radio to X-rays. The problem is not related to the model, but to the data. First, the corrections due to absorption, particularly in the host galaxy, are frequency-dependent and notoriously difficult to ascertain with confidence. Second, the integration times employed in the radio observations are long, so that the theoretical prediction varies within the time window, and so do the optical energy flux densities, measured over much shorter periods, as well as some of the radio observations themselves. Unavoidably, this will make our spectral figures look a bit peculiar, with two theoretical curves bracketing the expectations, and various observational points at the same frequency.

We study the AG light-curves and broad-band spectra of all GRBs with known-redshift whose AG was measured both in the radio and optical bands.

Our predictions are given by Eq. (8), fit to the optical and radio observations. The fitted parameters are the overall normalization, $\gamma(0)$, $\theta$, the deceleration parameter $x_\infty$ (whose meaning and role are reviewed in Appendix A) and the CB self absorption frequency $\rm\nu_a$ of Eq. (23). We found in DDD 2001 that p is very narrowly distributed around its theoretical value p=2.2, and we fix it to that value for all GRBs in the current analysis. Thus, the total number of parameters in our broad-band fits is the same as we used in DDD 2001 to describe just the R-band light-curve.

The values of the parameters, listed in Table 3, are very similar to those deduced in DDD 2001 by fitting only the R-band optical data with the high-$\nu$ limit of Eq. (8). The small differences are due not only to the use of radio data and optical bands other than R, but also to the inclusion of the effects of the injection bend in the CB synchrotron AG global formula, Eq. (8), and (to a small extent) to the use of a fixed p=2.2. The results show that the theory agrees with observations both at radio and optical wavelengths. For some GRBs a slightly better fit to the radio data is obtained if the absorption frequency $\rm\nu_a$ is best fitted to the radio data alone or if a fitted power-law dependence on time is used for the CB opacity instead of Eq. (23), with all other parameters taken from the global fit. Because of scintillations, and of the very detail-dependent character of our prediction for the time dependence of a CB's opacity, it is difficult to assess whether or not the slightly improved $\chi^2$ values are significant or not.

Notice in Table 3 that the distributions of parameters are fairly narrow, in particular for $\gamma_0$. Of particular interest, since it can be predicted, is the distribution in $\gamma \times\theta$. Since AGs are discovered at optical and X-ray frequencies, the angular distribution is that of the high frequency limit of Eq. (8). For small $\theta$, ${\rm d}\,N/{\rm d}\theta\propto \theta/(1+\gamma^2\theta^2)^{4.1}$. This distribution has a maximum at $\gamma\theta\sim 0.37$and a median at $\sim$0.5. In Table 3 there are four cases with $\gamma\theta$ below the median and five above. The worst ``outlier'' in $\theta$ is much less so in $\gamma\theta$. The conclusion that this distribution is perfectly compatible with the expectation can also be reached from Fig. 39 of DDD 2001, whose results were obtained from only optical data, but for which the statistics is a bit better.

We first discuss the broad-band spectra and light curves of three representative GRBs: 000301c, 000926 and 991216. The optical AG of GRB 000301c is practically unextinct, that of GRB 000926 has strong extinction in the host galaxy (e.g., Fynbo et al. 2001) and that of GRB 991216 has strong extinction both in the host galaxy and in ours (e.g., Halpern et al. 2000). We discuss GRBs 991208, 000418, 000510, 990123 and 970508 in slightly less detail. The apparently special case of GRB 980425 is discussed separately in the next chapter.

8.1 GRB 000301c

For this GRB we fit the radio data of Berger et al. (2000) and the optical data of Garnavich et al. (2000b), Jensen et al. (2001), Masetti et al. (2000), Rhoads & Fruchter (2001) and Sagar et al. (2001). Our results for the light curves at all observed optical and radio frequencies are gathered in Fig. 5, which is representative of the trends seen in all GRBs. The narrowly spaced lines in the figure are the optical light curves for - from top to bottom - the K, J, I, R, V, B and U bands. Their very satisfactory comparison with data is reported in Fig. 6. The results for the radio AG are the more spaced lines in Fig. 5, which correspond - from top to bottom at the figure's left side - to frequencies of 1.43, 4.86, 8.46, 15, 22.5, 100, 250 and 350 GHz. Their very satisfactory comparison with observations is reported in Figs. 7 to 10. Notice that all features of the data have precisely the trends summarized in Fig. 5. In Figs. 11 and 12 we present the complementary information, by comparing our fits with the observations for the radio-to-optical spectra of GRB 000301c in four radio time-integration brackets; 1 to 5, 5 to 10, 10 to 20, and 20 to 30 days. The pronounced peaks are at (observer's) frequencies for which the opacity of Eq. (23) is $\rm\tau_\nu\sim{\cal{O}}(1)$. The injection bend at a higher frequency is clearly visible, it is responsible for the agreement between the radio and optical magnitudes and frequency trends. The two curves in these figures, and many later ones, refer to the expectation at the two times which bracket the actual radio observation. The results are quite satisfactory.

	Figure 5: Results of a fit to radio and optical observations of the light curves of GRB 000301c. The narrowly spaced lines refer - from top to bottom - to the K, J, I, R, V, B and U bands. The more widely spaced lines refer - from top to bottom at the figure's left side - to frequencies of 1.43, 4.86, 8.46, 15, 22.5, 100, 250 and 350 GHz. The comparison with data is shown in Figs. 6 to 12.
Open with DEXTER

8.2 GRB 000926

We have made a global fit to the NIR/optical data (Di Paola et al. 2000; Fynbo et al. 2001, Harrison et al. 2001; Price et al. 2001; Sagar et al. 2001) and the radio data (Harrison et al. 2001) on this GRB. In Fig. 13 we compare the fitted CB-model predictions with the measured light curves for the I, R, V, B and U bands, after subtraction of the host galaxy and SN contributions (DDD 2001). The theoretical predictions were corrected for galactic extinction E(B - V)=0.0235 (Schlegel et al. 1998) and for the estimated extinction in the host galaxy, E(B - V)=0.40 (Harrison et al. 2001). In Figs. 14 to 16 we present the radio light curves for six frequencies ranging from 98.48 to 1.43 GHz.

In Figs. 17 to 19 we make the complementary comparison of theory and observations for the radio-to-optical spectra, in six time intervals extending from 0.8 to 100 days. The results, in spite of the crude estimate of extinction in the host galaxy and the scintillations so clearly visible in the radio light curves, are satisfactory.

8.3 GRB 991216

The NIR/optical data for this GRB are from Halpern et al. (2000) and Garnavich et al. (2000a); the radio data from Frail et al. (2000b). In Fig. 20 we present the comparison between the measured light curves for the K, J, I, R bands, after subtraction of the host galaxy and SN contributions (DDD 2001), and the fitted CB model predictions. The predictions were corrected for extinction in the host galaxy and ours, as estimated by Halpern et al. (2000): E(B - V)=0.40. In Figs. 21 to 23 we present the radio light curves at six frequencies from 350 to 1.43 GHz. In Figs. 24 to 26 we make the complementary comparison of theory and observations for the radio to optical spectra, in six time intervals extending from 0.44 to 80 days. The results are once again satisfactory.

8.4 GRB 991208

We fit the NIR/optical data (Castro-Tirado et al. 2001; Sagar et al. 2000) and the radio data (Galama et al. 2000) on the AG of GRB 991208. In Fig. 27 we present the comparison between the measured light curves for the I, R, V and B bands, and the fitted CB model predictions, after subtraction of the host galaxy and SN contributions (DDD 2001). The theoretical predictions were corrected only for the small galactic extinction E(B - V)=0.016 (Schlegel et al. 1998) in the direction of this GRB, there being no spectral evidence for optical extinction in the host galaxy. In Figs. 28 to 31 we also present the radio light curves at 100, 86.14, 30, 22.49, 14.97, 8.46, 4.86 and 1.43 GHz. In Figs. 32 and 33 we make the complementary comparison for the radio to optical spectra in three time intervals extending from 2 to 14.3 days. The results are satisfactory.

8.5 GRB 000418

The NIR/optical data are from Klose et al. (2000) and the radio data from Berger et al. (2001a). In Fig. 34 we compare the fitted CB-model predictions with the measured light curves for the R-band, after subtraction of the host galaxy and SN contribution (DDD 2001). The theoretical predictions were corrected for galactic extinction and for extinction in the host galaxy as estimated by Berger et al. (2001a): E(B - V)=0.40. In Figs. 35 and 36 we also present the radio light curves at 22.5, 15, 8.46 and 4.86 GHz. In Fig. 37 we make the complementary comparison for the radio to optical spectra, in two time intervals extending from 9.5 to 100 days. The results are satisfactory.

8.6 GRB 990510

The NIR/optical data were gathered by Beuermann et al. (1999), Harrison et al. (1999) and Stanek et al. (1999) and the radio data by Harrison et al. (1999). In Fig. 38 we present the comparison between the measured light curves for the I, R, V, B bands, after subtraction of the host galaxy and SN contribution (DDD 2001), and the fitted CB model predictions, corrected for Galactic extinction ( E(B - V)=0.203, Schlegel et al. 1998) and for extinction in the host galaxy as estimated by Stanek et al. (1999). In Figs. 39 and 40 we present the radio light curves at 13.7, 8.6 and 4.8 GHz. In Figs. 40 and 41 we also make the complementary comparison of theory and observations for the radio to optical spectra three time intervals extending from 1 to 40 days. The agreement between theory and observations is very good although its significance is limited by the sparse radio data.

8.7 GRB 990123

We have fit the NIR/optical data (Castro Tirado 1999; Fruchter et al. 1999; Galama et al. 1999; Holland et al. 2000; Kulkarni et al. 1999a) and the radio data (Galama et al. 1999; Kulkarni et al. 1999b) for this GRB. In Fig. 42 we present the comparison between the fitted CB model predictions - assuming a constant ISM density after 0.1 observer's days and after subtraction of the host galaxy and SN contributions - with the measured light curves for the K, I, R, V, B and U bands. The theoretical predictions were corrected for the small Galactic extinction in the GRB direction ( E(B - V)=0.016, Schlegel et al. 1998) but not for extinction in the host galaxy, since there is no spectral evidence for significant extinction there. In Fig. 43 we present the radio light curves at 15 and 8.46 GHz. In Figs. 44 to 45 we make the complementary comparison of theory and observations for the radio to optical spectra, in four time intervals extending from 0.1 to 20 days. The agreement between theory and observations is good despite the limited available data on the radio AG and its modulation by scintillations.

8.8 GRB 970508

The optical (and X-ray) AG of GRB 970508 is the only one so far that has been seen to rise and fall very significantly (e.g., Garcia et al. 1998; Galama et al. 1998b; Pedersen et al. 1998; Schaefer et al. 1997; Sokolov et al. 1998; Zharikov et al. 1998). In DDD 2001 we have shown that a CB model fit to this AG fails, if one assumes - like in all our other fits - a constant ISM density. However, we have argued there that GRB progenitors are presumably located in super-bubbles of 0.1 to 0.5 kpc size. There may be instances in which the jet of CBs, after travelling for such a distance, does not continue onwards to a similarly low-density halo region, but encounters a higher-density domain. Indeed, we have shown that a fairly satisfactory fit to the optical (and X-ray) AG is obtained upon assuming an upwards jump in density by a factor $\sim$2.2 at $t\sim 1.1$ day after burst. This jump occurs before the first available data points on the radio AG (Galama et al. 1998a; Frail et al. 2000b). Therefore, we have fitted the optical data and the radio data with the ISM density profile that was fitted to the R-band light curve.

In Fig. 46 we present the comparison between the measured light curve for the I, R, V and B bands after subtraction of the host galaxy and SN contribution (DDD 2001). The theoretical predictions were corrected for the small galactic extinction in the GRB direction ( E(B - V)=0.016, Schlegel et al. 1998) but not for extinction in the host galaxy, since there is no spectral evidence for significant extinction there. In Figs. 47 and 48 we also present the radio light curves at 8.46, 4.86 and 1.43 GHz. In Figs. 48 to 50 we make the complementary comparison of theory and observations for the radio to optical spectra, in five time intervals extending from 0.12 to 470 days. The results are quite satisfactory.

8.9 Commentary

In DDD 2001 we demonstrated that, in the CB model, the spectral index in the optical to X-ray domain could be extracted from the time-dependence of the optical light curves. The fits resulted in $\alpha=p/2\simeq 1.1$ for all GRBs of known redshift. This result is in good agreement with the observed late spectral observations. We have learned in this section that the CB model also provides an excellent description of the AG spectra in the broader band that includes the radio data. Only one new parameter, $\rm\nu_a$, is involved in the extension to the broader band. And this fitted parameter and the injection bend - at its predicted frequency and time-dependent position - bring about the agreement between the different magnitudes and spectral trends of the radio and optical domains.

In some of our fits to broad band spectra, such as the earliest data on GRBs 000301c, 991216 and 990123 in the upper panels of Figs. 11, 24 and 44, respectively, the theoretical curve is an underestimate of the low-energy spectral intensity. In other cases, such as GRBs 000926, 991208 and 980425, the spectral fits are excellent at all times. The lowest frequencies and earliest times are the most dependent on our simplifications concerning the GRB geometry, density profile, self-absorption, cumulation and limb-darkening. We would have been surprised if these simplifications worked even better than they do, and the fits do improve if we remove our approximation of a fixed spectral index p=2.2. But our aim in this paper is not to obtain spectacularly good fits, but to demonstrate that, even in the simplest approximations, the CB model provides a good description of the broad-band data. The analysis of the lowest radio frequencies at the earliest times brings forth a plethora of details that are not of fundamental interest: our ultimate goal is not to understand these details, but to investigate what the origin of GRBs actually is.

9 SN1998bw and GRB 980425

The time and position of the peculiar gamma ray burst 980425 (Soffita et al. 1998) coincided with supernova SN1999bw (Tinney et al. 1998) in the spiral galaxy ESO 184-G82, at a nearby z=0.0085 (Tinney et al. 1998; Sadler et al. 1998; Galama et al. 1998c; Lidman et al. 1998; Iwamoto et al. 1998). Iwamoto et al. (1998) estimated the the core collapse of SN1998bw to have happened within -2 to +7 days of GRB 980425. The BeppoSAX Narrow Field Instrument (NFI) located 10h after burst an X-ray source coincident in position with SN1999bw that declined slowly with time between April and November 1998 (Pian et al. 2000). A posteriori statistics indicate a very low chance probability ($\leq$10^-4) of a GRB being so nearly coincident in position. But despite how close - if it was associated with SN1999bw - the progenitor of GRB 980425 was to us (38 Mpc for $H=65\, \rm km\,Mpc^{-1}\, s^{-1}$), the $\gamma$-ray fluence indicated only $7\times 10^{48}$ erg equivalent spherical energy release in $\gamma$ rays, much smaller than $\sim$ $3\times 10^{53}$ erg, the mean value for the score of other GRBs with known - cosmological - redshifts.

9.1 SN1998bw: The accepted lore

Like its accompanying GRB, SN1998bw was also claimed to be a very peculiar radio supernova (e.g. Kulkarni et al. 1998). Over the past twenty years approximately two dozen SNe have been detected in the radio: 2 Type Ib, 5 Type Ic, and the rest Type II. A much larger list of more than 100 additional SNe have low radio upper limits (for a review see, e.g., Weiler et al. 2000 and references therein). Type Ib/c SNe are fairly homogeneous in their radio properties, but SN1998bw had a peak 6-cm radio luminosity of $\sim$ $\rm 8\times 10^{28}\, erg s^{-1} \, Hz^{-1}$, that is 20 to 40 times brighter than other radio Type Ib/c SNe, which fall typically in the range $\rm 1.4{-}2.6\, \times 10^{28}\, erg s^{-1} \, Hz^{-1}$. SN1998bw also reached a high radio luminosity earlier than any known SN. Simple arguments based on the brightness temperature of its radio luminosity (e.g., Readhead 1994) required the radiosphere of SN1998bw to have expanded surprisingly fast, at $\geq$ $\rm 200\,000\, km\, s^{-1}$, at least during the first few days. Its unusually high optical and radio luminosities and its extraordinarily large initial speed of expansion led many authors to conclude that SN1999bw was a hypernova (Paczynski 1998) rather than a peculiar supernova (e.g., Iwamoto et al. 1998).

9.2 The pair SN1998bw/GRB 980425 in the CB model

In Dar & De Rújula (2000a) we argued that the only peculiarity of SN1998bw was that it was viewed very near its axis. The peculiarity of GRB 980425 was its nearness, that allowed for its detection at an angle, $\theta\sim 8/\gamma(0)$ unusually large relative to the other GRBs of known redshift, for which $\theta\sim 1/\gamma_0$. These facts conspired to produce a ``normal'' GRB fluence, and resulted in an optical AG dominated by the SN. In DDD 2001, we demonstrated that the X-ray AG of this GRB was also ``normal'': it has precisely the light curve (in shape and normalization) expected in the CB model if the X rays are produced by the CBs and not, as the observers assume (Pian et al. 2000), by the supernova.

In the CB model (Dar & De Rújula 2000a), the gamma-ray fluence of GRBs at large viewing angle ( $\gamma_0^2\, \theta^2\gg 1$) is $\propto \delta_0^3\propto \theta^{-6}$. The radio AG spectral energy density is proportional to $\gamma^{1/2}\, \delta^{7/2}$, as implied by Eqs. (4), (6), (8), the dependence $\rm\nu_b\propto \gamma^3$ and the relation $\rm\nu_{obs}\propto\nu_{_{CB}}\,\delta$. As a function of time, the AG peaks when $\gamma\, \theta\sim 1$, so that $\gamma\simeq\delta\simeq 1/\theta$ and the peak value is proportional to $\theta^{-4}$. Because its proximity and large viewing angle ``conspired'' to make GRB 980425 appear ``normal'' in gamma rays, its peak radio intensity should have been enhanced by a factor $\sim$ $\rm (\theta/mrad)^2$ relative to that of ordinary GRBs. Thus, for $\theta\sim 8.3$mrad, as estimated for GRB 980425 in Dar & De Rújula (2001), its expected peak radio intensity is $\sim$60 times larger than that of ordinary GRBs. Observationally, it is 50 to 100 times larger.

In Figs. 51 to 55 we show our CB model fits to the temporal and spectral behaviour of the radio afterglow of GRB 980425. The fit parameters (in particular the large observation angle $\theta$) are quite close to the ones that explain its GRB fluence (Dar & De Rújula 2000a), and its X-ray afterglow (DDD 2001). These figures show how, in the CB model, the radio AG of GRB 980425 also has a ``normal'' magnitude and shape. That is, once more, if the radio AG is produced by the CBs and not by the SN, unlike, once again, it is generally assumed (e.g., Kulkarni et al. 1998; Li & Chevalier; Weiler et al. 2000).

In the case of GRB 980425 the relatively large viewing angle and the subsequently small Doppler factor imply that, at late times, even the radio frequencies are above the injection bend. The large $\nu$ behaviour in Figs. 53 to 55 is $\nu^{-p/2}\sim\nu^{-1.1}$. Also, the late time trend of the radio light curves in Figs. 51 and 52 approaches the asymptotic $t^{2(p+1)/3}\sim t^{-2.1}$.

For GRB 980425 the radio data are overwhelmingly more abundant and precise than the X-ray data, and it is interesting to check what the prediction for the X-ray light curve is, if the input parameters are those determined in the radio fits. This is done in Fig. 56 for two values of the electron spectral index p. For our fixed choice, p=2.2, the prediction misses the data by a factor $\sim$20. There are two excuses for that. First, since GRB 980425 is seen much more ``sideways'' than other GRBs, and its Doppler factor $\delta$ is much smaller than usual, the cumulation, illumination and limb-darkening factors play a bigger role than usual. These factors involve many simplifying assumptions (such as spherical symmetry) and significantly affect the normalization of the radio AG, but not that of the X-rays. Second, the extrapolation from radio to X-rays is over some 10 orders of magnitude in frequency, and a small change in the spectral photon's slope, (p - 1)/2, entails a very large change in relative magnitude, as can be seen in Fig. 56 by comparing the p=2.2 and p=2curves.

	Figure 56: The X-ray afterglow of GRB 980425.
Open with DEXTER

The X-ray light-curve of GRB 980245 is essentially flat in the time-interval of the first four observed points (Pian et al. 2000), while the corresponding data for all other GRBs fall with time much faster. The last observational point in Fig. 56, a preliminary result from XXM Newton (Pian 2002) and Chandra (Kouveliotou 2002), falls precisely in the expected subsequent fast decline (predicted in DDD 2001) and definitely not in a naive power-law extrapolation. The peculiar light curve is a consequence of the large observing angle (Dar & De Rújula 2000a). For the reasons stated in this paragraph and the preceding one, we consider the prediction of the X-ray fluence completely satisfactory.

In DDD 2001, on the basis of the very meager X-ray data, we argued that the last optically-measured point of the SN1998bw/GRB 980425 pair, at day 778 (Fynbo et al. 2000), was due to the CB's AG and not to the supernova. Redoing the analysis with the input of the abundant radio data, we must now revise this conclusion. In Fig. 55 we show the result, with inclusion of the late optical measurement. This point lies more than two orders of magnitude above the predicted CB's AG: it must be due to the SN. We do not have an explanation - specific to the CB-model - of the fact that this point also lies somewhat above the expectation based on $\rm ^{56}Co$ decay (Sollerman et al. 2000).

We are claiming that long duration GRBs are associated with a good fraction of core-collapse SNe. Yet, SN1998bw was one of the brightest in its class. The apparent contradiction may be dispelled by the increasing evidence that SN explosions are fairly asymmetric. It is quite conceivable that, viewed very close to their ``CB axis'' SNe appear to be brighter than when observed from other directions.

The conclusion is twofold. GRB 980425 is, in every respect, normal (z and $\theta$ being chance variables). And, deprived of very abnormal X-ray and radio outputs - which are not due to the supernova, but to its ancillary GRB - SN1998bw loses most of its ``peculiarity''.

9.3 Superluminal motion in SN1998bw/GRB 980425

The transverse projected velocity in the sky of a CB relative to its parent SN is, for large $\gamma$ and small $\theta$:

$$V_{_{\rm CB}}(t)\simeq {\gamma(t)\, \delta(t)\, \theta\over (1+z)}\; c\, ,$$ (30)

which, for typical parameters, is extremely superluminal. The resulting angular separation at time $\rm t$ is:

$$\Delta \alpha(t)={1\over D_A}\int_0^t\,V_{_{\rm CB}}(t')\;{\rm d}t',$$ (31)

where $D_A=(1+z)^2\, D_{\rm L}$ is the angular distance to the SN/CB system. In Fig. 57 we show $\Delta(t)$ for SN1998bw/GRB 980425 with our parameters fit to the corresponding radio data (for our adopted H₀, $D_{\rm L}\simeq D_A\simeq 38$ Mpc). In Dar & De Rújula (2000a) we argued that this separation was sufficient to justify a dedicated effort to search for a ``binary'' source. It is interesting to discuss what the situation is with the data currently available.

	Figure 57: The predicted angular separation of SN1998bw and GRB 980425, in milliarcseconds, as a function of time.
Open with DEXTER

The most accurate determination of the position in the sky of the SN1998bw/GRB 980425 system is based on the radio observations made with the Australian Telescope Compact Array (ATCA, Wieringa et al. 1998). Recall that in the CB model the radio coordinates are those of the CB (GRB 980425 was a single-pulse GRB, that is, it had a single dominant CB). In days 3, 4 and 10 the source is reported to be at (RA 19:35:03.31, Dec -52:50:44.7). In the subsequent 33 observations, ranging from day 12 to day 790, the position is (RA 19:35:03.32, Dec -52:50:44.8), some $0\hbox{$.\!\!^{\prime\prime}$ }18$away from the original determination, but not inconsistent with the observational uncertainty of $0\hbox{$.\!\!^{\prime\prime}$ }1$. In the penultimate observation at day 320 the source has faded to the point that it is not observable in 2 out of 6 frequencies, and in the last observation at date 790 there is no clear sighting at any frequency. The predicted values of $\Delta \alpha$from Eq. (30) at some relevant dates are 12, 158, 183 and 292 mas at days 12, 249, 320 and 790, respectively. These results, the observational error, and the fact that the ATCA observers were not trying to follow the source's motion imply that their results are insufficient to claim either that the early change of position was significant, or that a motion of the CB comparable to the predicted one is excluded.

Observations of the vicinity of the source of GRB 980425 were made with the Hubble Space Telescope (HST) at day 778 (Fynbo et al. 2000), with a tiny astrometric uncertainty of $0\hbox{$.\!\!^{\prime\prime}$ }018$, and pointing at ATCA's first reported coordinates. The observations are compatible with SN1998bw lying at that point, and reveal six other objects in a ( $1\hbox{$.\!\!^{\prime\prime}$ }0\times 1\hbox{$.\!\!^{\prime\prime}$ }0$) field centered there. As a result of our CB model fit to the radio data, as we have explained, we expect the optical observations to correspond to SN1998bw, and there it is, at the field's center. We also expect, as in Fig. 55, the CB to be more than two orders of magnitude fainter: not observable. It would be nice if this conclusion was wrong, that is, if the large ``naive'' extrapolation from radio to optical frequencies in Fig. 55 was an underestimate by a considerable factor, which is the case for the larger extrapolation from optical to X-ray frequencies in Fig. 56 (the ``naive'' prediction there is the one labelled p=2.2). In that case, it may be that a subsequent observation of the same field reveals that one of the closer-by extra sources has faded away! Three of these sources are $\sim$ $0\hbox{$.\!\!^{\prime\prime}$ }5$away from the SN, if one of them is the CB, and it is dimming, we would not excessively mind that this is $\sim$60% more distant than the prediction in Fig. 57, based on a constant-density approximation for the ISM.

10 The normalization of afterglows

The values of the CB model parameters that were fitted to the broad band data on GRBs with known redshift - and are listed in Table 3 - are narrowly distributed around their reference values, except for the overall normalization which is much smaller than originally anticipated if $\eta=1$. This normalization ``problem'' may point to inaccuracies in the various hypothesis that we have made. One example is the contention that all of the incident energy of the ISM electrons is radiated in the CB. It may well be that the moving CB deflects and scatters the ISM electrons before they radiate a large fraction of their acquired energy, as suggested by the results of the numerical simulations of Achterberg et al. (2001). But abandoning some of our simplifications would be premature. Indeed, in concluding that in the CB model the normalization of the AGs is more than one order of magnitude too large, we have used our reference parameters to compute the expected values. And there is sufficient elasticity in these parameters to obtain a consistent overall picture of all GRB properties, as we proceed to review and discuss.

11 The parameters of the CB model

With the current analysis of GRB radio AGs we have completed a first round of the study of GRB properties in the CB model, and it behooves us to look back at the various constraints on the relevant parameters.

In Dar & De Rújula (2000a) we followed Dar (1998) and Dar & Plaga (1999) in suggesting that the large peculiar velocities of neutron stars may be due to a ``natal kick'', induced by a momentum imbalance in the oppositely-directed jets of CBs accompanying their birth. On this basis we chose as a reference value $E_{\rm CB}\sim 10^{52}$ erg, for a jet with a reference number of CBs (or prominent peaks in the GRB light-curve) $n_{_{\rm CB}}\sim 10$. Based on a first analysis of AG properties, and of GRB $\gamma$-ray fluences and individual $\gamma$-ray energies, we set $\gamma_0=10^3$as a reference value.

In Dar & De Rújula (2000b) we investigated two extreme models meant to bracket the behaviour of a CB as it crosses a SN shell or its progenitor's ``wind", is heated by the collision with its constituents, and emits observable $\gamma$-rays as it reaches the shell's transparent outskirts with a radius $R_{_{\rm CB}}^{\rm tr}$, proportional to its early transverse expansion velocity $\beta_{\rm trans}\,c$, which we assumed to be close to the sound speed in a relativistic plasma, $\rm\beta_{trans}=1/\sqrt{3}$. In our ``surface'' model, which is no doubt closer to a realistic description, the energy of the GRB in $\gamma$-rays is proportional to $n_{_{\rm CB}}\, [R_{\rm CB}^{\rm tr}]^2 \,\gamma_0$. (Eq. (45) of Dar & De Rújula 2000b). For the chosen reference parameters, in the surface model, this prediction overestimates the GRB fluences by about one order of magnitude. Since the individual $\gamma$-ray energies corroborate the choice $\gamma_0\sim 10^3$, this means that $[R_{_{\rm CB}}^{\rm tr}]^2$ (and $\rm\beta_{trans}$) are overestimated by roughly one order of magnitude.

In Dar & De Rújula (2001) we analyzed the X-ray ``Fe'' lines observed in the AGs of some GRBs, which we attributed to hydrogen recombination in the CBs, with the corresponding Lyman-$\alpha$ lines boosted by a large factor $\delta/(1+z)\sim 500$. We equated the total number of photons in the lines to the baryon number of the jet of CBs, and found agreement with the baryon number in the jet, $n_{_{\rm CB}}\,N_{\rm CB}$, to within one order of magnitude. But in the current investigation, we have found that the absorption of radio waves keeps the CBs hot and ionized (Appendices C and E). This means that our reference value of  $N_{\rm CB}$ is likely to be an overestimate.

In DDD 2001 we proposed a mechanism that would quench the expansion of a CB in minutes of observer's time, well after it has exited the SN shell. The CBs reach an asymptotic radius (Eq. (16) of DDD 2001):

$$R_{\rm max}^3\simeq {3\,N_{\rm CB}\,\beta_{\rm trans}^2\over 2\,\pi\,n_p\,\gamma_0^2}\cdot$$ (32)

On the basis of this calculated radius, for $\rm\beta_{trans}= 1/(3\sqrt{3})$, we found that the normalization of optical and X-ray AGs agreed with the reference-value expectations. On the same basis, we find now that the normalization is overestimated by an order of magnitude. The reason for the discrepancy is that, in DDD 2001, we effectively placed the spectral discontinuity at a ``cooling break'' frequency corresponding to an electron Lorentz factor $\rm\gamma_e\sim 1$, while we have now argued that the discontinuity should occur at a higher value $\gamma_{\rm e}=\gamma(t)$.

Both the GRB fluence and the AG fluence are, in the CB-model, $F\propto n_{_{\rm CB}}\,R^2$, with $R=R_{_{\rm CB}}^{\rm tr}$ for the $\gamma$ rays and $R=R_{\rm max}$ for the AG. At a value of $x_\infty$ fixed by the fit to the AG's temporal behaviour, the AG fluence is:

$$F_{\rm ~AG}\propto n_{_{\rm CB}}\,n_{e}\,R_{\rm max}^2= n_{_{\rm CB}}\,N_{\rm CB}\,{1\over \pi\, x_\infty}\cdot$$ (33)

All of the above ``problems'' are solved if we reduce our ``typical'' values of $R_{\rm max}^2$ and $N_{\rm CB}$by about one order of magnitude, relative to our reference parameters with, according to Eq. (32), the corresponding reduction of the choice of $\rm\beta_{trans}$ by half an order of magnitude.

The precise location of the injection bend is not predictable and a modification by up to one order of magnitude of its position has a small effect on the quality of the fits to observations. An increase of the cooling break frequency $\rm\nu_b$ implies a corresponding decrease in AG flux, see Eq. (4), adding to the uncertainty in the prediction of the precise overall normalization.

To summarize, the CB model correctly describes, in terms of a very limited set of parameters, the properties of GRBs and their AGs, including their normalizations. This is the case even if we adhere to all of the detailed assumptions we have made, even though they are approximations to a no doubt fairly convoluted physical problem.

12 Hyperluminal CBs and radio scintillations

The radio AGs of GRBs often show temporal variations of a factor of two or more on a time scale of hours at early times and on a time scale of days at later times; e.g. GRB 000926 in Figs. 15, 16, GRB 991216 in Fig. 22, GRB 991208 in Figs. 30, 31, GRB 000418 in Fig. 36, GRB 990123 in Fig. 35 and GRB 970508 in Figs. 47, 48.

Similar variations have not been seen in the optical and X-ray bands. The intensity variations of GRB radio AGs are very reminiscent of the ones seen in radio signals from pulsars in our galaxy, interpreted as scintillations due to the motion of the line of sight through the refractive, diffractive and dispersive ISM of the Galaxy (see, e.g., Lyne & Smith 1982). Some very compact active galactic nuclei also show an intraday variability that has been the subject of much debate (e.g., Wagner & Witzel 1995 and references therein). At least in one case - the variations in the radio intensity of the quasar J1819+3845, the most extremely variable AGN known at radio wavelengths (Dennett-Thorpe & de Bruyn 2000) - it was shown unambiguously that the variations are scintillations caused by the ISM (Dennet-Thorpe & Bruyn 2002).

The (de)coherence properties in time and frequency of the radio scintillations have been used to measure the transverse speed of pulsars (e.g., Lyne & Smith 1982). Gupta (1995) has demonstrated for a sample of 59 pulsars that their transverse speed, $V_{\rm iss}$, measured from their inter-stellar scintillations, agrees well with their transverse speed, $V_{\rm pm}$, measured from their proper motion (see also Nicastro et al. 2001).

The movement of the line of sight to pulsars is in most cases dominated by their proper motion at a transverse velocity $V_{\rm pm}$ larger than the turbulent speeds in the ISM, or of the sun relative to the ISM, or of the Earth around the sun. The mean $V_{\rm pm}$ of Gupta's 59 pulsars is 311 $\rm km\, s^{-1}$ and their mean distance is estimated to be 1.96 kpc. Their angular speeds are within an order of magnitude of a central value:

$$\dot \omega_{ps}\sim {\langle V_{\rm pm}\rangle \over \langle D\rangle} \simeq 5.1\times 10^{-15}\, \rm rad\, s^{-1}.$$ (34)

Travelling with a characteristic $\gamma\sim 10^3$ and viewed at typical angles $\theta$ of milliradians, CBs have apparent superluminal velocities, $V_{_{\rm CB}}$ of Eq. (30), that are so high (a few hundred times the speed of light) that they deserve to be called hyperluminal. The angular speed in the sky is:

$$\dot\omega_{_{\rm CB}}(t)= {V_{_{\rm CB}}(t)\over D_A}\simeq {\gamma(t)\, \delta(t)\, c\, \theta\over (1+z)\, D_A}\, \cdot$$ (35)

For the reference values $\theta\sim 1$ mrad and an initial $\gamma_0\sim\delta_0\sim 10^3$, the initial angular speed of a CB at redshift z=1 is $\rm\dot\omega_{_{CB}}(0)\sim 2.7\times 10^{-15}$ rad s^-1, in the very same range as that of Galactic pulsars. The CBs' angular velocity $\dot\omega_{_{\rm CB}}(t)$ and the resulting (inverse) coherence time of the scintillations should decline as $\gamma(t)\,\delta(t)$ does. Both pulsars and CBs are pointlike from the point of view of their radio scintillations. Thus, all conditions are met to expect pulsar-like scintillations in the radio signals from CBs.

The deviations from a smooth behaviour of the radio signals in the case of GRB 980425, as can be seen in Figs. 51, 52, are chromatic, but correlated in time over a much longer period than for the other GRBs. Because GRB 980425 is so close (z=0.0085) and is viewed at the unusually large angle of $\sim$8 mrad (Table 3 and DDD 2001), its apparent angular velocity, Eq. (35), is much larger than for other GRBs. The line of sight to this GRB swept a much bigger region of galactic ISM than for other GRBs or, for that matter, pulsars. Thus, we have no independent information on the ISM irregularities causing scintillations on this large scale.

The analysis of CB scintillations could result in a measurement of their hyperluminal speeds and a decisive test of the cannonball model (fireballs do not have relativistic proper motions, firecones stop moving close to their progenitors and, unlike CBs, have an increasing size that should rapidly quench their scintillations with time). The presently available information (or the current information in its published form) is insufficient for us to attempt at the moment to extract conclusions about CB hyperluminal velocities from the observed scintillation patterns in the radio AG of GRBs.

13 Conclusions

The Cannonball model gives an excellent and extremely simple description of all measured properties of GRB afterglows, including their radio afterglows.

In the CB model, there is an injection bend in the spectrum, at the predicted time-dependent frequency $\rm\nu_b$ of Eq. (14). We have shown that the evidence for the correctness of this prediction is very strong, see Table 2 and Figs. 3 and 4. It is this spectral bend that governs the relative normalization of the radio and the optical AG, again in agreement with observation, as shown in all our figures of AG wide-band spectra.

Since we have always set the electron index to its theoretical value, p=2.2, just three intrinsic parameters are needed to describe an optical or X-ray AG: $\gamma_0$, $x_\infty$ and the normalization; the viewing angle $\theta$, although it must also be fit, is external to the GRB, like the redshift and the absorption in the host and in the Galaxy are. We have shown that, in the CB model, the extension of these results to the radio domain requires the introduction of just one extra parameter: the free-free absorption frequency $\rm\nu_a$ of Eq. (23), and that, in spite of various approximations, this simplest of descriptions is at the moment entirely satisfactory. Notice that what one has to parametrize is a two dimensional surface: the fluence as a function of frequency and time. The shape of this surface is that of a relatively simple ``mountain'', various cuts of which at fixed $\rm t$ or $\nu$are shown if Fig. 1. It would be easy, and it may well be misleading, to overparametrize this rather featureless surface with more than a few parameters.

It is instructive to compare, or so Occam would have thought, the understanding of wide-band AG spectra in the CB model with that in the fireball or firetrumpet models. In the latter, the number of intrinsic parameters varies: seven (e.g. Berger et al. 2001a), eight (e.g. Yost et al. 2001) nine (e.g. Yost et al. 2002) and even thirteen (e.g. Galama et al. 2000). This counting does not include the viewing angle, since the firetrumpets in these works point precisely at the observer. Moreover, even before the ``break'' in the time-evolution - a period during which it is not inconsistent to use the quasi-spherical self-similar approximation of Blandford & McKee (1976) for the expanding material - the ordering of the ``breaks'' in frequency implies a multiple choice of spectral shapes and of their evolution (Granot & Sari 2002).

Countrary to established custom, we are not presenting the $\chi^2$values of our fits, which are generally reasonable and would become quite good if, again following the consuetudinary path, we artificially increased the errors to compensate for scintillations in the radio data and/or uncertainties in attenuation. The reason is that the CB model is a very simplified description of a no doubt very complicated reality (e.g. CBs could be somewhat comet-like, as opposed to spherical, their inner distributions of density, ionization, magnetic field and temperature could be non-trivial, even chaotic, etc.). Even when the physics is much simpler than in the analysis of radio emissions, and the fits are very good - as is the case in our description of optical and X-ray AGs in DDD 2001 - we do not report their quite impressive $\chi^2$values. We view our ``fits'' as rough descriptions, rather than true fits. Under such circumstances, the overintrepretation of a $\chi^2$ test has every chance of being misleading, much more so in models containing many more parameters than the CB model.

For the same reasons, and because of the systematic errors in the data, the values of the parameters we extract from our fits should not be taken entirely at face value, even though the minimization procedure - which attributes to the errors a counterfactual purely statistical origin - results in tiny 1 $\sigma$ spreads for the fitted parameters, and in $\chi^2$ values that are in most cases satisfactory.

In the radio domain, as in every other aspect, the pair SN1998bw/GRB 980425 is particularly fascinating. On the basis of this GRB's observed fluence and distance, and given the (totally trivial but all important) dependence of the fluence on observation angle, we claimed in Dar & De Rújula (2000a) that the only peculiarity of this pair was that it was observed uncharacteristically far from its axis (for a GRB) and uncharacteristically close to it (for a SN). In DDD 2001 we proved that the X-ray AG of GRB 980245 was also what is expected in the CB model, depriving the supernova of its X-ray peculiarity: it did not make the observed X-rays. In this paper, by understanding the magnitude, time- and frequency-dependence of the pair's radio signals - which were not emitted, either, by the SN - we have demonstrated that SN1998bw was also ``radio normal''. Neither this GRB, nor its SN have - in the CB model - anything in particular, except the chance occurrences of the distance and observation angle. Alas, the unique occasion to make a fundamental discovery by actually resolving the SN and the CB, as proposed in Dar & De Rújula (2000a), may now be very difficult, but, as we have explained, not entirely out of the question.

By pure coincidence, the apparent angular velocities of galactic pulsars and cosmological cannonballs are of the same order of magnitude. The analysis of radio scintillations, one of the methods used to measure pulsars velocities, should also be applicable to the GRB ejecta. Thus, it ought to be possible to test the CB-model's prediction of hyperluminal cannonball velocities.

Appendix A: The slowdown of a CB

We review the functional form of the time dependent Lorentz factor $\gamma(t)$, which is explicit and analytical in a fair approximation (DDD 2001).

In minutes of observer's time, CBs reach a roughly constant radius $R_{\rm max}$ and are parsecs away from their progenitor star, a domain where a constant-density ISM may be a reasonable approximation. Relativistic energy-momentum conservation in the progenitor's rest frame results in the equation governing the deceleration of a CB in the ISM:

$$M_{_{\rm CB}}\, {\rm d}\gamma =-\, m_p\,c^2\, n_p\, \pi\, R_{\rm max}^2\, \gamma^2\, c\, {\rm d}t_{\rm SN} .$$ (36)

Interestingly, the above expression is correct both if the incoming ISM protons are isotropically reemitted in the CB rest frame, or if they are ingurgitated by the CB (in the first case, they are reemitted with average energy $m_{p}\,c^2\,\gamma^2$ in the progenitor's frame, in the second, the change in $\gamma$ per added proton is ${\rm d}\gamma=-[m_{p}/M_{_{\rm CB}}]\gamma$).

Use the relation ${\rm d}t_{\rm SN}=\gamma(t)\, {\rm d}t$ between the times measured in the supernova and CB rest frames, divide both sides of the Eq. (36) by $M_{_{\rm CB}}\, \gamma^3$ and integrate to obtain the relation:

$${1\over \gamma^2(t)} - {1\over \gamma_0^2}\simeq {2\, c\, t\over x_\infty} ,$$ (37)

where t is CB time, and:

$$x_\infty\equiv{N_{\rm CB}\over\pi\, R_{\rm max}^2\, n_{p}},$$ (38)

with $N_{\rm CB}\approx M_{_{\rm CB}}/m_{p}$ the CB's baryon number.

It is important to know the number of electrons accumulated by a CB as its Lorentz factor decreases from $\gamma_0$ to $\gamma(t)$ (in the approximation n_e=n_p of a Hydrogenic ISM this number equals that of scattered or incorporated protons). The number rate of accumulation is related to the energy-loss rate of Eq. (36) so that:

$${\rm d}N= - \eta\, {M_{_{\rm CB}}\, {\rm d}\gamma\over m_{p}\... ...^2}= -\eta\, N_{_{\rm CB}}\,{{\rm d}\gamma\over \gamma^2}\cdot$$ (39)

Assuming constant $\eta$, the total number of ISM electrons accumulated at a CB time t is then:

$$N(t)=\eta\, N_{_{\rm CB}}\,\left[{1\over \gamma(t)}-{1\over \gamma_0}\right]\cdot$$ (40)

The time-dependence of $\gamma(t)$ with t the observer's time is more complicated than Eq. (37): the relation between the two times ( ${\rm d}t_{\rm obs}={\rm d}t_{_{\rm CB}}(1+z)/\delta$) introduces a $\gamma$ (or t) dependence via $\delta$. The result for $\gamma(t_{\rm obs})$is (DDD 2001):

 

$$\gamma \gamma(\gamma_0,\theta,x_\infty;t) = {1\over B} \,\left[\theta^2+C\,\theta^4+{1\over C}\right]$$ =

$$\equiv \left[{2\over B^2+2\,\theta^6+B\,\sqrt{B^2+4\,\theta^6}}\right]^{1/3}$$ C

$$\equiv {1\over \gamma_0^3}+{3\,\theta^2\over\gamma_0}+ {6\,c\, t\over (1+z)\, x_\infty}\cdot$$ B (41)

The Lorentz factor of the CB decreases from $\gamma_0$ to $\gamma_0/2$ as the CB travels a distance $x_\infty/\gamma_0$, whose reference value is 1.3 kpc, as in Table 1.

Appendix B: The synchrotron cooling break

We argue that the conventional synchrotron spectral break occurs at a very non-relativistic electron energy. The corresponding break in the radio spectrum is unobservable.

In writing the electron energy-loss rate Eq. (10), we have assumed that synchrotron radiation, which is quadratic in energy, dominates (inverse Compton scattering has the same energy dependence, but it is negligible, since the magnetic energy density within a CB is much higher than the radiation energy density). The general result for the energy loss of high-energy electrons is of the form:

$$-{{\rm d}E\over {\rm d}t}\simeq A_{\rm C}\,({\rm ln} {E\over m_{e}\,c^2}+a)+A_{\rm B}\,E+A_{\rm S}\, E^2.$$ (42)

The term proportional to $A_{\rm C}$ describes Coulomb scattering and ionization losses in the CB, which are negligible at high energies. The second term represents bremsstrahlung and its coefficient is (e.g. Shu 1991)

$$A_{\rm B}={34.35\,\alpha\, \sigma_{\rm T}\, c\,\bar{n}_{\rm b} \over 2\, \pi} ,$$ (43)

where $\alpha=1/137$ and $\rm\bar n_b$ is the baryon number density in the CB. Adiabatic losses and electron escape would have the same energy dependence as bremsstrahlung, but in the AG regime we are discussing the CBs are no longer expanding and the electron's Larmor radii are so small - relative to the CB's radius - that escape losses should also be negligible.

The spectral index of high energy electrons injected with a power-law spectrum steepens by one unit at a ``cooling break'' energy $[\beta(E_{\rm c})]^2\,E_{\rm c}=A_{\rm B}/A_{\rm S}$. For $\gamma \simeq 10^3$ and the reference values of $\bar n_{\rm b}=\bar n_{e}$ and n_e, the synchrotron cooling break is at a subrelativistic energy ( $\beta\sim 0.8$). This is in contrast with the injection bend at the highly relativistic energy $E_{\rm b}\simeq \gamma\, m_{e}\, c^2\,.$The synchrotron radiation of electrons below the cooling break is, for the current data, at unobservably low observer's radio frequencies.

Appendix C: Photoionization and recombination in the CB

We argue that the synchrotron radiation in a CB is intense enough to maintain its plasma partially ionized with ion and free electron densities proportional to $\gamma(t)$.

The bound-free cross section for photoionization of atomic hydrogen in its nth excited state by photons with frequency above the ionization threshold, $\nu_n=3.29\times 10^{15}/n^2\, \rm Hz$, is given by $\sigma_\nu(n)=n\,\sigma_1\,\bar{g}_n (\nu/\nu_n)^{-3}$, with $\sigma_1= {64\, \alpha\, \pi\, a_0^2/(3\, \sqrt{3}}) \simeq 7.91\times 10^{-18}$ cm² ( $a_0=0.53\times 10^{-8}$ cm is the Bohr radius and $\bar{g}_n$ is the Gaunt factor for photoabsorption by hydrogen). For the surface flux of photons of Eq. (6), we obtain an ionization rate of the nth level of atomic hydrogen:

$$R_{\rm i}(n)= {\eta\, n_{e}\, m_{e}\, c^3 \gamma(t)^2\, n\, \... ...\, \nu_n}\, \left({\nu_{\rm b}\over\nu_n}\right)^{(p-2)/ 2}.$$ (44)

For the reference values of n_e, p and $\gamma=\gamma_0$, the ionization rate of the ground state is $R_{\rm i}(1)\sim 1.1\times 10^{-2}\,\eta\,\rm s^{-1}$.

The recombination rate per unit volume of hydrogen in an hydrogenic CB is (Osterbrock 1989):

$$R_{\rm rec}\simeq 1.0\times 10^{-12}\,\bar n_{e}\, \left[{T\over 10^4\,{\rm K}}\right]^{-0.7}\,{\rm s}^{-1} .$$ (45)

For the reference value of the CB parameters, and $T\,=\,10\,000$ K the recombination rate of hydrogen is $R_{\rm rec}\sim 1.1\times 10^{-5}\, \rm s^{-1}$. In quasi equilibrium, the ionization rate per unit volume, which is proportional to the number density of recombined hydrogen atoms, must be equal to the recombination rate per unit volume, which is proportional to the product of the ion and free electron densities in the CB. Thus, initially the CB is highly ionized. But, for small values of $\eta$ and later times when $\gamma(t)$ becomes sufficiently small, equilibrium between the ionization and recombination rates in the partially ionized hydrogenic plasma results in $\bar n_{i}=\bar n_{e}\propto \gamma(t)\, .$

Appendix D: Synchrotron and Bremsstrahlung self absorption

We argue that the self-attenuation in the CB of the observed radio waves is dominated by free-free absorption.

The density of energetic electrons

In the rest system of a CB, the ISM electrons arrive at a rate ${\rm d}\,N_{\rm e}/{\rm d}t\simeq n_p\,\gamma\, \pi\, R_{\rm max}^2\, c.$A fraction $\eta$ of their energy, $E_{\rm b}=m_{e}\, c^2\, \gamma,$ is synchrotron re-radiated. Let $n_{\rm eff}$ be the density of the emitting electrons, so that:

$$\eta\, E_{\rm b}\, {{\rm d}N_{\rm e}\over {\rm d}t}=\int F_{_... ...{\rm eff}\over {\rm d}E_{\rm e}}\,{1\over \tau(E_{\rm e})}\; ,$$ (46)

with $\tau(E_{\rm e})=E_{\rm e}/({\rm d}E_{\rm e}/{\rm d}t)$ the cooling time for electrons of energy E_e, determined from Eqs. (2) and (10) to be:

$$\tau(E_{\rm e})=4\,{m_{e}\over m_{p}}\,{1\over n_{p}\,\sigma_{_{\rm T}}\,c\,\gamma_{\rm e}^3} \cdot$$ (47)

For the electron spectrum of Eq. (13), the second integral in Eq. (46) is dominated by energies $E_{\rm e}\sim E_{\rm b}$( $\rm\gamma_e\sim \gamma_b=\gamma$). Thus, for a uniform distribution of electrons in the CB's volume V, we obtain:

 

$$n_{\rm eff} \simeq -\,{\eta\over V}\,{{\rm d}N_{\rm e}\over {\rm d}t}\,\tau(E_{\rm b})$$

$${m_{e}\over m_{p}}\,{3\,\eta\over R_{\rm max}\,\sigma_{_T}\,\gamma^2} \simeq (11\,\eta\, {\rm cm}^{-3})\left[10^3\over\gamma\right]^2 ,$$ = (48)

where we have used our reference $R_{\rm max}$. This density could be somewhat higher if the emitting electrons are concentrated on the CB's front surface. Note that this density increases with time like $[\gamma(t)]^{-2}$.

Synchrotron self absorption

For a power-law distribution, ${\rm d}n_{e}/{\rm d}\gamma_{\rm e}= (p-1)\,n_{\rm eff}\, \gamma_{\rm e}^{-p}$, the correct attenuation coefficient for synchrotron self absorption at frequency $\nu$ is (e.g., Shu 1991, Eqs. (19.37), (38)):

$$\chi_\nu= K_0\, (p-1)\,n_{\rm eff}\, {B_\perp}^{(p+2)/2}\, \nu^{-(p+4)/2}\, ,$$ (49)

where:

$$K_0={c\, r_{\rm e}\over 4\, \sqrt{3}}\, \left ({3\, e\over 2... ...{3\, p+2\over 12}\right) \Gamma\left({3p+22\over 12}\right),$$ (50)

with $r_{\rm e}= {\rm e}^2/m_{e}\, c^2.$ An observed frequency $\rm\nu_{obs}$ was emitted at $\nu(t)=(1+z)\, \nu_{ob}/\delta(t)$ in the CB's rest frame. As an example, $\nu_{\rm ob}=5$ GHz from a decelerating CB with $\delta(t)\simeq \gamma_0/2 \simeq 500$, if emitted at a typical z=1, corresponds to $\nu=20$ MHz in the CB rest frame. For our reference parameters, the synchrotron self absorption coefficient in the CB is $\chi_\nu \simeq 2.4\times 10^{-10}\,\eta\, \rm cm^{-1}$. Since $n_{\rm eff}\propto \gamma^{-2}$, $B\propto \gamma$, and, after a few observer's days, $\delta\sim 2\gamma$ and $\gamma(t)\sim t^{-1/3}$, $\chi_\nu$ decreases with time like $\gamma^{(p+1)}\sim t^{-(p+1)/3}\sim t^{-1.1}$.

Bremsstrahlung self absorption

The X-ray AG is dominated first by bremsstrahlung from plasma electrons and later by synchrotron radiation from the swept up high energy electrons (DDD 2001). The observed X-ray flux, or the theoretical UV flux in the CB rest frame, can be used to show that the CB is partially ionized during the radio AG observations and that the ionized fraction of the CB plasma is proportional to $\gamma(t)$ (see Appendix C). The logarithmic dependence of the plasma temperature in the Saha equation on the fractional ionization, keeps the CB's temperature nearly constant during its  AG phase. Consequently, in the CB rest frame, the free-free attenuation at a fixed frequency is proportional to $[\gamma(t)]^2$ and the free-free (bremsstrahlung) absorption coefficient is that of Eq. (20).

The temperature of the partially ionized CB is of ${\cal{O}}(1)$ eV and almost constant during the observed AG. For $\sim$20 MHz emission from a thermal plasma at such temperature, $g\sim 10$and for one tenth of the typical bulk CB density, $\bar n_{e}\sim 10^6~ \rm cm^{-3}$, one obtains from Eq. (20) $\chi_\nu\simeq 4\times 10^{-10}\,\rm cm^{-1}$, which is $\sim$$1.7/\eta$ larger than the synchrotron absorption coefficient of the energetic electrons in the CB (the values of $\eta$ are listed in Table 3). At a fixed observer frequency, $\nu =(1+z)\,\nu_{\rm ob}/\delta$, the free-free opacity of the CB decreases roughly like $\sim$ $\gamma^2\sim t^{-2/3}$ compared with the $\sim$t^-1.1 decline of the synchrotron self opacity.

The conclusion is that free-free absorption is dominant for as long as the ionization of the CB is considerable.

Appendix E: Emission of self absorbed radiations

We argue that the energy of the self absorbed radio waves and ionizing photons in the CB is radiated mainly by thermal bremsstrahlung and line emission from the CB contributing significantly to the observed X-ray afterglow. The absorbed radio power is roughly equal to the integrated emissivity of the CB over all frequencies below $\rm\nu_a$, defined by Eq. (23). For the spectrum of Eq. (4), and the normalization of Eq. (5), the absorbed power is:

$${{\rm d}E_{\rm ab}\over {\rm d}t}\simeq {\eta\, \pi\, R_{\rm ... ...1)}\, \left[{\nu_{\rm a}\over \nu_{\rm b}}\right]^{1/2}\cdot$$ (51)

The CB self absorbed radio energy becomes part of the thermal energy of the CB plasma. It is radiated by the plasma as thermal bremsstrahlung at optical wavelengths (in the CB rest frame). For our reference parameters, $\rm\nu_a\sim$ 100 MHz and $\eta<1$, this absorbed power is smaller than the power absorbed by photoionization.

The recombination energy is radiated at a rate $\approx$ $R_{\rm rec}\, x\, N_{\rm cb} \, I$ in the CB rest frame where $x=\bar n_{e}/\bar n_{\rm b}$ is the fraction of ionized hydrogen in the CB and $I=13.6\,\rm eV$ is the binding energy of hydrogen in its ground state. In the distant observer frame, the observed radiation is boosted and collimated by the highly relativistic motion of the CB and redshifted by the cosmological expansion to:

$${{\rm d}E_{\rm rec}\over {\rm d}t} \simeq {R_{\rm rec}\, x\,... ...\, I\, (1+z)\, [\delta(t)]^4\over 4\, \pi\, D_{\rm L}^2}\cdot$$ (52)

For our reference parameters, hydrogen recombination produces X-ray lines with a total energy flux of $\sim$ $x^2\, \times 10^{-12}\,\rm erg\, s^{-1}\,cm^{-2}\, .$

Due to their large Doppler shift $\delta$, the hydrogen emission lines (and the emission lines from the swept up ISM and supernova shell material) as well as the CB's thermal bremsstrahlung, are shifted to the observer's X-ray band. They contribute significantly to the X-ray afterglow and may provide a simple alternative explanation (Dar & De Rújula 2000) to the commonly assumed Fe-line origin of the X-ray lines observed in the afterglows of GRB 970508: Piro et al. (1998), GRB 970828: Yoshida et al. (1999; 2001), GRB 991216: Piro et al. (2000) and GRB 000214: Antonelli et al. (2000).

References

 

• Achterberg, A., Gallant, Y. A., Kirk, J. G., & Guthmann, A. W. 2001, MNRAS, 328, 393 In the text NASA ADS  
• Andersen, M. I., Hjorth, J., Pedersen, H., et al. 2000, A&A, 364, L54 NASA ADS  
• Antonelli, L. A., Piro, L., Vietri, M., et al. 2000, ApJ, 545, L39 In the text NASA ADS  
• Axford, W. I., Leer, E., & Skadron, G. 1997, Proc. International Cosmic Ray Conf., 11, 132  
• Ballard, K. R., & Heavens, A. F. 1992, MNRAS, 259, 89 In the text NASA ADS  
• Bell, A. R. 1978, MNRAS, 182, 147 In the text NASA ADS  
• Berger, E., Sari, R., & Frail, D. A. 2000, ApJ, 545, 56 In the text NASA ADS  
• Berger, E., Diercks, A., Frail, D. A., et al. 2001a, ApJ, 556, 556 In the text NASA ADS  
• Berger, E., Price, P. A., Harrison, et al. 2001b, ApJ, 549, L7 NASA ADS  
• Berger, E., Sari, R., Frail, D., & Kulkarni, S. 2001c, Gamma-Ray Bursts in the Afterglow Era, Rome Workshop, ed. E. Costa, F. Frontera & J. Hjorth (Berlin: Springer-Verlag)  
• Beuermann, K., Hessman, F. V., Reinsch, K., et al. 1999, A&A, 352, L26 In the text NASA ADS  
• Blandford, R. D., & McKee, C. F. 1976, Phys. Fluids, 19, 1130 NASA ADS  
• Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 In the text NASA ADS  
• Castro-Tirado, A. J., Gorosabel, J., Benitez, N., et al. 1998, Science, 279, 1011 NASA ADS  
• Castro-Tirado, A. J., Zapatero-Osorio, M. R., Caon, N., et al. 1999, Science, 283, 2069 In the text NASA ADS  
• Castro-Tirado, A. J., Sokolov, V. V., & Gorosabel, J. 2001, A&A, 370, 398 In the text NASA ADS  
• Chary, R., Neugebauer, G., & Morris, M. 1998, ApJ, 498, L9 In the text NASA ADS  
• Dado, S., Dar, A., & De Rújula, A. 2002, A&A, 388, 1079 In the text NASA ADS  
• Dado, S., Dar, A., & De Rújula, A. 2002 [astro-ph/0207015]  
• Dar, A., & De Rújula, A. 2000a [astro-ph/0008474] In the text  
• Dar, A., & De Rújula, A. 2000b [astro-ph/0012227]  
• Dar, A., & De Rújula, A. 2001 [astro-ph/0102115] In the text  
• Dennett-Thorpe, J., & de Bruyn, A. G. 2000, ApJ, 529, L65 In the text NASA ADS  
• Dennett-Thorpe, J., & de Bruyn, A. G. 2002 [astro-ph/0201061]  
• Di Paola, A., Speziali, R., Antonelli, L. A., et al. 2000, GCN Circ., 816 In the text  
• Frail, D. A., Waxman, E., Kulkarni, S. R., et al. 2000a, ApJ, 537, 191 In the text NASA ADS  
• Frail, D. A., Berger, E., Galama, T., et al. 2000b, ApJ, 538, L129 NASA ADS  
• Fruchter, A. S., Thorsett, S. E., Metzger, M. R., et al. 1999, ApJ, 519, L13 In the text NASA ADS  
• Fynbo, J. U., Holland, S., Andersen, M. I., et al. 2000, ApJ, 542, L89 In the text NASA ADS  
• Fynbo, J. U., Gorosabel, J., Dall, T. H., et al. 2001, A&A, 373, 796 In the text NASA ADS  
• Galama, T. J. Wijers, R. A. M. J., Bremer, M., et al. 1998a, ApJ, 500, L97 In the text NASA ADS  
• Galama, T. J., Groot, P. J., van Paradijs, J., et al. 1998b, ApJ, 497, L13G NASA ADS  
• Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998c, Nature, 395, 670 NASA ADS  
• Galama, T. J., Briggs, M. S., Wijers, R. A. M., et al. 1999, Nature, 398, 394 In the text NASA ADS  
• Galama, T. J., Bremer, M., Bertoldi, F., et al. 2000, ApJ, 541, L45 In the text NASA ADS  
• Garcia, M. R., Callanan, P. J., Moraru, D., et al. 1998, ApJ, 500, L105 In the text NASA ADS  
• Garnavich, P. M., Jha, S., Pahre, M. A., et al. 2000a, ApJ, 543, 61 In the text NASA ADS  
• Garnavich, P. M., Loeb, A., Stanek, K. Z., et al. 2000b, ApJ, 544, L11 NASA ADS  
• Granot, J.,Panaitescu, A., Kumar, P., & Woosley, S. E. 2002, ApJ, 570, L61 NASA ADS  
• Granot, J., & Sari, R. 2002, ApJ, 568, 820 In the text NASA ADS  
• Gupta, Y. 1995, ApJ, 451, 717 In the text NASA ADS  
• Halpern, J. P., Uglesich, R., Mirabal, N., et al. 2000, ApJ, 543, 697 In the text NASA ADS  
• Harrison, F. A., Bloom, J. S., Frail, D. A., et al. 1999, ApJ, 523, L121 In the text NASA ADS  
• Harrison, F. A., Yost, S. A., Sari, R., et al. 2001, ApJ, 559, 123 In the text NASA ADS  
• Holland, S., Björnsson, G., Hjorth, J., & Thomsen, B. 2000, A&A, 364, 467 In the text NASA ADS  
• Iwamoto, K., Mazzali, P. A., Nomoto, K., et al. 1998, Nature, 395, 672 In the text NASA ADS  
• Jensen, B. L., Fynbo, J. U., Gorosabel, J., et al. 2001, A&A, 370, 909 In the text NASA ADS  
• Kay, L. E., Halpern, J. P., Leighly, K. M., et al. 1998, IAU Circ., 6969  
• Klose, S., Stecklum, B., Masetti, N., et al. 2000, ApJ, 545, 271 In the text NASA ADS  
• Kouveliotou, C. 2002, Talk at the GRB 2002 Conf., Rome In the text  
• Krymsky, G. F. 1977, Dok. Acad. Nauk. USSR, 234, 1306 In the text  
• Kulkarni, S. R., Frail, D. A., Wieringa, M. H., et al. 1998, Nature, 395, 663 In the text NASA ADS  
• Kulkarni, S. R., Djorgovski, S. G., Odewahn, S. C., et al. 1999a, Nature, 398, 389 In the text NASA ADS  
• Kulkarni, S. R., Frail, D. A., Sari, R., et al. 1999b, ApJ, 522, L97 NASA ADS  
• Li, Z., & Chevalier, R. A. 1999, ApJ, 526, L716  
• Lidman, C., Doublier, V., Gonzalez, J. F., et al. 1998, IAU Circ., 6895 In the text  
• Lyne, A. G., & Smith, F. G. 1982, Nature, 289, 825 In the text  
• Masetti, N., Bartolini, C., Bernabei, S., et al. 2000, A&A, 359, 23 In the text  
• Masetti, N., Palazzi, E., Pian, E., et al. 2001, A&A, 374, 382 NASA ADS  
• Metzger, M. R., Djorgovski, S. G., Kulkarni, S. R., et al. 1997, Nature, 387, 878 In the text NASA ADS  
• Mirabel, I. F., & Rodriguez, L. F. 1994, Nature, 371, 46 In the text NASA ADS  
• Mirabel, I. F., & Rodriguez, L. F. 1999, ARA&A, 37, 409 In the text NASA ADS  
• Nicastro, L., Nigro, F., D'Amico, N., Lumiella, V., & Johnston, S. 2001, A&A, 368, 1055 In the text NASA ADS  
• Paczynski, B. 1998, ApJ, 494, L45 In the text NASA ADS  
• Panaitescu, A., & Kumar, P. 2002, ApJ, 571, 779 NASA ADS  
• Patat, F., & Piemonte, A. 1998, IAU Circ., 6918  
• Patat, F., Cappellaro, E., Rizzi, L., & Turatto, M. 1998, IAU Circ., 7215  
• Pedersen, H., Jaunsen, A. O., Grav, T., et al. 1998, ApJ, 496, 311 In the text NASA ADS  
• Pian, E., Fruchter, A. S., Bergeron, L. E., et al. 1998, ApJ, 492, L103 In the text NASA ADS  
• Pian, E., Amati, L., Antonelli, L. A., et al. 2000, ApJ, 536, 778 In the text NASA ADS  
• Pian, E. 2002, Talk at the meeting: Gamma Ray Bursts in the Afterglow Era, Third Workshop, Rome, Sep. 2002 In the text  
• Piro, L., Amati, L., Antonelli, L. A., et al. 1998, A&A, 331, L41 In the text NASA ADS  
• Piro, L., Garmire, G., Garcia, M., et al. 2000, Science, 290, 955 In the text NASA ADS  
• Price, P., Harrison, F. A., Galama, T. J., et al. 2001, ApJ, 549, L7 In the text NASA ADS  
• Readhead, A. C. S. 1994, ApJ, 426, 51 In the text NASA ADS  
• Rhoads, J. E., & Fruchter, A. S. 2001, ApJ, 546, 117 In the text NASA ADS  
• Rossi, E., Lazzati, D., & Rees, M. J. 2002, MNRAS, 332, 945 NASA ADS  
• Rybicki, G. B., & Lightman A. P. 1979, Radiative Processes in Astrophysics (John Wiley & Sons, Inc.) In the text  
• Sadler, E. M., Stathakis, R. A., Boyle, B. J., & Ekers, R. D. 1998, IAUC Circ., 6901 In the text  
• Sagar, R., Mohan, V., Pandey, A. K., Pandey, S. B., & Castro-Tirado, A. J. 2000a, BASI, 28, 15 In the text NASA ADS  
• Sagar, R., Mohan, V., Pandey, S. B., et al. 2000b, BASI, 28, 499 NASA ADS  
• Sagar, R., Pandey, S. B., Mohan, V., Bhattacharya, D., & Castro-Tirado, A. J. 2001, BASI, 29, 1 In the text NASA ADS  
• Sahu, K. C., Livio, M., Petro, L., et al. 1997, ApJ, 489, L127 NASA ADS  
• Sahu, K. C., Vreeswijk, P., Bakos, G., Menzies, J. W., et al. 2000, ApJ, 540, 74 NASA ADS  
• Salmonson, J. D., & Galama, T. J. 2002, ApJ, 569, 682 NASA ADS  
• Schaefer, B., Schaefer, M., Smith, P., et al. 1997, IAU Circ., 6658 In the text  
• Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 In the text NASA ADS  
• Shu, F. H. 1991, in The Physics of Astrophysics, University Science Books In the text  
• Smette, A. 2001, ApJ, 556, 70 In the text NASA ADS  
• Soffita, P., Feroci, M., Piro, L., et al. 1998, IAU Circ., 6884 In the text  
• Sokolov, V. V., Kopylov, A. I., Zharikov, S. V., et al. 1998, A&A, 334, 117 In the text NASA ADS  
• Sollerman, J., Kozma, C., Fransson, C., et al. 2000, ApJ, 537, L127 In the text NASA ADS  
• Stanek, K. Z., Garnavich, P. M., Kaluzny, J., Pych, W., & Thompson, I. 1999, ApJ, 522, L39 In the text NASA ADS  
• Stanek, K. Z., Garnavich, P. M., Jha, S., et al. 2001, ApJ 563, 592 NASA ADS  
• Tinney, C., Stathakis, R., Cannon, R., et al. 1998 IAU Circ., 6896 In the text  
• Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 In the text NASA ADS  
• Weiler, K. W., Panagia, N., & Montes, M. 2001, ApJ, 562, 670 NASA ADS  
• Wieringa, M., Frail, D. A., Kulkarni, S. R., Higdon, J. L., & Wark, R. 1998, GCN Circ., 63 In the text  
• Yoshida, A., Namiki, M., Gtani, C., et al. 1999, A&AS, 138, 433 In the text NASA ADS  
• Yoshida, A., Namiki, M., Yonetoku, D., et al. 2001, ApJ, 557, L27 In the text NASA ADS  
• Yost, S. A., Sari, R., Harrison, F. A. et al. 2001, Gamma-Ray Bursts in the Afterglow Era, Rome Workshop, ed. E. Costa, F. Frontera & J. Hjorth (Berlin: Springer-Verlag) In the text  
• Yost, S. A., Frail, D. A., Harrison, F. A., et al. 2002, ApJ, 577, 155 In the text NASA ADS  
• Zhang, B., & Meszaros, P. L. [astro-ph/0112118]  
• Zharikov, S. V., Sokolov, V. V., & Baryshev, Yu. V. 1998, A&A, 337, 356 In the text NASA ADS

 

Online Material

Figure 6: Comparisons between our fitted CB model AG of GRB 000301c, at z=2.033, Eq. (8) and Fig. 5, with the observed optical data. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contributions of the underlying galaxy and an expected (but, in this case, unobservable) SN1998bw-like SN have been subtracted.

Open with DEXTER

	Figure 7: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000301c. Upper panel: the light curve at 350 GHz. Lower panel: the light curve at 250 GHz.
Open with DEXTER

	Figure 8: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000301c. Upper panel: the light curve at 100 GHz. Lower panel: the light curve at 22.5 GHz.
Open with DEXTER

	Figure 9: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000301c. Upper panel: the light curve at 15 GHz. Lower panel: the light curve at 8.46 GHz.
Open with DEXTER

	Figure 10: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000301c. Upper panel: the light curve at 4.86 GHz. Lower panel: the light curve at 1.43 GHz.
Open with DEXTER

	Figure 11: The spectrum of the AG of GRB 000301c from radio to optical frequencies. Upper panel: in the time interval between 1 and 5 days after burst. Lower panel: in the time interval between 5 and 10 days after burst. The highest peaking curve in the upper pannel corresponds to the later time and in the lower panel to the earlier time.
Open with DEXTER

	Figure 12: The spectrum of the AG of GRB 000301c from radio to optical frequencies. Upper panel: in the time interval between 10 and 20 days after burst. Lower panel: in the time interval between 20 and 30 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 13: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed optical afterglow of GRB 000926 at z=2.037. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contributions of the underlying galaxy and an expected (but, in this case, unobservable) SN1998bw-like SN have been subtracted.

Open with DEXTER

	Figure 14: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000926. Upper panel: the light curve at 98.48 GHz. Lower panel: the light curve at 22.5 GHz.
Open with DEXTER

	Figure 15: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000926. Upper panel: the light curve at 15 GHz. Lower panel: the light curve at 8.46 GHz.
Open with DEXTER

	Figure 16: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000926. Upper panel: the light curve at 4.86 GHz. Lower panel: the light curve at 1.43 GHz.
Open with DEXTER

	Figure 17: The spectrum of the AG of GRB 000926 from radio to optical frequencies. Upper panel: in the time interval between 0.8 and 1.4 days after burst. Lower panel: in the time interval between 1.4 and 2.5 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 18: The spectrum of the AG of GRB 000926 from radio to optical frequencies. Upper panel: in the time interval between 2.5 and 4 days after burst. Lower panel: in the time interval between 4 and 8 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 19: The spectrum of the AG of GRB 000926 from radio to optical frequencies. Upper panel: in the time interval between 8 and 20 days after burst. Lower panel: in the time interval between 20 and 100 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 20: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed optical afterglow of GRB 991216 at z=1.02. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contributions of the underlying galaxy and the expected SN1998bw-like SN have been subtracted. In a CB-model fit, there is in this case some evidence for such a SN (DDD 2001).

Open with DEXTER

	Figure 21: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991216. Upper panel: the light curve at 350 GHz. Lower panel: the light curve at 100 GHz.
Open with DEXTER

	Figure 22: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991216. Upper panel: the light curve at 15 GHz. Lower panel: the light curve at 8.46 GHz.
Open with DEXTER

	Figure 23: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991216. Upper panel: the light curve at 4.86 GHz. Lower panel: the light curve at 1.43 GHz.
Open with DEXTER

	Figure 24: The spectrum of the AG of GRB 991216 from radio to optical frequencies. Upper panel: in the time interval between 0.44 and 2 days after burst. Lower panel: in the time interval between 2 and 4 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 25: The spectrum of the AG of GRB 991216 from radio to optical frequencies. Upper panel: in the time interval between 4 and 7 days after burst. Lower panel: in the time interval between 7 and 13 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 26: The spectrum of the AG of GRB 991216 from radio to optical frequencies. Upper panel: in the time interval between 13 and 30 days after burst. Lower panel: in the time interval between 30 and 80 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 27: Comparisons between our fitted CB model AG of GRB 991208, at z=0.706, Eq. (8), with the observed optical data. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contribution of the underlying galaxy and associated supernova has been subtracted. The contributions of the underlying galaxy and the expected SN1998bw-like SN have been subtracted. In a CB-model fit, there is in this case strong evidence for such a SN (DDD 2001).

Open with DEXTER

	Figure 28: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991208. Upper panel: the light curve at 100 GHz. Lower panel: the light curve at 86.2 GHz.
Open with DEXTER

	Figure 29: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991208. Upper panel: the light curve at 30 GHz. Lower panel: the light curve at 22.5 GHz.
Open with DEXTER

	Figure 30: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991208. Upper panel: the light curve at 15 GHz. Lower panel: the light curve at 8.46 GHz.
Open with DEXTER

	Figure 31: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 991208. Upper panel: the light curve at 4.86 GHz. Lower panel: the light curve at 1.43 GHz.
Open with DEXTER

	Figure 32: The spectrum of the AG of GRB 991208 from radio to optical frequencies. Upper panel: in the time interval between 2 and 5 days after burst. Lower panel: in the time interval between 5 and 10 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 33: The spectrum of the AG of GRB 991208 from radio to optical frequencies in the time interval between 10 and 14.3 days. The highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 34: Comparisons between our fitted CB model AG of GRB 000418, at z=1.118, Eq. (8), with the observed optical data. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contributions of the underlying galaxy and the expected SN1998bw-like SN have been subtracted. In a CB-model fit, there is in this case strong evidence for such a SN (DDD 2001).

Open with DEXTER

	Figure 35: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000418. Upper panel: the light curve at 22.46 GHz. Lower panel: the light curve at 15 GHz.
Open with DEXTER

	Figure 36: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 000418. Upper panel: the light curve at 8.46 GHz. Lower panel: the light curve at 4.86 GHz.
Open with DEXTER

	Figure 37: The spectrum of the AG of GRB 000418 from radio to optical frequencies. Upper panel: in the time interval between 9.5 and 30 days after burst. Lower panel: in the time interval between 30 and 100 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 38: Comparisons between our fitted CB model AG of GRB 990510, at z=1.619, Eq. (8), with the observed optical data. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contribution of the underlying galaxy and the (in this case unobservable) associated supernova has been subtracted.

Open with DEXTER

	Figure 39: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 990510. Upper panel: the light curve at 13.68 GHz. Lower panel: the light curve at 8.6-8.7 GHz.
Open with DEXTER

	Figure 40: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 990510. Upper panel: the light curve at 4.86 GHz. Lower panel: the spectrum from radio to optical frequencies in the time interval between 1 and 6 days after burst. The highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 41: The spectrum of the AG of GRB 990510 from radio to optical frequencies. Upper panel: in the time interval between 6 and 20 days after burst. Lower panel: in the time interval between 20 and 40 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 42: Comparisons between our fitted CB model AG of GRB 990123, at z=1.600, Eq. (8), and the observed optical data. The figure shows (from top to bottom) 1000 times the K-band results, 100 times the J-band, 10 times the I-band, the R-band, 1/10 of the V-band, 1/100 of the B-band and 1/1000 of the U-band. The contributions of the underlying galaxy and an expected (but, in this case, unobservable) SN1998bw-like SN have been subtracted.

Open with DEXTER

	Figure 43: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 990123. Upper panel: the light curve at 15 GHz. Lower panel: the light curve at 8.46 GHz.
Open with DEXTER

	Figure 44: The spectrum of the AG of GRB 990123 from radio to optical frequencies. Upper panel: in the time interval between 0.1 and 1 day after burst. Lower panel: in the time interval between 1 and 3 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 45: The spectrum of the AG of GRB 990123 from radio to optical frequencies. Upper panel: in the time interval between 3 and 10 days after burst. Lower panel: in the time interval between 10 and 20 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

Figure 46: Comparisons between our fitted CB model AG of GRB 970508, at z=0.835, Eq. (8), with the observed optical data. The figure shows (from top to bottom), 10 times the I-band, the R-band, 1/10 of the V-band and 1/100 of the B-band. The contributions of the underlying galaxy and the expected SN1998bw-like SN have been subtracted. In a CB-model fit, there is in this case strong evidence for such a SN (DDD 2001).

Open with DEXTER

	Figure 47: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 970508. Upper panel: the light curve at 8.46 GHz. Lower panel: the light curve at 4.86 GHz.
Open with DEXTER

	Figure 48: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 970508. Upper panel: the light curve at 1.43 GHz. Lower panel: the spectral behaviour in the time interval between 0.12 and 6 days after burst. The highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 49: The spectrum of the AG of GRB 970508 from radio to optical frequencies. Upper panel: in the time interval between 6 and 20 days after burst. Lower panel: in the time interval between 20 and 40 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 50: The spectrum of the AG of GRB 970508 from radio to optical frequencies. Upper panel: in the time interval between 40 and 100 days after burst. Lower panel: in the time interval between 100 and 470 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 51: Comparisons between our fitted CB model afterglow of GRB 980425 at z=0.0085, Eq. (8), and its observed radio afterglow. Upper panel: the light curve at 8.64 GHz. Lower panel: the light curve at 4.80 GHz.
Open with DEXTER

	Figure 52: Comparisons between our fitted CB model afterglow, Eq. (8), and the observed radio afterglow of GRB 980425. Upper panel: the light curve at 2.49 GHz. Lower panel: the light curve at 1.38 GHz.
Open with DEXTER

	Figure 53: Comparison between the observed spectrum of the AG of GRB 980425 in the radio band and the fitted CB model spectrum. Upper panel: in the time interval between 2.5 and 20 days after burst. Lower panel: in the time interval between 20 and 40 days after burst. The highest peaking curve in the upper pannel corresponds to the later time and in the lower panel to the earlier time.
Open with DEXTER

	Figure 54: Comparison between the observed spectrum of the AG of GRB 980425 in the radio band and the fitted CB model spectrum. Upper panel: in the time interval between 40 and 70 days after burst. Lower panel: in the time interval between 70 and 150 days after burst. In both cases the highest peaking curve corresponds to the earlier time.
Open with DEXTER

	Figure 55: The late spectrum of GRB 980425 in the time interval between 150 and 759 days after burst. The highest peaking line corresponds to the earlier time. The late isolated point is the last optical observation, which must correspond to SN1998bw and not to the AG of the CB of GRB 980425.
Open with DEXTER