5 Limits

In order to set limits on the contribution of dark objects to the halo, we use the so-called "standard'' halo model described in SM98 as model 1, and take into account the efficiency of the analysis given in Sect. 3.

For a given experiment, assuming that the halo is made of compact objects having a single mass M, we define $P_{M}(t_{\rm E})$ as the probability distribution of expected event durations, taking efficiencies into account, and $f \tilde{N}_{\negthinspace M}$ as the expected number of events, where f is the halo mass fraction with respect to a full standard halo. We construct a frequentist confidence level 1-p_n considering only the number n of observed events as a Poisson process:

$$1 - p_n = \sum_{i=0}^n\frac{{\rm e}^{-f \tilde{N}_{\negthinspace M}} ( f \tilde{N}_{\negthinspace M})^i}{i!}\cdot$$

We also make an independant Kolmogorov test comparing the observed event durations to the expected $P_{M}(t_{\rm E})$ distribution, and obtain a Kolmogorov probability p_t.

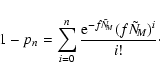
A well known prescription for the confidence level of the combined test is

$$p = p_n p_t ( 1 - \ln p_n p_t).$$

Our experiment has however an unknown contribution of background - variable stars or any other unknown phenomenon - to the observed candidates. We therefore test all combinations, attributing candidates either to signal or background, and retain, for every mass fraction f, the configuration that maximizes p, i.e. the most conservative one. This ensures that we have a given frequentist coverage for all possible hypotheses.

We then set a frequentist 95% CL limit on f, taking into account both the number of candidates and their duration, by finding the value of f that yields $p_{\rm max} = 0.05$.

Although this prescription could be used to combine several experiments, it gives the same weight to all and does not yield useful results if the sensitivities of some of the experiments differ significantly. Therefore, to combine various experiments, we use instead a Liptak-Stouffer (Liptak 1958) prescription where the flat p-values are converted to unit-variance, zero-mean Gaussian distributed variables. A weighted sum of these variables is also Gaussian distributed, and can be converted back to a p-value. We take as weights the expected number of events of each experiment for each lens mass.

The results obtained by the various phases of EROS (which are independent experiments) are summarized in Table 2 for microlensing candidates towards the SMC - no SMC candidate in EROS1 (Renault et al. 1998), 4 candidates in EROS2 ( SM98and present work) - and in table 4 for microlensing candidates towards the LMC - no planetary mass candidate (Renault et al. 1997, 1998), LMC-1 from EROS1 photographic plates (Ansari et al. 1996) and the others from EROS2 (Lasserre et al. 2000; Lasserre 2000; Milsztajn et al. 2001).

 

 

Table 4: Summary of the microlensing candidates detected by EROS towards the LMC. The parameters are the same as in Table 2.

	u0	$t_{\rm E}$
LMC-1	0.44	23
LMC-3	0.21	44
LMC-5	0.59	24
LMC-6	0.41	35
LMC-7	0.30	30

Figure 3 shows the 95% exclusion limit derived from this method on f, the halo mass fraction, at any given mass M - i.e. assuming all deflectors in the halo have mass M - for the EROS1 CCD LMC and  EROS1 CCD SMC, EROS1 photographic plates, EROS2 3-year LMC and EROS2 5-year SMC experiments, and for the combination of all. We also show in the figure the limits that would be obtained with a single SMC event ( SMC-1), then with no event at all in any of the EROS experiments, which indicates the overall sensibility of the EROS project, considering presently analysed data.

Figure 3: Exclusion diagram at 95% C.L. for the standard halo model ( $4 \times 10^{11}~M_\odot$ inside 50 kpc). The dashed lines are the limits towards the LMC by EROS 1 and EROS 2, the thin plain lines are limits towards the SMC  and the thick line is the combined limit from the five EROS sub-experiments. The dotted lines are the limits that would be obtained considering no observed events: they indicate the overall sensibility of the EROS dataset. We also indicate the limit that would be obtained if the three very long duration events on the SMC were considered as background (label " SMC-1 only''): the limit is lowered in a negligible way in the 2-3 $M_\odot$ mass range.

The "dent'' in the EROS1 plate limit and in the EROS2 LMC limit at a mass near $0.5~M_\odot$ is the impact of the $\sim$30 day candidates observed towards the LMC. For any mass between $2 \times 10^{-7}$ and $10^{-1}~{M}_\odot$, we exclude at 95% C.L. that more than 20% of the mass of a standard halo be made of compact objects. It can be seen that the combined limit is above the best limit for some values of the mass. This occurs quite naturally since the observed SMC and LMC candidates have quite different characteristics. At high mass, for instance, our method will consider SMC candidates as signal and LMC candidates as background, thus weakening the limit obtained by the LMC alone. It illustrates the (marginally significant) incompatibility between the candidates observed by EROS towards the SMC and the LMC.