4 Blending effect

The above efficiencies have been derived without taking account of stellar blending.

We have performed a study to quantify precisely the influence of blending on our results. We simulate an experiment with synthetic images, regularly spaced in time, in which microlensing events are embedded. The images are built from the HST colour-magnitude diagram (CMD) and luminosity function (LF) of the Magellanic Clouds, which extend well beyond the EROS detection limit (down to V=23.5 in the HST data). We have checked that the CMD and LF that we construct from these simulated images are in good agreement with those obtained from our data. All stars are lensed for a timescale $t_{\rm E}$ of 5 images. The impact parameter u₀ is drawn uniformly between 0 and 1.5, and t₀ is set so that no two stars less than 20 pixels apart are magnified simultaneously (typical EROS images have a seeing of 2.1 arcsec corresponding to a Gaussian with rms of 1.5 pixel).

The standard photometry chain of EROS is applied to these images, leading to the detection of 5599 objects (in this terminology an object usually encompasses several simulated stars) with their red and blue light curves. A total of 6304 generated microlensing events were found with u₀<1 and an average timescale $\langle t_{\rm E} \rangle = 3.16$ images. The effect of blending is readily seen from the fact that more events than objects are detected. Of these events, 60% are due to the brightest star in the two pixels around the object, with recovered $\langle t_{\rm E} \rangle = 4.00$ images and $\langle u_0\rangle = 0.52$, close to the generated values. The remaining events are due to a fainter, blended component of the object, with recovered $\langle t_{\rm E} \rangle = 1.89$ images, well underestimated, and $\langle u_0 \rangle = 0.64$, clearly overestimated, as expected from the impact of a significant blend. The optical depth being proportional to the number of events and to their mean $t_{\rm E}$, an estimate of the ratio R of the recovered optical depth to the generated one is:

$$R = \frac{6304}{5599/1.5}\frac{3.16}{5.0} = 1.07,$$

with an estimated error of about 10%.

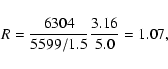
The light curves from the above blending simulation are then used as templates in our Monte Carlo chain designed to compute the efficiency of our analysis (Sect. 3) as follows: for each object detected in the actual data, an object is randomly chosen from the blending simulation in the same region of the CMD. The light curve of the latter is shifted and stretched to account for the randomly selected duration and time of maximum amplification, but the amplitudes in each colour are of course kept as found in the blending simulation to reflect the impact of the underlying stellar companions of the microlensed star. This template is used (instead of the standard shape derived by Paczynski in the absence of blending and used for the efficiency computation in the previous section) to add a microlensing event to the real (flat in most cases) light curve. To ensure similar photometric dispersion in the Monte Carlo and in the data, the rms flux deviation of each simulated data point from the blended microlensing light curve is taken to be the same as the deviation of the real light curve from constant brightness. The modified light curve goes through the same analysis cuts as in the standard computation of the efficiency.

The efficiency with the blending simulation described above is within 10% of the efficiency computed from the standard procedure, in agreement with estimates in previous works (Palanque-Delabrouille 1997). The loss due to the under-estimation of the magnification of a blended event (the observed magnification on a blended object is lower than the physical magnification of the underlying star) is almost exactly compensated by the fact that an object includes more than one star subject to lensing. In addition, as expected, the cuts of the analysis are sufficiently loose not to reject blended microlensing events. In particular, there are no cuts requiring a strict achromaticity of the event. For the EROS experiment, blending has a small impact on the efficiency and can therefore be neglected.