A&A 400, 1183-1198 (2003)
DOI: 10.1051/0004-6361:20030030
F. Patat
European Southern Observatory, K. Schwarzschild Str. 2, 85748 Garching, Germany
Received 24 October 2002 / Accepted 19 December 2002
Abstract
In this paper we present and discuss for the first time a large data set
of UBVRI night sky brightness measurements collected at ESO-Paranal from
April 2000 to September 2001. A total of about 3900 images obtained on 174
different nights with FORS1 were analysed using an automatic algorithm
specifically designed for this purpose. This led to the construction of
an unprecedented database that allowed us to study in detail a number of
effects such as differential zodiacal light contamination, airmass dependency,
daily solar activity and moonlight contribution. Particular care was
devoted to the investigation of short time scale variations and micro-auroral
events. The typical dark time night sky brightness values found for Paranal
are similar to those reported for other astronomical dark sites at a similar
solar cycle phase. The zenith-corrected values averaged over the whole period
are 22.3, 22.6, 21.6 20.9 and 19.7 mag arcsec-2 in
U, B, V, R and I
respectively. In particular, there is no evidence of light pollution either
in the broadband photometry or in the high-airmass spectra we have analysed.
Finally, possible applications for the exposure time calculators are
discussed.
Key words: atmospheric effects - site testing - light pollution - techniques: photometric
The night sky brightness, together with number of clear nights, seeing, transparency, photometric stability and humidity, are some of the most important parameters that qualify a site for front-line ground-based astronomy. While there is almost no way to control the other characteristics of an astronomical site, the sky brightness can be kept at its natural level by preventing light pollution in the observatory areas. This can be achieved by means of extensive monitoring programmes aimed at detecting any possible effects of human activity on the measured sky brightness.
For this purpose, we have started an automatic survey of the UBVRI night sky brightness at Paranal with the aim of both getting for the first time values for this site and building a large database. The latter is a fundamental step for the long term trend which, given the possible growth of human activities around the observatory, will allow us to check the health of Paranal's sky in the years to come.
The ESO-Paranal Observatory is located on the top of Cerro Paranal in the
Atacama Desert in the northern part of Chile, one of the driest areas on
Earth. Cerro Paranal (2635 m, 24![]() 40
40![]() S,
70
S,
70![]() 25
25![]() W) is at about 108 km S of Antofagasta
(225,000 inhabitants; azimuth 0°.2), 280 km SW from Calama
(121 000 inhabitants; azimuth 32°.3), 152 km WSW from La Escondida
(azimuth 32°.9), 23 km NNW from a small mining
plant (Yumbes, azimuth 157°.7) and 12 km inland from the Pacific Coast.
This ensures that the astronomical observations to be carried out there
are not disturbed by adverse human activities like dust and light from
cities and roads. Nevertheless, a systematic monitoring of the
sky conditions is mandatory in order to preserve the high site quality
and to take appropriate action, if the conditions are proven to
deteriorate. Besides this, it will also set the stage for the study of
natural sky brightness oscillations, both on short and long time scales,
such as micro-auroral activity, seasonal and sunspot cycle effects.
W) is at about 108 km S of Antofagasta
(225,000 inhabitants; azimuth 0°.2), 280 km SW from Calama
(121 000 inhabitants; azimuth 32°.3), 152 km WSW from La Escondida
(azimuth 32°.9), 23 km NNW from a small mining
plant (Yumbes, azimuth 157°.7) and 12 km inland from the Pacific Coast.
This ensures that the astronomical observations to be carried out there
are not disturbed by adverse human activities like dust and light from
cities and roads. Nevertheless, a systematic monitoring of the
sky conditions is mandatory in order to preserve the high site quality
and to take appropriate action, if the conditions are proven to
deteriorate. Besides this, it will also set the stage for the study of
natural sky brightness oscillations, both on short and long time scales,
such as micro-auroral activity, seasonal and sunspot cycle effects.
The night sky radiation has been studied by several authors, starting with the pioneering work by Lord Rayleigh in the 1920s. For thorough reviews on this subject the reader is referred to the classical textbook by Roach & Gordon (1973) and the recent extensive work by Leinert et al. (1998), which explore a large number of aspects connected with the study of the night sky emission. In the following, we will give a short introduction to the subject, concentrating on the optical wavelengths only.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f1.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg15.gif) |
Figure 1:
Night sky spectrum obtained at Paranal
on February 25, 2001 02:38UT in the spectral region covered by
B, V, R and I passbands (from top to bottom). The original
FORS1 1800 s frame was taken at 1.42 airmasses with a long slit of
1
|
| Open with DEXTER | |
The night sky light as seen from ground is generated by several sources, some of which are of extra-terrestrial nature (e.g. unresolved stars/galaxies, diffuse galactic background, zodiacal light) and others are due to atmospheric phenomena (airglow and auroral activity in the upper Earth's atmosphere). In addition to these natural components, human activity has added an extra source, namely the artificial light scattered by the troposphere, mostly in the form of Hg-Na emission lines in the blue-visible part of the optical spectrum (vapour lamps) and a weak continuum (incandescent lamps). While the extra-terrestrial components vary only with the position on the sky and are therefore predictable, the terrestrial ones are known to depend on a large number of parameters (season, geographical position, solar cycle and so on) which interact in a largely unpredictable way. In fact, airglow contributes with a significant fraction to the optical global night sky emission and hence its variations have a strong effect on the overall brightness.
To illustrate the various processes which contribute to the
airglow at different wavelengths, in Fig. 1 we have plotted
a high signal-to-noise, flux calibrated night sky spectrum obtained at Paranal
on a moonless night (2001, Feb. 25) at a zenith distance of 45![]() ,
about two hours after the end of evening astronomical twilight. In the B band the spectrum is rather featureless and it is characterised by the
so called airglow pseudo-continuum, which arises in layers at a height of
about 90-100 km (mesopause). This actually extends from 4000 Å to 7000 Å and its intensity is of the order of 3
,
about two hours after the end of evening astronomical twilight. In the B band the spectrum is rather featureless and it is characterised by the
so called airglow pseudo-continuum, which arises in layers at a height of
about 90-100 km (mesopause). This actually extends from 4000 Å to 7000 Å and its intensity is of the order of 3![]() 10-7 erg s-1 cm-2 Å-1 sr-1 at 4500 Å. All visible emission
features, which become particularly marked below 4000 Å
and largely dominate the U passband (not included in the plots),
are due to Herzberg and Chamberlain O2 bands (Broadfoot & Kendall 1968).
In light polluted sites, this spectral region is characterised by the
presence of Hg I (3650, 3663, 4047, 4078, 4358 and 5461 Å) and NaI (4978,
4983, 5149 and 5153 Å) lines (see for example Osterbrock & Martel 1992)
which are, if any, very weak in the spectrum of Fig. 1
(see Sect. 9 for a discussion on light pollution at
Paranal). Some of these lines are clearly visible in spectra taken, for
example, at La Palma (Benn & Ellison 1998, Fig. 1) and Calar Alto
(Leinert et al. 1995, Figs. 7 and 8).
10-7 erg s-1 cm-2 Å-1 sr-1 at 4500 Å. All visible emission
features, which become particularly marked below 4000 Å
and largely dominate the U passband (not included in the plots),
are due to Herzberg and Chamberlain O2 bands (Broadfoot & Kendall 1968).
In light polluted sites, this spectral region is characterised by the
presence of Hg I (3650, 3663, 4047, 4078, 4358 and 5461 Å) and NaI (4978,
4983, 5149 and 5153 Å) lines (see for example Osterbrock & Martel 1992)
which are, if any, very weak in the spectrum of Fig. 1
(see Sect. 9 for a discussion on light pollution at
Paranal). Some of these lines are clearly visible in spectra taken, for
example, at La Palma (Benn & Ellison 1998, Fig. 1) and Calar Alto
(Leinert et al. 1995, Figs. 7 and 8).
The V passband is chiefly dominated by [OI]5577 Å and to a lesser extent by NaI D and [OI]6300, 6364 Å doublet. In the spectrum of Fig. 1 the relative contribution to the total flux of these three lines is 0.17, 0.03 and 0.02, respectively. Besides the aforementioned pseudo-continuum, several OH Meinel vibration-rotation bands are also present in this spectral window (Meinel 1950); in particular, OH(8-2) is clearly visible on the red wing of NaI D lines and OH(5-0), OH(9-3) on the blue wing of [OI]6300 Å. All these features are known to be strongly variable and show independent behaviour (see for example the discussion in Benn & Ellison 1998), probably due to the fact that they are generated in different atmospheric layers (Leinert et al. 1998 and references therein). In fact, [OI]5577 Å, which is generally the brightest emission line in the optical sky spectrum, arises in layers at an altitude of 90 km, while [OI]6300, 6364 Å is produced at 250-300 km. The OH bands are emitted by a layer at about 85 km, while the Na ID is generated at about 92 km, in the so called Sodium-layer which is used by laser guide star adaptive optic systems. In particular, [OI]6300, 6364 Å shows a marked and complex dependency on geomagnetic latitude which turns into different typical line intensities at different observatories (Roach & Gordon 1973). Moreover, this doublet undergoes abrupt intensity changes (Barbier 1957); an example of such an event is reported and discussed in Sect. 9.
In the R passband, besides the contribution of NaI D and [OI]6300, 6364 Å,
which account for 0.03 and 0.10 of the total flux in the spectrum of
Fig. 1, strong OH Meinel bands like OH(7-2), OH(8-3),
OH(4-0), OH(9-4) and OH(5-1) begin to appear, while the pseudo-continuum
remains constant at about 3![]() 10-7 erg s-1 cm-2 Å-1 sr-1. Finally, the I passband is dominated by the
Meinel bands OH(8-3), OH(4-0), OH(9-4), OH(5-1) and OH(6-2); the broad
feature visible at 8600-8700 Å, and marginally contributing to the
I flux, is the blend of the R and P branches of O2(0-1) (Broadfoot
& Kendall 1968).
10-7 erg s-1 cm-2 Å-1 sr-1. Finally, the I passband is dominated by the
Meinel bands OH(8-3), OH(4-0), OH(9-4), OH(5-1) and OH(6-2); the broad
feature visible at 8600-8700 Å, and marginally contributing to the
I flux, is the blend of the R and P branches of O2(0-1) (Broadfoot
& Kendall 1968).
Several sky brightness surveys have been performed at a number of
observatories in the world, most of the time in B and V passbands
using small telescopes coupled to photo-multipliers.
A comprehensive list of published data is given by Benn & Ellison
(1998).
All authors agree on the fact that the dark time sky brightness shows
strong variations within the same night on the time scales
of tens of minutes to hours. This variation is
commonly attributed to airglow fluctuations. Moreover, as first pointed
out by Rayleigh (1928), the intensity of the [OI]5577 Å
line depends on the solar activity. Similar results were found for other
emission lines (NaI D and OH) by Rosenberg & Zimmerman (1967).
Walker (1988b) found that B and V sky brightness is well
correlated with the 10.7 cm solar radio flux and reported a range of
![]() 0.5 mag in B and V during a full sunspot cycle.
Similar values were found by Krisciunas (1990), Leinert et al. (1995) and Mattila et al. (1996), so that the effect
of solar activity is commonly accepted (Leinert et al. 1998).
For this reason, when comparing sky brightness measurements, one should
also keep in mind the time when they were obtained with respect to the
solar cycle, since the difference can be substantial.
A matter of long debate has been the so-called Walker effect,
named after Walker (1988b), who reported a steady exponential
decrease of
0.5 mag in B and V during a full sunspot cycle.
Similar values were found by Krisciunas (1990), Leinert et al. (1995) and Mattila et al. (1996), so that the effect
of solar activity is commonly accepted (Leinert et al. 1998).
For this reason, when comparing sky brightness measurements, one should
also keep in mind the time when they were obtained with respect to the
solar cycle, since the difference can be substantial.
A matter of long debate has been the so-called Walker effect,
named after Walker (1988b), who reported a steady exponential
decrease of ![]() 0.4 mag in the night sky brightness during the first six
hours following the end of twilight. This finding has been questioned by
several authors. We address this issue in detail later
(Sect. 6 and Appendix D).
0.4 mag in the night sky brightness during the first six
hours following the end of twilight. This finding has been questioned by
several authors. We address this issue in detail later
(Sect. 6 and Appendix D).
Here we present for the first time UBVRI sky brightness measurements for Paranal, obtained on 174 nights from 2000 April 20 to 2001 September 23 which, to our knowledge, makes it the largest homogeneous data set available. Being produced by an automatic procedure, this data base is continuously growing and it will provide an unprecedented chance to investigate both the long term evolution of the night sky quality and to study in detail the short time scale fluctuations which are still under debate.
The paper is organized as follows. After giving some information on the basic data reduction procedure in Sect. 2, in Sect. 3 we discuss the photometric calibration and error estimates, while the general properties of our night sky brightness survey are described in Sect. 4. The results obtained during dark time are then presented in Sect. 5 and the short time-scale variations are analysed in Sect. 6. In Sect. 7 we compare our data obtained in bright time with the model by Krisciunas & Schaefer (1991) for the effects of moonlight, while the dependency on solar activity is investigated in Sect. 8. In Sect. 9 we discuss the results and summarize our conclusions. Finally, detailed discussions about some of the topics are given in Appendices A-D.
The data set discussed in this work has been obtained with the FOcal
Reducer/low dispersion Spectrograph (hereafter FORS1), mounted
at the Cassegrain focus of ESO-Antu/Melipal 8.2 m telescopes
(Szeifert 2002). The instrument is
equipped with a
![]() pixels (px) TK2048EB4-1 backside thinned
CCD and has two remotely exchangeable collimators, which give a projected
scale of 0
pixels (px) TK2048EB4-1 backside thinned
CCD and has two remotely exchangeable collimators, which give a projected
scale of 0
![]() 2 and 0
2 and 0
![]() 1 per pixel (24
1 per pixel (24 ![]() m
m ![]() 24
24 ![]() m). According
to the used collimator, the sky area covered by the detector is
m). According
to the used collimator, the sky area covered by the detector is
![]() and
and
![]() ,
respectively. Most of the
observations discussed in this paper were performed with the lower resolution
collimator, since the higher resolution is used only to exploit excellent
seeing conditions (FWHM
,
respectively. Most of the
observations discussed in this paper were performed with the lower resolution
collimator, since the higher resolution is used only to exploit excellent
seeing conditions (FWHM ![]() 0
0
![]() 4).
4).
In the current operational scheme, FORS1 is offered roughly in equal fractions between visitor mode (VM) and service mode (SM). While VM data are immediately released to the visiting astronomers, the SM data are processed by the FORS-Pipeline and then undergo a series of quality control (QC) checks before being delivered to the users. In particular, the imaging frames are bias and flat-field corrected and the resulting products are analysed in order to assess the accuracy of the flat-fielding, the image quality and so on. The sky background measurement was experimentally introduced in the QC procedures starting with April 2000. Since then, each single imaging frame obtained during SM runs is used to measure the sky brightness. During the first eighteen months of sky brightness monitoring, more than 4500 frames taken with broad and narrow band filters have been analysed.
As already mentioned, all imaging frames are automatically bias and flat
field corrected by the FORS pipeline.
This is a fundamental step, since in the case of imaging, the FORS1 detector
is readout using four amplifiers which have different gains. The bias and
flat field correction remove the four-port structure to within ![]() 1
electron. This has to be compared with the rms read-out noise (RON), which is
5.5 and 6.3 electrons in the high gain and low gain modes respectively.
Moreover, due to the large collecting area of the telescope, FORS1 imaging
frames become sky background dominated already after less than two minutes.
The only significant exception is the U passband, where background
domination occurs after more than 10 min (see also Table 1).
The dark current
of FORS1 detector is
1
electron. This has to be compared with the rms read-out noise (RON), which is
5.5 and 6.3 electrons in the high gain and low gain modes respectively.
Moreover, due to the large collecting area of the telescope, FORS1 imaging
frames become sky background dominated already after less than two minutes.
The only significant exception is the U passband, where background
domination occurs after more than 10 min (see also Table 1).
The dark current
of FORS1 detector is ![]() 2.2
2.2 ![]() 10-3 e- s-1 px-1
(Szeifert 2002) and hence its contribution to the background can
be safely neglected.
10-3 e- s-1 px-1
(Szeifert 2002) and hence its contribution to the background can
be safely neglected.
| Passband | Count Rate | t3 |
| (e- px-1 s-1) | (s) | |
| U | 0.5 | 714 |
| B | 3.8 | 94 |
| V | 15.8 | 23 |
| R | 26.7 | 13 |
| I | 32.1 | 11 |
Since the flat fielding is performed using twilight sky flats, some large scale gradients are randomly introduced by the flat fielding process; maximum peak-to-peak residual deviations are of the order of 6%. Finally, small scale features are very well removed, the only exceptions being some non-linear pixels spread across the detector.
The next step in the process is the estimate of the sky background. Since the science frames produced by FORS1 are, of course, not necessarily taken in empty fields, the background measurement requires a careful treatment. For this purpose we have designed a specific algorithm, which is presented and discussed in Patat (2003). The reader is referred to that paper for a detailed description of the problem and the technique we have adopted to solve it.
Once the sky background
![]() has been estimated, the flux per
square arcsecond and per unit time is given by
has been estimated, the flux per
square arcsecond and per unit time is given by
![]() ,
where p is the detector's scale (arcsec pix-1) and
,
where p is the detector's scale (arcsec pix-1) and
![]() is
the exposure time (in seconds). The instrumental sky surface brightness
is then defined as
is
the exposure time (in seconds). The instrumental sky surface brightness
is then defined as
The next step one needs to perform to get the final sky surface brightness
is to convert the instrumental magnitudes to the standard UBVRI photometric
system. Following the prescriptions by Pilachowski et al. (1989),
the sky brightness is calibrated without correcting the measured flux by
atmospheric extinction, since the effect is actually taking place mostly
in the atmosphere itself. This is of course not true for the
contribution coming from faint stars, galaxies and the zodiacal light, which
however account for a minor fraction of the whole effect, airglow being the
prominent source of night sky emission in dark astronomical sites.
The reader is referred to Krisciunas (1990) for a more detailed
discussion of this point; here we add only that this practically
corresponds to set to zero the airmass of the observed sky area in the
calibration equation. Therefore, if
![]() ,
,
![]() are the calibrated
and instrumental sky magnitudes, M*, m* are the corresponding values
for a photometric standard star observed at airmass z*, and
are the calibrated
and instrumental sky magnitudes, M*, m* are the corresponding values
for a photometric standard star observed at airmass z*, and ![]() is
the extinction coefficient, we have that
is
the extinction coefficient, we have that
![]()
![]() .
This
relation can be rewritten in a more general way as
.
This
relation can be rewritten in a more general way as
![]() ,
where m0 is the photometric
zeropoint in a given passband and
,
where m0 is the photometric
zeropoint in a given passband and ![]() is the colour term in that
passband for the color
is the colour term in that
passband for the color
![]() .
For example, in the case of B filter,
this relation can be written as
.
For example, in the case of B filter,
this relation can be written as
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f2.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg37.gif) |
Figure 2: UBVRI photometric zeropoints for FORS1 during the time range covered by sky brightness measurements presented in this work (vertical dotted lines). The thick segments plotted on the lower diagram indicate the presence of sky brightness data, while the arrows in the upper part of the figure correspond to some relevant events. A) water condensation on main mirror of UT1-Antu. B) UT1-Antu main mirror re-aluminisation after the water condensation event. C) FORS1 moved from UT1-Antu to UT3-Melipal. Plotted zeropoints have been corrected for extinction and colour terms using average values (see Appendix A). |
| Open with DEXTER | |
In the case of FORS1, observations of
photometric standard fields (Landolt 1992) are regularly obtained as part
of the calibration plan; typically one to three fields are observed during
each service mode night. The photometric zeropoints were derived from these
observations by means of a semi-automatic procedure, assuming constant
extinction coefficients and colour terms. For a more detailed discussion on
these parameters, the reader is referred to Appendix A,
where we show that this is a reasonable assumption.
Figure 2 shows that, with the exception of a few cases,
Paranal is photometrically stable, being the rms zeropoint fluctuation
![]() 0.03 mag in U and
0.03 mag in U and
![]() 0.02 mag in all other
passbands.
Three clear jumps are visible in Fig. 2, all basically
due to physical changes in the main mirror of the telescope. Besides
these sudden variations, we have detected a slow decrease in the efficiency
which is clearly visible in the first 10 months and is most probably
due to aluminium oxidation and dust deposition. The efficiency loss
appears to be linear in time, with a rate steadily decreasing from blue to
red passbands, being 0.13 mag yr-1 in U and 0.05 mag yr-1 in I.
To allow for a proper compensation of these effects, we have divided the whole
time range in four different periods, in which we have used a linear least
squares fit to the zero points obtained in each band during photometric nights
only. This gives a handy description of the overall system efficiency which
is easy to implement in an automatic calibration procedure.
0.02 mag in all other
passbands.
Three clear jumps are visible in Fig. 2, all basically
due to physical changes in the main mirror of the telescope. Besides
these sudden variations, we have detected a slow decrease in the efficiency
which is clearly visible in the first 10 months and is most probably
due to aluminium oxidation and dust deposition. The efficiency loss
appears to be linear in time, with a rate steadily decreasing from blue to
red passbands, being 0.13 mag yr-1 in U and 0.05 mag yr-1 in I.
To allow for a proper compensation of these effects, we have divided the whole
time range in four different periods, in which we have used a linear least
squares fit to the zero points obtained in each band during photometric nights
only. This gives a handy description of the overall system efficiency which
is easy to implement in an automatic calibration procedure.
| Site | Year | U-B | B-V | V-R | V-I | Reference |
| Cerro Tololo | 1987-8 | -0.7 | +0.9 | +0.9 | +1.9 | Walker (1987, 1988a) |
| La Silla | 1978 | - | +1.1 | +0.9 | +2.3 | Mattila et al. (1996) |
| Calar Alto | 1990 | -0.5 | +1.1 | +0.9 | +2.8 | Leinert et al. (1995) |
| La Palma | 1994-6 | -0.7 | +0.8 | +0.9 | +1.9 | Benn & Ellison (1998) |
| Paranal | 2000-1 | -0.4 | +1.0 | +0.8 | +1.9 | this work |
To derive the colour correction included in the calibration equation one needs
to know the sky colours
![]() .
In principle
.
In principle
![]() can be computed
from the instrumental magnitudes, provided that the data which correspond
to the two passbands used for the given colour are taken closely in time.
In fact, the sky brightness is known to have quite a strong time evolution
even in moonless nights and far from twilight (Walker 1988b; Pilachowski et al. 1989; Krisciunas 1990; Leinert et al. 1998) and using magnitudes obtained
in different conditions would lead to wrong colours. On the other hand, very
often FORS1 images are taken in rather long sequences, which make use of
the same filter; for this very reason it is quite rare to have
close-in-time multi-band observations. Due to this fact and to allow for a
general and uniform approach, we have decided to use constant sky colours for the
colour correction. In fact, the colour terms are small, and even large errors on
the colours produce small variations in the corresponding colour correction.
can be computed
from the instrumental magnitudes, provided that the data which correspond
to the two passbands used for the given colour are taken closely in time.
In fact, the sky brightness is known to have quite a strong time evolution
even in moonless nights and far from twilight (Walker 1988b; Pilachowski et al. 1989; Krisciunas 1990; Leinert et al. 1998) and using magnitudes obtained
in different conditions would lead to wrong colours. On the other hand, very
often FORS1 images are taken in rather long sequences, which make use of
the same filter; for this very reason it is quite rare to have
close-in-time multi-band observations. Due to this fact and to allow for a
general and uniform approach, we have decided to use constant sky colours for the
colour correction. In fact, the colour terms are small, and even large errors on
the colours produce small variations in the corresponding colour correction.
For this purpose we have used color-uncorrected sky brightness values obtained
in dark time, at airmass ![]() and at a time distance from the twilights
and at a time distance from the twilights
![]() hours and estimated the typical value as the average.
The corresponding colours are shown in Table 2, where they are
compared with those obtained at other observatories. As one can see, B-Vand V-R show a small scatter between different observatories, while U-B
and V-I are rather dispersed.
In particular, V-I spans almost a magnitude, the value reported for Calar
Alto being the reddest. This is due to the fact that the Calar Alto sky in Iappears to be definitely brighter than in all other listed sites.
hours and estimated the typical value as the average.
The corresponding colours are shown in Table 2, where they are
compared with those obtained at other observatories. As one can see, B-Vand V-R show a small scatter between different observatories, while U-B
and V-I are rather dispersed.
In particular, V-I spans almost a magnitude, the value reported for Calar
Alto being the reddest. This is due to the fact that the Calar Alto sky in Iappears to be definitely brighter than in all other listed sites.
Now, given the color terms reported in Table A.2, the color
corrections
![]() turn out to be -0.02
turn out to be -0.02 ![]() 0.02,
-0.09
0.02,
-0.09 ![]() 0.02, +0.04
0.02, +0.04 ![]() 0.01, +0.02
0.01, +0.02 ![]() 0.01 and -0.08
0.01 and -0.08 ![]() 0.02 in U,
B, V, R and I respectively. The uncertainties were estimated from the
dispersion on the computed average colours, which is
0.02 in U,
B, V, R and I respectively. The uncertainties were estimated from the
dispersion on the computed average colours, which is
![]() 0.3 for all
passbands.
We emphasize that this rather large value is not due to measurement errors,
but rather to the strong intrinsic variations shown by the sky brightness,
which we will discuss in detail later on. We also warn the reader that the
colour corrections computed assuming dark sky colours are not necessarily
correct under other conditions, when the night sky emission is strongly
influenced by other sources, like Sun and moon. At any rate, colour
variations of 1 mag would produce a change in the calibrated magnitude of
0.3 for all
passbands.
We emphasize that this rather large value is not due to measurement errors,
but rather to the strong intrinsic variations shown by the sky brightness,
which we will discuss in detail later on. We also warn the reader that the
colour corrections computed assuming dark sky colours are not necessarily
correct under other conditions, when the night sky emission is strongly
influenced by other sources, like Sun and moon. At any rate, colour
variations of 1 mag would produce a change in the calibrated magnitude of
![]() 0.1 mag in the worst case.
0.1 mag in the worst case.
Due to the increased depth of the emitting layers, the sky becomes inherently
brighter for growing zenith distances (see for example Garstang 1989;
Leinert et al. 1998). In order to compare and/or combine together sky brightness
estimates obtained at different airmasses, one needs to take into account this
effect. The law we have adopted for the airmass compensation and its ability
to reproduce the observed data are discussed in Appendix C
(see Eq. (C.3)).
After including this correction in the calibration equation and neglecting
the error on X, we have computed the global rms error on the estimated sky
brightness in the generic passband as follows:
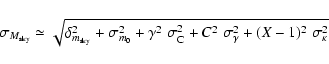 |
(2) |
The results we will discuss have been obtained between April 1 2000
and September 30 2001, corresponding to ESO Observing Periods 65, 66 and 67,
and include data obtained on 174 different nights.
During these eighteen months, 4439 images taken in the UBVRI
passbands and processed by the FORS pipeline were analysed and 3883 of them
(![]() 88%) were judged to be suitable for sky brightness measurements,
according to the criteria we have discussed in Patat (2003).
The numbers for the different passbands are shown in Table 3,
where we have reported the total number
88%) were judged to be suitable for sky brightness measurements,
according to the criteria we have discussed in Patat (2003).
The numbers for the different passbands are shown in Table 3,
where we have reported the total number ![]() of examined frames, the number
of examined frames, the number
![]() of frames which passed the tests and the percentage of success
of frames which passed the tests and the percentage of success ![]() .
As expected, this is particularly poor for the U filter, where the sky
background level is usually very low. In fact, we have shown that practically
all frames with a sky background level lower than 400 electrons are rejected
(Patat 2003, Sect. 5).
Since to reach this level in the U passband one needs to expose for more
than 800 s (see Table 1), this explains the large
fraction of unacceptable frames.
We also note that the number of input frames in the various filters reflects
the effective user's requests. As one can see from Table 3, the
percentage of filter usage
.
As expected, this is particularly poor for the U filter, where the sky
background level is usually very low. In fact, we have shown that practically
all frames with a sky background level lower than 400 electrons are rejected
(Patat 2003, Sect. 5).
Since to reach this level in the U passband one needs to expose for more
than 800 s (see Table 1), this explains the large
fraction of unacceptable frames.
We also note that the number of input frames in the various filters reflects
the effective user's requests. As one can see from Table 3, the
percentage of filter usage ![]() steadily grows going from blue to red
filters, with R and I used in almost 70% of the cases, while the U
filter is extremely rarely used.
steadily grows going from blue to red
filters, with R and I used in almost 70% of the cases, while the U
filter is extremely rarely used.
| Filter | ||||
| U | 1.8 | 204 | 68 | 33.3 |
| B | 11.3 | 479 | 434 | 90.6 |
| V | 17.3 | 845 | 673 | 79.6 |
| R | 27.1 | 1128 | 1055 | 93.5 |
| I | 42.5 | 1783 | 1653 | 92.7 |
| 4439 | 3883 | 87.5 |
To allow for a thorough analysis of the data, the sky brightness measurements
have been logged together with a large set of parameters, some of which are
related to the target's position and others to the ambient conditions.
The first set has been computed using routines adapted from those coded by J. Thorstensen![]() and it includes average airmass, azimuth, galactic longitude and latitude,
ecliptic latitude and helio-ecliptic longitude,
target-moon angular distance, moon elevation, fractional lunar illumination
(FLI), target-Sun angular distance, Sun elevation and time distance between
observation and closest twilight. Additionally we have implemented two
routines to compute the expected moon brightness and zodiacal light
contribution at target's position.
For the first task we have adopted the model by Krisciunas & Schaefer
(1991) and its generalisation to UBVRI passbands (Schaefer 1998),
while for the zodiacal light we have applied a bi-linear interpolation to
the data presented by Levasseur-Regourd & Dumont (1980). The
original data is converted from S10(V) to cgs units and the UBRI
brightness is computed from the V values reported by Levasseur-Regourd &
Dumont assuming a solar spectrum, which is a good approximation in the
wavelength range 0.2-2
and it includes average airmass, azimuth, galactic longitude and latitude,
ecliptic latitude and helio-ecliptic longitude,
target-moon angular distance, moon elevation, fractional lunar illumination
(FLI), target-Sun angular distance, Sun elevation and time distance between
observation and closest twilight. Additionally we have implemented two
routines to compute the expected moon brightness and zodiacal light
contribution at target's position.
For the first task we have adopted the model by Krisciunas & Schaefer
(1991) and its generalisation to UBVRI passbands (Schaefer 1998),
while for the zodiacal light we have applied a bi-linear interpolation to
the data presented by Levasseur-Regourd & Dumont (1980). The
original data is converted from S10(V) to cgs units and the UBRI
brightness is computed from the V values reported by Levasseur-Regourd &
Dumont assuming a solar spectrum, which is a good approximation in the
wavelength range 0.2-2 ![]() m (Leinert et al. 1998). For this purpose
we have adopted the Sun colours reported by Livingston (2000),
which turn into the following U, B, R and I zodiacal light
intensities normalised to the V passband: 0.52, 0.94, 0.77 and 0.50.
For a derivation of the conversion factor from S10(V) to cgs units,
see Appendix B.
m (Leinert et al. 1998). For this purpose
we have adopted the Sun colours reported by Livingston (2000),
which turn into the following U, B, R and I zodiacal light
intensities normalised to the V passband: 0.52, 0.94, 0.77 and 0.50.
For a derivation of the conversion factor from S10(V) to cgs units,
see Appendix B.
The ambient conditions were retrieved from the VLT Astronomical Site Monitor
(ASM, Sandrock et al. 2000). For our purposes we have included air
temperature, relative humidity, air pressure, wind speed and wind direction,
averaging the ASM entries across the exposure time.
Finally, to allow for further quality selections, for each sky brightness
entry we have logged the number of sub-windows which passed the ![]() -test
(see Patat 2003) and the final number
-test
(see Patat 2003) and the final number ![]() of selected sub-windows
effectively used for the background estimate.
of selected sub-windows
effectively used for the background estimate.
Throughout this paper the sky brightness is expressed in mag arcsec-2,
following common astronomical practice. However, when
one is to correct for other effects (like zodiacal light or scattered moon
light), it is more practical to use a linear unit. For this purpose, when
required, we have adopted the cgs system, where the sky brightness is
expressed in erg s-1 cm-2 Å-1 sr-1. In these units the
typical sky brightness varies in the range
10
-9-10-6 (see also Appendix B). It is natural to
introduce a surface brightness unit (sbu) defined as
1 sbu ![]() 10-9 erg s-1 cm-2 Å-1 sr-1. In the
rest of the paper we will use this unit to express the sky brightness in a
linear scale.
10-9 erg s-1 cm-2 Å-1 sr-1. In the
rest of the paper we will use this unit to express the sky brightness in a
linear scale.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f3.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg56.gif) |
Figure 3: Distribution of telescope pointings in Alt-Az coordinates. The lower left insert shows the airmass distribution. |
| Open with DEXTER | |
Due to the large number of measurements, the data give a good coverage of many relevant parameters. This is fundamental, if one is to investigate possible dependencies. In the next sub-sections we describe the statistical properties of our data set with respect to these parameters, whereas their correlations are discussed in Sects. 5-8.
The telescope pointings are well distributed in azimuth and elevation, as it
is shown in Fig. 3. In particular, they span a good range in
airmass, with a few cases reaching zenith distances larger than 60![]() .
Due to the Alt-Az mount of the VLT, the region close to zenith is not
observable, while for safety reasons the telescope does not point at zenith
distances larger than 70
.
Due to the Alt-Az mount of the VLT, the region close to zenith is not
observable, while for safety reasons the telescope does not point at zenith
distances larger than 70![]() .
Apart from these two avoidance areas, the
Alt-Az space is well sampled, at least down to zenith distances
Z= 50
.
Apart from these two avoidance areas, the
Alt-Az space is well sampled, at least down to zenith distances
Z= 50![]() .
At higher airmasses the western side of the sky appears to
be better sampled, due to the fact that the targets are sometimes followed
well after the meridian, while the observations tend to start when
they are on average at higher elevation.
.
At higher airmasses the western side of the sky appears to
be better sampled, due to the fact that the targets are sometimes followed
well after the meridian, while the observations tend to start when
they are on average at higher elevation.
Since sky brightness is expected to depend on the observed position with
respect to the Galaxy and the Ecliptic (see Leinert et al. 1998 for an
extensive review), it is interesting to see how our measurements are
distributed in these two coordinate systems. Due to the kind of scientific
programmes which are usually carried out with FORS1, we expect that most
of the observations are performed far from the galactic plane. This is
confirmed by the left panel of Fig. 4, where we have plotted
the galactic coordinates distribution of the 3883 pointings included in our
data set. As one can see, the large majority of the points lie at
|b|> 10![]() ,
and therefore the region close to the galactic plane is
not well enough sampled to allow for a good study of the sky brightness
behaviour in that area.
,
and therefore the region close to the galactic plane is
not well enough sampled to allow for a good study of the sky brightness
behaviour in that area.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f4.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg57.gif) |
Figure 4: Distribution of telescope pointings in galactic (left panel) and helio-ecliptic (right panel) coordinates. The two histograms show the distribution of galactic and ecliptic latitudes. |
| Open with DEXTER | |
The scenario is different if we consider the helio-ecliptic coordinate system
(Fig. 4, right panel). The observations are well distributed
across the ecliptic plane for
![]() 60
60![]() and
and
![]() +30
+30![]() ,
where the contribution of the zodiacal light to the
global sky brightness can be significant. As a matter of fact, the
large majority of the observations have been carried out in the range
-30
,
where the contribution of the zodiacal light to the
global sky brightness can be significant. As a matter of fact, the
large majority of the observations have been carried out in the range
-30
![]() 30
30![]() ,
where the zodiacal light is
rather important at all helio-ecliptic longitudes. This is clearly visible
in the upper panel of Fig. 5, where we have over imposed the
telescope pointings on a contour plot of the zodiacal light V brightness,
obtained from the data published by Levasseur-Regourd & Dumont
(1980).
,
where the zodiacal light is
rather important at all helio-ecliptic longitudes. This is clearly visible
in the upper panel of Fig. 5, where we have over imposed the
telescope pointings on a contour plot of the zodiacal light V brightness,
obtained from the data published by Levasseur-Regourd & Dumont
(1980).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f5.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg60.gif) |
Figure 5:
Upper panel: distribution of telescope pointings
in helio-ecliptic coordinates. Over imposed is a contour plot of the
zodiacal light V brightness at the indicated levels expressed in sbu
(1 sbu = 10-9 erg s-1 cm-2 Å-1 sr-1). Original data
are from Levasseur-Regourd & Dumont (1980).
Lower panel: Zodiacal light V brightness profiles at four different
ecliptic latitudes expressed in sbu (left scale) and mag arcsec-2
(right scale). The brightness increase seen at
|
| Open with DEXTER | |
We note that the wavelength dependency of the zodiacal light contribution
is significant even within the optical range. In particular it reaches
its maximum contribution in the B passband,
where the ratio between zodiacal light and typical dark time sky
flux is always larger than 30%. On the opposite side we have the I
passband, where for
![]() 80
80![]() the
contribution is always smaller than 30% (see also O'Connell 1987).
Now, using the data from Levasseur-Regourd & Dumont (1980)
and the typical dark time sky brightness measured on Paranal, we can
estimate the sky brightness variations one expects on the basis of the
pure effect of variable zodiacal light contribution. As we have already
mentioned,
the largest variation is expected in the B band, where already
at
the
contribution is always smaller than 30% (see also O'Connell 1987).
Now, using the data from Levasseur-Regourd & Dumont (1980)
and the typical dark time sky brightness measured on Paranal, we can
estimate the sky brightness variations one expects on the basis of the
pure effect of variable zodiacal light contribution. As we have already
mentioned,
the largest variation is expected in the B band, where already
at
![]() 90
90![]() the sky becomes inherently brighter
by 0.4-0.5 mag as one goes from
the sky becomes inherently brighter
by 0.4-0.5 mag as one goes from ![]() 60
60![]() to
to ![]() 0
0![]() .
This variation decreases to
.
This variation decreases to ![]() 0.15 mag in the I passband.
0.15 mag in the I passband.
Due to the fact that the bulk of our data has been obtained at
![]() 30
30![]() ,
our dark time sky brightness estimates are
expected to be affected by systematic zodiacal light effects, which have
to be taken into account when comparing our results with those obtained
at high ecliptic latitudes for other astronomical sites (see
Sect. 5).
,
our dark time sky brightness estimates are
expected to be affected by systematic zodiacal light effects, which have
to be taken into account when comparing our results with those obtained
at high ecliptic latitudes for other astronomical sites (see
Sect. 5).
Another relevant aspect that one has to take into account when measuring the
night sky brightness is the contribution produced by scattered moon light.
Due to the scientific projects FORS1 was designed for, the large majority of
observations are carried out in dark time, either when the fractional lunar
illumination (FLI) is small or when the moon is below the horizon.
Nevertheless, according to the user's requirements, some observations are
performed when moon's contribution to the sky background is not negligible.
To evaluate the amount of moon light contamination at a given position on the
sky (which depends on several parameters, like target and moon elevation,
angular distance, FLI and extinction coefficient in the given passband) we
have used the model developed by Krisciunas & Schaefer (1991),
with the double aim of selecting those measurements which are not influenced
by moonlight and to test the model itself. We have forced
the lunar contribution to be zero when moon elevation is
![]() 18
18![]() and we have neglected any twilight effects.
On the one hand this has certainly the effect of overestimating the moon
contribution when -18
and we have neglected any twilight effects.
On the one hand this has certainly the effect of overestimating the moon
contribution when -18
![]() 0
0![]() ,
but on the other
hand it puts us on the safe side when selecting dark time data.
,
but on the other
hand it puts us on the safe side when selecting dark time data.
As expected, a large fraction of the observations were obtained practically with no moon: in more than 50% of the cases moon's addition is from 10-1 to 10-3 the typical dark sky brightness. Nevertheless, there is a substantial tail of observations where the contamination is relevant (200-400 sbu) and a few extreme cases were the moon is the dominating source (>600 sbu). This offers us the possibility of exploring both regimes.
We conclude the description of the statistical properties of our data set
by considering the solar activity during the relevant time interval.
As it has been first pointed out by Lord Rayleigh (1928), the
airglow emission is correlated with the sunspot number. As we have seen in
Sect. 1, this has been confirmed by a number of studies and
is now a widely accepted effect (see Walker 1988b and references therein).
As a matter of fact, all measurements presented in this work were taken
very close to the maximum of sunspot cycle No. 23, and thus we do not expect
to see any clear trend. This is shown in Fig. 6, where
we have plotted the monthly averaged Penticton-Ottawa solar flux at 2800 MHz
(Covington 1969)![]() .
We notice that the solar flux abruptly changed by a factor
.
We notice that the solar flux abruptly changed by a factor ![]() 2
between July and September 2001, leading to a second maximum which lasted
roughly two months at the end of year 2001. This might have some effect on
our data, which we will discuss later on.
2
between July and September 2001, leading to a second maximum which lasted
roughly two months at the end of year 2001. This might have some effect on
our data, which we will discuss later on.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{MS3223f6.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg66.gif) |
Figure 6: Penticton-Ottawa Solar flux at 2800 MHz (monthly average). The time range covered by the data presented in this paper is indicated by the thick line. The upper left insert traces the solar flux during the last six cycles. |
| Open with DEXTER | |
Due to the fact that our data set collects observations performed under
a wide range of conditions, in order to estimate the zenith sky brightness
during dark time it is necessary to apply some selection. For this
purpose we have adopted the following criteria: photometric conditions,
airmass ![]() 1.4, galactic latitude |b|> 10
1.4, galactic latitude |b|> 10![]() ,
time distance from
the closest twilight
,
time distance from
the closest twilight
![]() 1 hour and no moon (FLI = 0 or
1 hour and no moon (FLI = 0 or
![]() 18
18![]() ). Unfortunately,
as we have mentioned in Sect. 4.1, very few observations have
been carried out at
). Unfortunately,
as we have mentioned in Sect. 4.1, very few observations have
been carried out at ![]() 45
45![]() and hence we could not put
a very stringent constraint on the ecliptic latitude, contrary to what is
usually done (see for example Benn & Ellison 1998). To limit the
contribution of the zodiacal light, we could only restrict the range of
helio-ecliptic longitude (
and hence we could not put
a very stringent constraint on the ecliptic latitude, contrary to what is
usually done (see for example Benn & Ellison 1998). To limit the
contribution of the zodiacal light, we could only restrict the range of
helio-ecliptic longitude (
![]() 90
90![]() ).
The results one obtains from this selection are summarized in
Table 4 and Fig. 7, where we have plotted the
estimates of the sky brightness at zenith as a function of time.
Once one has accounted for the zodiacal light
bias (see below), the values are consistent with those
reported for other dark sites; in particular, they are very similar to
those presented by Mattila et al. (1996) for La Silla, which were
also obtained during a sunspot maximum (February 1978).
As pointed out by several authors, the dark time values show quite a strong
dispersion, which is typically of the order of 0.2 mag rms. Peak to peak
variations in the V band are as large as 0.8 mag, while this excursion
reaches 1.5 mag in the I band.
).
The results one obtains from this selection are summarized in
Table 4 and Fig. 7, where we have plotted the
estimates of the sky brightness at zenith as a function of time.
Once one has accounted for the zodiacal light
bias (see below), the values are consistent with those
reported for other dark sites; in particular, they are very similar to
those presented by Mattila et al. (1996) for La Silla, which were
also obtained during a sunspot maximum (February 1978).
As pointed out by several authors, the dark time values show quite a strong
dispersion, which is typically of the order of 0.2 mag rms. Peak to peak
variations in the V band are as large as 0.8 mag, while this excursion
reaches 1.5 mag in the I band.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f7.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg69.gif) |
Figure 7:
Zenith corrected sky brightness measured at Paranal
during dark time (thick dots) from April 1st, 2000 to September 30th, 2001.
The selection criteria are:
|b|> 10 |
| Open with DEXTER | |
| Filter | Sky Br. | Min | Max | N |
|
|
| U | 22.28 | 0.22 | 21.89 | 22.61 | 39 | 0.18 |
| B | 22.64 | 0.18 | 22.19 | 23.02 | 180 | 0.28 |
| V | 21.61 | 0.20 | 20.99 | 22.10 | 296 | 0.18 |
| R | 20.87 | 0.19 | 20.38 | 21.45 | 463 | 0.16 |
| I | 19.71 | 0.25 | 19.08 | 20.53 | 580 | 0.07 |
In Sect. 4.1 we have shown that the estimates presented in
Table 4 are surely influenced by zodiacal light effects of
low ecliptic latitudes. To give an idea of the amplitude of this
bias, in the last column of Table 4 we have reported the
correction
![]() one would have to apply to the average values
to compensate for this contribution. This has been computed as the average
correction derived from the data of Levasseur-Regourd & Dumont
(1980), assuming typical values for the dark time sky brightness:
as one can see,
one would have to apply to the average values
to compensate for this contribution. This has been computed as the average
correction derived from the data of Levasseur-Regourd & Dumont
(1980), assuming typical values for the dark time sky brightness:
as one can see,
![]() is as large as
is as large as ![]() 0.3 mag in the
B passband.
0.3 mag in the
B passband.
The sky brightness dependency on the ecliptic latitude is clearly displayed
in Fig. 8, where we have plotted the deviations from the
average sky brightness (cf. Table 4) for B, V and R
passbands, after applying the correction
![]() .
We have
excluded the I band because it is heavily dominated by airglow variations,
which completely mask any dependency from the position in the helio-ecliptic
coordinate system; the U data were also not included due to the small
sample. For comparison, in the same figure we have over imposed
the behaviour expected on the basis of Levasseur-Regourd & Dumont
(1980) data, which have been linearly interpolated to each of the
positions
.
We have
excluded the I band because it is heavily dominated by airglow variations,
which completely mask any dependency from the position in the helio-ecliptic
coordinate system; the U data were also not included due to the small
sample. For comparison, in the same figure we have over imposed
the behaviour expected on the basis of Levasseur-Regourd & Dumont
(1980) data, which have been linearly interpolated to each of the
positions
![]() in the data set.
As one can see, there is a rough agreement, the overall spread being quite
large. This is visible also in a similar plot produced by Benn &
Ellison (1998, their Fig. 10) and it is probably due to the night-to-night
fluctuations in the airglow contribution.
in the data set.
As one can see, there is a rough agreement, the overall spread being quite
large. This is visible also in a similar plot produced by Benn &
Ellison (1998, their Fig. 10) and it is probably due to the night-to-night
fluctuations in the airglow contribution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f8.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg72.gif) |
Figure 8: B, V and R dark time sky brightness variations as a function of ecliptic latitude. The solid lines trace the behaviour expected from Levasseur-Regourd & Dumont (1980) data for the different passbands. |
| Open with DEXTER | |
In the literature one can find several and discordant results about the
sky brightness variations as a function of the time distance from
astronomical twilight. Walker (1988b) first pointed out that the
sky at zenith gets darker by ![]() 0.4 mag arcsec-2 during the
first six hours after the end of twilight. Pilachowski et al. (1989)
found dramatic short time scale variations, while the steady
variations were attributed to airmass effects only (see their Fig. 2). This
explanation looks indeed reasonable, since the observed sky
brightening is in agreement with the predictions of Garstang
(1989).
Krisciunas (1990, his Fig. 6) found that his data obtained in the
V passband showed a decrease of
0.4 mag arcsec-2 during the
first six hours after the end of twilight. Pilachowski et al. (1989)
found dramatic short time scale variations, while the steady
variations were attributed to airmass effects only (see their Fig. 2). This
explanation looks indeed reasonable, since the observed sky
brightening is in agreement with the predictions of Garstang
(1989).
Krisciunas (1990, his Fig. 6) found that his data obtained in the
V passband showed a decrease of ![]() 0.3 mag arcsec-2 in the
first six hours after the end of twilight, but he also remarked that this
effect was not clearly seen in B.
Due to the high artificial light pollution, Lockwood et al. (1990) tend to attribute the nightly sky brightness decline they observe at the Lowell Observatory, to progressive reduction of
commercial activity.
0.3 mag arcsec-2 in the
first six hours after the end of twilight, but he also remarked that this
effect was not clearly seen in B.
Due to the high artificial light pollution, Lockwood et al. (1990) tend to attribute the nightly sky brightness decline they observe at the Lowell Observatory, to progressive reduction of
commercial activity.
Walker's findings were questioned by Leinert et al. (1995) and Mattila et al. (1996), who state that no indications for systematic every-night behaviour of a decreasing sky brightness after the end of twilight were shown by their observations. Krisciunas (1997) notes that, on average, the zenith sky brightness over Mauna Kea shows a not very convincing sky brightness change of 0.03 mag hour-1. On the other hand he also reports cases where the darkening rate was as large as 0.24 mag hour-1 and discusses the possibility of a reverse Walker effect taking place during a few hours before the beginning of morning twilight.
Leinert et al. (1998) touch this topic in their extensive review, pointing out that this is an often observed effect due to a decreasing release rate of the energy stored in the atmospheric layers during day time. Finally, Benn & Ellison (1998) do not find any signature of steady sky brightness variation depending on the time distance from twilights at La Palma, and suggest that the effect observed by Walker is due to the variable contribution of the zodiacal light, a hypothesis already discussed by Garstang (1997). A further revision of Walker's findings is presented here in Appendix D, where we show that the effect is significantly milder than it was thought and probably influenced by a small number of well sampled nights.
We have performed an analogous analysis on our
data set, using only the measurements obtained during dark time and
correcting for differential zodiacal light contribution. Since the time
range covered by our observations is relatively small with respect to
the solar cycle, we do not expect the solar activity to play a relevant
role, and hence we reckon it is reasonable not to normalise the measured
sky brightness to some reference time. This operation would be anyway very
difficult, due to the vast amount of data and the lack of long time
series. The results are presented in Fig. 9, where we
have plotted the sky brightness vs. time from evening twilight,
![]() ,
for B, V, R and I passbands. Our data do not support the exponential drop seen by
Walker (1988b) during the first 4 hours and confirm the findings
by Leinert et al. (1995), Mattila et al. (1996) and
Benn & Ellison (1998). This is particularly true for V and R data,
while in B and especially in I one might argue that some evidence of
a rough trend is visible. As a matter of fact, a blind linear least squares
fit in the range 0
,
for B, V, R and I passbands. Our data do not support the exponential drop seen by
Walker (1988b) during the first 4 hours and confirm the findings
by Leinert et al. (1995), Mattila et al. (1996) and
Benn & Ellison (1998). This is particularly true for V and R data,
while in B and especially in I one might argue that some evidence of
a rough trend is visible. As a matter of fact, a blind linear least squares
fit in the range 0
![]() 6 gives an average slope
of 0.04
6 gives an average slope
of 0.04 ![]() 0.01 and 0.03
0.01 and 0.03 ![]() 0.01 mag hour-1 for the two passbands
respectively. Both values are a factor of two smaller than those
found by Walker (1988b) but are consistent, within the quoted
errors, with the values we found revising his original data
(see Appendix D).
However, the fact that no average steady decline is seen in V and R casts
some doubt on the statistical significance of the results one gets from
B and I data.
This does not mean that on some nights very strong declines can be seen, as
already pointed out by Krisciunas (1997). Our data set includes
several such examples, but probably the most interesting is the one which is
shown in Fig. 10, where we have plotted the data collected
on five consecutive nights (2000 April 3-7). As one can see, the I data
(upper panel) show a clear common trend, even though segments with different
slopes are present and the behaviour shown towards the end of the night during
2000 April 6 is opposite to that of 2000 April 5. This trend becomes less
clear in the R passband (middle panel) and it is definitely not visible in
V (lower panel), where the sky brightness remains practically constant for
about 6 hours. Unfortunately, no B data are available during these nights.
0.01 mag hour-1 for the two passbands
respectively. Both values are a factor of two smaller than those
found by Walker (1988b) but are consistent, within the quoted
errors, with the values we found revising his original data
(see Appendix D).
However, the fact that no average steady decline is seen in V and R casts
some doubt on the statistical significance of the results one gets from
B and I data.
This does not mean that on some nights very strong declines can be seen, as
already pointed out by Krisciunas (1997). Our data set includes
several such examples, but probably the most interesting is the one which is
shown in Fig. 10, where we have plotted the data collected
on five consecutive nights (2000 April 3-7). As one can see, the I data
(upper panel) show a clear common trend, even though segments with different
slopes are present and the behaviour shown towards the end of the night during
2000 April 6 is opposite to that of 2000 April 5. This trend becomes less
clear in the R passband (middle panel) and it is definitely not visible in
V (lower panel), where the sky brightness remains practically constant for
about 6 hours. Unfortunately, no B data are available during these nights.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3223f9.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg75.gif) |
Figure 9: Dark time Paranal night sky brightness, corrected for zodiacal light contribution, as a function of time distance from evening twilight. The vertical dotted lines indicate the shortest and longest night (7.4 and 10.7 hours respectively, astronomical twilight to twilight), while the dashed horizontal line is placed at the average value in each passband. |
| Open with DEXTER | |
A couple of counter-examples are shown in Fig. 11: the
upper and lower panels show two well sampled time series obtained on the
same sky patch, which show that during those nights the sky brightness
was roughly constant during the phase where the Walker effect is expected
to be most efficiently at work. Instead of a steady decline, clear and smooth
sinusoidal fluctuations with maximum amplitudes of ![]() 0.1 mag and time
scales of the order of 0.5 hours are well visible. Finally, to show that
even mixed behaviours can take place, in the central panel we have presented
the R data collected on 23-02-2001, when a number of different sky patches
was observed. During that night, the sky brightness had a peak-to-peak
fluctuation of
0.1 mag and time
scales of the order of 0.5 hours are well visible. Finally, to show that
even mixed behaviours can take place, in the central panel we have presented
the R data collected on 23-02-2001, when a number of different sky patches
was observed. During that night, the sky brightness had a peak-to-peak
fluctuation of ![]() 0.7 mag and showed a steady increase for at least
4 hours.
0.7 mag and showed a steady increase for at least
4 hours.
To conclude, we must say that we tend to agree with Leinert et al. (1995) that the behaviour shown during single nights covers a wide variety of cases and that there is no clear average trend. We also add that mild time-dependent effects cannot be ruled out; they are probably masked by the much wider night-to-night fluctuations and possibly by the patchy nature of the night sky even during the same night.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3223f10.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg76.gif) |
Figure 10: Time sequences collected on April 2-7, 2000. The data have been corrected for airmass and differential zodiacal light contribution. The vertical dotted line is placed at the beginning of morning astronomical twilight. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3223f11.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg77.gif) |
Figure 11: Time sequences collected on 19-12-2000 (I), 23-02-2001 (R) and 16-07-2001 (I). The data have been corrected for airmass and differential zodiacal light contribution. The vertical dotted line is placed at the beginning of morning astronomical twilight. |
| Open with DEXTER | |
As we have mentioned in Sect. 4.2, some data have been collected when the moon contribution to the sky brightness is conspicuous and this offers us the possibility of directly measuring its effect and comparing it with the model by Krisciunas & Schaefer (1991) which, to our knowledge, is the only one available in the literature.
To estimate the fraction of sky brightness generated by scattered moon
light, we have subtracted to the observed fluxes the average values
reported in Table 4 for each passband. The results are presented
in the lower panel of Fig. 12, where we have plotted only
those data for which the observed value was larger than the dark time one.
As expected, the largest deviations are seen in B, where the sky brightness
can increase by about 3 mag at 10 days after new moon, while in I, at
roughly the same moon age, this deviation just reaches ![]() 1.2 mag. It is
interesting to note that most exposure time calculators for modern instruments
make use of the function published by Walker (1987) to compute
the expected sky brightness as a function of moon age. As already noticed
by Krisciunas (1990), this gives rather optimistic estimates, real
data being most of the time noticeably brighter. This is clearly visible in
Fig. 12, where we have overplotted Walker's function
for the V passband to our data: already at 6 days past new moon the
observed V data (open squares) show maximum deviations of the order of 1 mag. These results are fully compatible with those presented by Krisciunas
(1990) in his Fig. 8.
1.2 mag. It is
interesting to note that most exposure time calculators for modern instruments
make use of the function published by Walker (1987) to compute
the expected sky brightness as a function of moon age. As already noticed
by Krisciunas (1990), this gives rather optimistic estimates, real
data being most of the time noticeably brighter. This is clearly visible in
Fig. 12, where we have overplotted Walker's function
for the V passband to our data: already at 6 days past new moon the
observed V data (open squares) show maximum deviations of the order of 1 mag. These results are fully compatible with those presented by Krisciunas
(1990) in his Fig. 8.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3223f12.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg78.gif) |
Figure 12: Lower panel: observed sky brightness variation as a function of moon age for B, V, R and I. The solid line traces the data published by Walker (1987) for the V passband while the upper scale shows the fractional lunar illumination. Upper panel: comparison between the observed and predicted moon contribution (Krisciunas & Schaefer 1991). Plotted are only those data points for which the global brightness is larger than the typical dark time brightness. |
| Open with DEXTER | |
Another weak point of Walker's function is that it has one input parameter only, namely the moon phase, and this is clearly not enough to predict with sufficient accuracy the sky brightness. This, in fact, depends on a number of parameters, some of which, of course, are known only when the time the target is going to be observed is known. In this respect, the model by Krisciunas & Schaefer (1991) is much more promising, since it takes into account all relevant astronomical circumstances. The model accuracy was tested by the authors themselves, who reported rms deviations as large as 23% in a brightness range which spans over 20 times the typical value observed during dark time.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3223f13.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg79.gif) |
Figure 13: Lower panel: nightly average sky brightness in the R passband vs. solar density flux. The filled circles represent data taken at MJD > 52114, while the solid line indicates a linear least squares fit to all data. Upper panel: Penticton-Ottawa solar flux at 2800 MHz during the time interval discussed in this paper. The open circles indicate the values which correspond to the data presented in the lower panel and the dotted line is placed at the median value for the solar density flux. |
| Open with DEXTER | |
In the upper panel of Fig. 12 we have compared our results
with the model predictions, including B,V,R and I data. We emphasise
that we have used average values for the extinction coefficients and dark
time sky brightness and this certainly has some impact on the computed
values. On the other hand, this is the typical configuration
under which the procedure would be implemented in an exposure time
calculator, and hence it gives a realistic evaluation of the model
practical accuracy. Figure 12 shows that, even if deviations
as large as 0.4 mag are detected, the model gives a reasonable reproduction
of the data in the brightness range covered by our observations. This is
actually less than half with respect to the one encompassed by the data
shown in Fig. 3 of Krisciunas & Schaefer (1991), which reach
![]() 8300 sbu in the V band.
8300 sbu in the V band.
| Site | Year |
|
U | B | V | R | I | Reference |
| MJy | mag arcsec-2 | |||||||
| La Silla | 1978 | 1.5 | - | 22.8 | 21.7 | 20.8 | 19.5 | Mattila et al. (1996) |
| Kitt Peak | 1987 | 0.9 | - | 22.9 | 21.9 | - | - | Pilachowski et al. (1989) |
| Cerro Tololo | 1987-8 | 0.9 | 22.0 | 22.7 | 21.8 | 20.9 | 19.9 | Walker (1987, 1988a) |
| Calar Alto | 1990 | 2.0 | 22.2 | 22.6 | 21.5 | 20.6 | 18.7 | Leinert et al. (1995) |
| La Palma | 1994-6 | 0.8 | 22.0 | 22.7 | 21.9 | 21.0 | 20.0 | Benn & Ellison (1998) |
| Mauna Kea | 1995-6 | 0.8 | - | 22.8 | 21.9 | - | - | Krisciunas (1997) |
| Paranal | 2000-1 | 1.8 | 22.3 | 22.6 | 21.6 | 20.9 | 19.7 | this work |
As we have mentioned in Sect. 4.3, during the time covered
by the data presented here, the solar activity had probably reached its
maximum. To be more precise, since the current solar cycle (No. 23) has
a double peak structure (see Fig. 6), our measurements cover
the descent from the first maximum and the abrupt increase to the second
maximum. Mainly due to the latter transition, the solar density flux
at 10.7 cm in our data set ranges from 1.2 MJy to 2.4 MJy, the median value
being 1.8 MJy.
Even though this is almost half of the full range expected on a typical
complete 11 years solar cycle (0.8-2.5 MJy), a clear
variation is seen in the same solar density flux range from similar analysis
performed by other authors (see for example Mattila et al. 1996, their
Fig. 6). In Fig. 13 we show the case of the R passband, where
we have plotted the nightly average sky brightness vs. the solar density flux
measured during the day immediately preceeding the observations. A linear
least squares fit to the data (solid line) gives a slope of
0.14 ![]() 0.01 mag arcsec-2 MJy-1, which turns
into a variation of 0.24
0.01 mag arcsec-2 MJy-1, which turns
into a variation of 0.24 ![]() 0.11 mag arcsec-2 during a full solar
cycle. This value is a factor two smaller than what has been reported
for B, V (Walker 1988b; Krisciunas 1990) and uvgyr
(Leinert et al. 1995; Mattila et al. 1996) for yearly averages and it is
consistent with a null variation at the 2 sigma level. Moreover,
since the correlation factor computed for the data in Fig. 13
is only 0.19, we think there is no clear indication for a real dependency.
0.11 mag arcsec-2 during a full solar
cycle. This value is a factor two smaller than what has been reported
for B, V (Walker 1988b; Krisciunas 1990) and uvgyr
(Leinert et al. 1995; Mattila et al. 1996) for yearly averages and it is
consistent with a null variation at the 2 sigma level. Moreover,
since the correlation factor computed for the data in Fig. 13
is only 0.19, we think there is no clear indication for a real dependency.
This impression is confirmed by the fact that a similar analysis for
the B and V passbands gives an extrapolated variation of 0.08 ![]() 0.13
and 0.07
0.13
and 0.07 ![]() 0.11 mag arcsec-2 respectively. These numbers, which
are consistent with zero, and the low correlation coefficients
(0.08 and 0.11 respectively) seem to indicate no short-term dependency
from the 10.7 cm solar flux. Similar values
are found for the I passband (
0.11 mag arcsec-2 respectively. These numbers, which
are consistent with zero, and the low correlation coefficients
(0.08 and 0.11 respectively) seem to indicate no short-term dependency
from the 10.7 cm solar flux. Similar values
are found for the I passband (![]() 0.22
0.22 ![]() 0.15 mag arcsec-2).
These results agree with the findings by Leinert et al. (1995)
and Mattila et al. (1996) and the early work of
Rosenberg & Zimmermann (1967), who have shown that the [OI]5577 Å line intensity correlates with the 2800 MHz solar flux much more
strongly using the monthly averages than the nightly averages.
For all these reasons, we agree with Mattila et al. (1996) in saying
that no firm prediction on the night sky brightness can be made on the basis
of the solar flux measured during the day preceeding the observations,
as it was initially suggested by Walker (1988b).
A possible physical explanation for this effect is that there is some inertia
in the energy release from the layers ionised by the solar UV radiation, such
that what counts is the integral over some typical time scale rather than
the instantaneous energy input.
0.15 mag arcsec-2).
These results agree with the findings by Leinert et al. (1995)
and Mattila et al. (1996) and the early work of
Rosenberg & Zimmermann (1967), who have shown that the [OI]5577 Å line intensity correlates with the 2800 MHz solar flux much more
strongly using the monthly averages than the nightly averages.
For all these reasons, we agree with Mattila et al. (1996) in saying
that no firm prediction on the night sky brightness can be made on the basis
of the solar flux measured during the day preceeding the observations,
as it was initially suggested by Walker (1988b).
A possible physical explanation for this effect is that there is some inertia
in the energy release from the layers ionised by the solar UV radiation, such
that what counts is the integral over some typical time scale rather than
the instantaneous energy input.
Besides being the first systematic campaign of night sky brightness
measurements at Cerro Paranal, the survey we have presented here has many
properties that make it rather unique. First of all, the fact that it is
completely automatic ensures that each single frame which passes through
the quality checks contributes to build a continously growing sample. Furthermore,
since the data are produced by a very large telescope, the measurements
accuracy is quite high when compared to that generally achieved
in this kind of study, which most of the time make use of small telescopes.
Another important fact, related to both the large collecting area and the
use of a CCD detector, is that the usual problem of faint
unresolved stars is practically absent. In fact, with small telescopes,
it is very difficult to avoid the inclusion of stars fainter than V= 13
in the beam of the photoelectric photometer (see for example Walker 1988b).
The contribution of such stars is 39.1 S10(V) (Roach & Gordon 1973,
Table 2-I) which corresponds to about 13% of the global sky brightness. Now,
with the standard configuration and a seeing of 1
![]() ,
during dark time FORS1 can reach a 5
,
during dark time FORS1 can reach a 5![]() peak limiting magnitude
peak limiting magnitude
![]() 23.3 in a 60 s exposure for unresolved objects. As the
simulations show (see Patat 2003), the algorithm we have adopted to
estimate the sky background is practically undisturbed by the presence of
such stars, unless their number is very large, a case which would be
rejected anyway by the
23.3 in a 60 s exposure for unresolved objects. As the
simulations show (see Patat 2003), the algorithm we have adopted to
estimate the sky background is practically undisturbed by the presence of
such stars, unless their number is very large, a case which would be
rejected anyway by the ![]() -test (Patat 2003).
Now, since the typical contribution of stars with
-test (Patat 2003).
Now, since the typical contribution of stars with ![]() 20 is 3.2 S10(V)(Roach & Gordon 1973), we can conclude that the effect of
faint unresolved stars on our measurements is less than 1%.
20 is 3.2 S10(V)(Roach & Gordon 1973), we can conclude that the effect of
faint unresolved stars on our measurements is less than 1%.
Another distinguishing feature is the time coverage. As reported by Benn & Ellison (1998), the large majority of published sky brightness measurements were carried out during a limited number of nights (see their Table 1). The only remarkable exception is represented by their own work, which made use of 427 CCD images collected on 63 nights in ten years. Nevertheless, this has to be compared with our survey which produced about 3900 measurements during the first 18 months of steady operation. This high time frequency allows one to carry out a detailed analysis of time dependent effects, as we have shown in Sect. 6 and to get statistically robust estimates of the typical dark time zenith sky brightness.
The values we have obtained for Paranal are compared to
those of other dark astronomical sites in Table 5.
The first thing one notices is that the values for Cerro Paranal are very
similar to those reported for La Silla, which were also obtained during
a maximum of solar activity. They are also not very different from those
of Calar Alto, obtained in a similar solar cycle phase, even though
Paranal and La Silla are clearly darker in R and definitely in I.
All other sites presented in Table 5 have data which were
obtained during solar minima and are therefore expected to show systematically
lower sky brightness values. This is indeed the case. For example, the
V values measured at Paranal are about 0.3 mag brighter then those
obtained at other sites at minimum solar activity (Kitt Peak, Cerro
Tololo, La Palma and Mauna Kea). The same behaviour, even though somewhat
less pronounced, is seen in B and I, while it is much less obvious in R.
Finally, the U data show an inverse trend, in the sense that at those
wavelengths the sky appears to be brighter at solar minima. Interestingly,
a plot similar to that of Fig. 13 also gives
a negative slope, which turns into a variation
![]() 0.7
0.7 ![]() 0.5 mag arcsec-2 during a full solar cycle. Due to the rather large error
and the small number of nights (11), we think that no firm conclusion can be
drawn about a possible systematic effect, but we notice that a similar behaviour is
found by Leinert et al. (1995) for the u passband (see their
Fig. 6). Since the airglow in U is dominated by the O2 Herzberg bands
0.5 mag arcsec-2 during a full solar cycle. Due to the rather large error
and the small number of nights (11), we think that no firm conclusion can be
drawn about a possible systematic effect, but we notice that a similar behaviour is
found by Leinert et al. (1995) for the u passband (see their
Fig. 6). Since the airglow in U is dominated by the O2 Herzberg bands
![]() (Broadfoot & Kendall 1968), the fact that their
intensity seems to decrease with an increasing ionising solar flux could
probably give some information on the physical state of the emitting layers,
where molecular oxygen is confined.
(Broadfoot & Kendall 1968), the fact that their
intensity seems to decrease with an increasing ionising solar flux could
probably give some information on the physical state of the emitting layers,
where molecular oxygen is confined.
At any rate, the BVRI Paranal sky brightness will probably decrease in the next 5-6 years, to reach its natural minimum around 2007. The expected darkening is of the order of 0.4-0.5 mag arcsec-2 (Walker 1988b), but the direct measurements will give the exact values for this particular site. In the next years this survey will provide an unprecedented mapping of the dependency from solar activity. So far, in fact, this correlation has been investigated with sparse data, affected by a rather high spread due to the night-to-night variations of the airglow (see for instance Fig. 4 by Krisciunas 1990), which tend to mask any other effect and make any conclusion rather uncertain.
As already pointed out by several authors, the night sky can vary
significantly over different time scales, following physical processes that
are not completely understood. As we have shown in the previous section,
even the daily variations in the solar ionising radiation are not sufficient
to account for the observed night-to-night fluctuations. Moreover, the
observed scatter in the dark time sky brightness (see Sect. 5)
is certainly not produced by the measurement accuracy and can be as large as
0.25 mag (rms) in the I passband; since the observed distribution is
practically Gaussian (see Fig. 7), this means that the I sky
brightness can range over ![]() 1.4 mag, even after removing the effects of
airmass and zodiacal light contribution. This unpredictable variation has
the unpleasant effect of causing maximum signal-to-noise changes of about a
factor of 2.
1.4 mag, even after removing the effects of
airmass and zodiacal light contribution. This unpredictable variation has
the unpleasant effect of causing maximum signal-to-noise changes of about a
factor of 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f14.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg86.gif) |
Figure 14:
V, R and I (from top to bottom) dark time
sky brightness measured at Paranal from April 2000 to September 2001.
For each passband the average value (dashed line) and the |
| Open with DEXTER | |
Besides these short time scale fluctuations that we have discussed in
Sect. 6 and the long term variation due to the solar cycle,
one can reasonably expect some effects on intermediate time scales. With this
respect we have computed the sky brightness values averaged over three months
intervals, centered on solstices and equinoxes. The results for V, R and
I are plotted in Fig. 14, where we have used all the
available data obtained at Paranal during dark time, with
![]() 0.
This figure shows that there is no convincing
evidence for any seasonal effect, especially in the I passband, where all
three-monthly
values are fully consistent with the global average (thick dashed line). The
only marginal detection of a deviation from the overall trend is that seen in
R in correspondence of the austral summer of year 2000, when the average
sky brightness turns out to be
0.
This figure shows that there is no convincing
evidence for any seasonal effect, especially in the I passband, where all
three-monthly
values are fully consistent with the global average (thick dashed line). The
only marginal detection of a deviation from the overall trend is that seen in
R in correspondence of the austral summer of year 2000, when the average
sky brightness turns out to be ![]() 1.3
1.3![]() fainter than the global
average value. Even though a decrease of about 0.1 mag is indeed expected in
the R passband as a consequence of the NaI D flux variation (see Roach &
Gordon 1973 and the discussion below), we are not completely sure this is
the real cause of the observed effect, both because of the low statistical
significance and the fact that a similar, even though less pronounced drop,
is seen at the same epoch in the V band, where the NaI D line contribution
is negligible (see Fig. 1).
fainter than the global
average value. Even though a decrease of about 0.1 mag is indeed expected in
the R passband as a consequence of the NaI D flux variation (see Roach &
Gordon 1973 and the discussion below), we are not completely sure this is
the real cause of the observed effect, both because of the low statistical
significance and the fact that a similar, even though less pronounced drop,
is seen at the same epoch in the V band, where the NaI D line contribution
is negligible (see Fig. 1).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f15.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg88.gif) |
Figure 15:
Evolution of the night sky spectrum on
February 25, 2001 in the wavelength range 5500-6500 Å. The original
1800 s spectra were obtained with FORS1, using the standard resolution
collimator and a long slit 1
|
| Open with DEXTER | |
To illustrate how complex the night sky variations can be, we present a
sequence of four spectra taken at Paranal during a moonless night in
Fig. 15, starting more than two hours after evening
twilight with an airmass ranging from 1.4 to 2.0. For the sake of simplicity
we concentrate on the spectral region 5500-6500 Å, right at the intersection
between V and R passbands, which contains the brightest optical emission
lines and the so called pseudo-continuum (see Sect. 1). Due to
the increasing airmass, the overall sky brightness is expected to grow
according to Eq. (C.3), which for V and R gives a variation of
about 0.2 mag. These values are in rough agreement with those
one gets measuring the continuum variation at 5500 Å (0.13 mag) and
6400 Å (0.18 mag). Interestingly, this is not the case for the
synthetic V and R magnitudes derived from the same spectra, which decrease
by 0.32 and 0.51 mag respectively, i.e. much more than expected, specially
in the R band. This already tells us that the continuum and the emission lines
must behave in a different manner.
In fact, the flux carried by the [OI]5577 Å line changes by a factor 1.9
from the first to the last spectrum, whereas the adjacent continuum
grows only by a factor 1.1. For the NaI D lines, these two numbers are 1.4
and 1.2, still indicating a dichotomy between the pseudo-continuum and the
emission lines. But the most striking behaviour is that displayed by the
[OI]6300, 6364 Å doublet: the integrated flux changes by a factor 5.2 in about two hours and can be easily identified
as the responsible for the brightening observed in the R passband.
This is easily visible in Fig. 15, where the [OI]6300 Å
component surpasses the [OI]5577 Å in the transition from the first to
the second spectrum and keeps growing in intensity in the subsequent two
spectra. The existence of these abrupt changes is known since the
pioneering work by Barbier (1957), who has shown that
[OI]6300, 6364 Å
can undergo strong brightness enhancements over an hour or two on two
active regions about 20![]() on either side of the geomagnetic equator,
which roughly corresponds to tropical sites. With Cerro Paranal included in
one of these active areas, such events are not unexpected. A possible physical
explanation for this effect is described by Ingham (1972), and
involves the release of charged particles at the conjugate point of the
ionosphere, which stream along the lines of force of the terrestrial magnetic
field. We notice that in our example, the first spectrum was taken about two
hours before local midnight, at about one month before the end of austral
summer. This is in contrast with Ingham's explanation, which implies that
this phenomenon should take place in local winter, since in local summer the
conjugate point, which for Paranal lies in the northern hemisphere, sees the
sun later and not before, as it is the case during local winter.
on either side of the geomagnetic equator,
which roughly corresponds to tropical sites. With Cerro Paranal included in
one of these active areas, such events are not unexpected. A possible physical
explanation for this effect is described by Ingham (1972), and
involves the release of charged particles at the conjugate point of the
ionosphere, which stream along the lines of force of the terrestrial magnetic
field. We notice that in our example, the first spectrum was taken about two
hours before local midnight, at about one month before the end of austral
summer. This is in contrast with Ingham's explanation, which implies that
this phenomenon should take place in local winter, since in local summer the
conjugate point, which for Paranal lies in the northern hemisphere, sees the
sun later and not before, as it is the case during local winter.
Irrespective of the underlying physical mechanism, the [OI]6300, 6364 Å
line intensity![]() changed from 255 R to 1330 R; the fact that the initial value is
definitely higher than that expected at these geomagnetic latitudes (<50 R,
Roach & Gordon 1973, Figs. 4-12) seems to indicate that the line brightening
had started before our first observation. On the other hand, the intensity of
the [OI]5577 Å line in the first spectrum is 220 R, i.e. well in agreement
with the typical value (250 R, Schubert & Walterscheid 2000).
changed from 255 R to 1330 R; the fact that the initial value is
definitely higher than that expected at these geomagnetic latitudes (<50 R,
Roach & Gordon 1973, Figs. 4-12) seems to indicate that the line brightening
had started before our first observation. On the other hand, the intensity of
the [OI]5577 Å line in the first spectrum is 220 R, i.e. well in agreement
with the typical value (250 R, Schubert & Walterscheid 2000).
The case of NaI D lines is slightly different, since these features follow a strong seasonal variation which makes them brighter in winter and fainter in summer, the intensity range being 30-200 R (Schubert & Walterscheid 2000). This fluctuation is expected to produce a seasonal variation with an amplitude of about 0.1 mag in the R passband, while in V the effect is negligible. Actually, the minimum intensity of this feature can change from site to site, according to the amount of light pollution. In fact, most of the radiation produced by low-pressure sodium lamps is released through this transition. For example, Benn & Ellison (1998) report for La Palma an estimated artificial contribution to the sodium D lines of about 70 R. In our first spectrum, the measured intensity is 73 R, a value which, together with the epoch when it was obtained (end of summer) and the relatively large airmass (X= 1.5), indicates a very small contribution from artificial illumination. However, a firmer limit can be set analysing a large sample of low resolution spectra taken around midsummer, a task which is beyond the purpose of this paper.
To search for other possible signs of light pollution, we have examined
the wavelength range 3500-5500 Å of the last spectrum presented in
Fig. 15, which was obtained at a zenith distance of about
60![]() and at an azimuth of 313
and at an azimuth of 313![]() .
A number of Hg and Na lines produced by street lamps, which are clearly
detected at polluted sites, falls in this spectral region.
As expected, there is no clear trace of such features in the examined
spectrum; in particular, the strongest among these lines, HgI 4358 Å, is
definitely absent. This appears clearly in Fig. 16, where
we have plotted the relevant spectral region and the expected positions
for the brightest Hg and Na lines (Osterbrock & Martel 1992). In the same
figure we have also marked the positions of O2 and OH main features.
A comparison with the spectra presented by Broadfoot & Kendall
(1968) again confirms the absence of the HgI lines and shows that
almost all features can be confidently identified with natural transitions of
molecular oxygen and hydroxyl. There are probably two exceptions only, which
happen to be observed very close to the expected positions for NaI 4978,
4983 Å and NaI 5149, 5163 Å, lines typically produced by high
pressure sodium lamps (Benn & Ellison 1998). They are very weak,
with an intensity smaller than 2 R, and their contribution to the broad
band sky brightness is negligible. Nevertheless, if real, they
could indicate the possible presence of some artificial component in the NaI D lines, which are typically much brighter. This can be verified with
the analysis of a high resolution spectrum. If the contamination is really
present, this should show up with the broad components which are a clear
signature of high pressure sodium lamps. The inspection of a low airmass,
high resolution (R= 43 000) and high signal-to-noise UVES spectrum of
Paranal's night sky (Hanuschik et al. 2003, in preparation) has shown no
traces of neither such broad components nor of other NaI and HgI lines.
For this purpose, suitable UVES observations at critical directions
(Antofagasta, Yumbes mining plant) and high airmass periodically executed
during technical nights, would probably allow one to detect much weaker
traces of light pollution than any broad band photometric survey. But,
in conclusion, there is no indication for any azimuth dependency in our
dark time UBVRI measurements.
.
A number of Hg and Na lines produced by street lamps, which are clearly
detected at polluted sites, falls in this spectral region.
As expected, there is no clear trace of such features in the examined
spectrum; in particular, the strongest among these lines, HgI 4358 Å, is
definitely absent. This appears clearly in Fig. 16, where
we have plotted the relevant spectral region and the expected positions
for the brightest Hg and Na lines (Osterbrock & Martel 1992). In the same
figure we have also marked the positions of O2 and OH main features.
A comparison with the spectra presented by Broadfoot & Kendall
(1968) again confirms the absence of the HgI lines and shows that
almost all features can be confidently identified with natural transitions of
molecular oxygen and hydroxyl. There are probably two exceptions only, which
happen to be observed very close to the expected positions for NaI 4978,
4983 Å and NaI 5149, 5163 Å, lines typically produced by high
pressure sodium lamps (Benn & Ellison 1998). They are very weak,
with an intensity smaller than 2 R, and their contribution to the broad
band sky brightness is negligible. Nevertheless, if real, they
could indicate the possible presence of some artificial component in the NaI D lines, which are typically much brighter. This can be verified with
the analysis of a high resolution spectrum. If the contamination is really
present, this should show up with the broad components which are a clear
signature of high pressure sodium lamps. The inspection of a low airmass,
high resolution (R= 43 000) and high signal-to-noise UVES spectrum of
Paranal's night sky (Hanuschik et al. 2003, in preparation) has shown no
traces of neither such broad components nor of other NaI and HgI lines.
For this purpose, suitable UVES observations at critical directions
(Antofagasta, Yumbes mining plant) and high airmass periodically executed
during technical nights, would probably allow one to detect much weaker
traces of light pollution than any broad band photometric survey. But,
in conclusion, there is no indication for any azimuth dependency in our
dark time UBVRI measurements.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f16.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg89.gif) |
Figure 16: Night sky spectrum obtained at Paranal on February 25, 2002 at 04:53 UT (see Fig. 15). Marked are the expected positions for the most common lines produced by artificial scattered light (upper ticks) and natural atmospheric features (lower ticks). The dotted line traces part of the spectrum taken during the same night at 02:39 UT. |
| Open with DEXTER | |
There are finally two interesting features shown in Fig. 16
which deserve a short discussion. The first is the presence of CaII H&K
absorption lines, which are clearly visible also in the spectra presented
by Broadfoot & Kendall (1968) and are the probable result
of sunlight scattered by interplanetary dust (Ingham 1962). This is not
surprising, since the spectrum of Fig. 16 was taken at
![]() 3$.^$5 and
3$.^$5 and
![]() 139$.^$8, i.e. in
a region were the contribution from the zodiacal light is significant
(see Fig. 5).
The other interesting aspect concerns the emission at about 5200 Å.
This unresolved feature, identified as NI, is extremely weak in the spectra of
Broadfoot & Kendall (1968), in agreement with its typical
intensity (1 R, Roach & Gordon 1973). On the contrary, in our first
spectrum (dotted line in Fig. 16) it is very clearly detected
at an intensity of 7.5 R and steadily grows until it reaches 32 R in the
last spectrum, becoming the brightest feature in this wavelength range.
This line, which is actually a blend of several very close NI transitions, is
commonly seen in the Aurora spectrum with intensities of 0.1-2 kR (Schubert & Walterscheid 2000) and it is supposed to originate in
a layer at 258 km. The fact that its observed growth (by a factor 4.3) follows
closely the one we have discussed for [OI]6300, 6364 Å, suggests that the
two regions probably undergo the same micro-auroral processes.
139$.^$8, i.e. in
a region were the contribution from the zodiacal light is significant
(see Fig. 5).
The other interesting aspect concerns the emission at about 5200 Å.
This unresolved feature, identified as NI, is extremely weak in the spectra of
Broadfoot & Kendall (1968), in agreement with its typical
intensity (1 R, Roach & Gordon 1973). On the contrary, in our first
spectrum (dotted line in Fig. 16) it is very clearly detected
at an intensity of 7.5 R and steadily grows until it reaches 32 R in the
last spectrum, becoming the brightest feature in this wavelength range.
This line, which is actually a blend of several very close NI transitions, is
commonly seen in the Aurora spectrum with intensities of 0.1-2 kR (Schubert & Walterscheid 2000) and it is supposed to originate in
a layer at 258 km. The fact that its observed growth (by a factor 4.3) follows
closely the one we have discussed for [OI]6300, 6364 Å, suggests that the
two regions probably undergo the same micro-auroral processes.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS3223f17.eps}
\end{figure}](/articles/aa/full/2003/12/aa3223/Timg92.gif) |
Figure 17: Lower panel: peak signal-to-noise ratio measured for the same star on a sequence of 150 s I images obtained with FORS1 on July 16, 2001. Solid and dashed lines trace Eq. (3) for U and I passbands respectively. Middle panel: seeing measured by the Differential Image Motion Monitor (DIMM, Sandrock et al. 2000) at 5500 Å and reported to zenith (empty circles); each point represents the average of DIMM data over the exposure time of each image. The solid circles indicate the image quality (FWHM) directly measured on the images. Upper panel: sky background (in ke-) measured on each image. |
| Open with DEXTER | |
Such abrupt phenomena, which make the sky brightness variations during a given
night rather unpredictable, are accompanied by more steady and well
behaved variations, the most clear of them being the inherent brightening
one faces going from small to large zenith distances.
In fact, as we have seen, the sky brightness increases at higher airmasses,
especially in the red passbands, where it can change by 0.4 mag going from
zenith to airmass X= 2. For a given object, as a result of the photon shot
noise increase, this turns into a degradation of the signal-to-noise ratio by
a factor 1.6, which could bring it below the detection limit. Unfortunately,
there are two other effects which work in the same direction, i.e. the
increase of atmospheric extinction and seeing degradation. While the former
causes a decrement of the signal, the latter tends to dilute a stellar image
on a larger number of pixels on the detector.
Combining Eq. (C.3), the usual atmospheric extinction law
![]() and the law which describes the variation of
seeing with airmass (
and the law which describes the variation of
seeing with airmass (
![]() ,
Roddier 1981) we can try to estimate
the overall effect on the expected signal-to-noise ratio at the central peak
of a stellar object. After very simple calculations, one obtains the following
expression:
,
Roddier 1981) we can try to estimate
the overall effect on the expected signal-to-noise ratio at the central peak
of a stellar object. After very simple calculations, one obtains the following
expression:
Acknowledgements
We are grateful to K. Krisciunas and B. Schaefer for the discussion about the implementation of their model and to Bruno Leibundgut, Dave Silva, Gero Rupprecht and Jean Gabriel Cuby for carefully reading the original manuscript. We wish to thank Reinhard Hanuschik for providing us with the high resolution UVES night sky spectrum before publication. We are finally deeply indebted to Martino Romaniello, for the illuminating discussions, useful advices and stimulating suggestions.All FORS1 images used in this paper were obtained during Service Mode runs and their proprietary period has expired.