Consider a cloud of plasma of electron density n at a temperature
T which covers a solid angle
![]() along the
line of sight to the observer at a distance R from the burst
explosion site (see Fig. 3). The luminosity that is
inferred from infinity, taking into account the light travel time
effects, is given by
along the
line of sight to the observer at a distance R from the burst
explosion site (see Fig. 3). The luminosity that is
inferred from infinity, taking into account the light travel time
effects, is given by![]() :
:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3193f2.eps}
\end{figure}](/articles/aa/full/2003/09/aa3193/Timg15.gif) |
Figure 2:
Photoionization optical depth of a |
In many astrophysically relevant situations (e.g. the IGM in
galaxy clusters),
![]() and both the heating and
cooling time scales are irrelevant and Eq. (1) simplifies to
the usual free-free equation:
and both the heating and
cooling time scales are irrelevant and Eq. (1) simplifies to
the usual free-free equation:
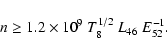 |
(7) |
In conclusion, a thermal component that contributes to the early
afterglow of a typical GRB cannot be emitted in the non-cooling
regime. In fact, in order to reach a luminosity large enough without
involving a too large thermal energy, the plasma density must be so
large as to make the cooling time very short. As an example, R02 derived
a cooling time of ![]() 2 s for the afterglow of GRB 011211. We cannot
therefore adopt the simple Eq. (2) but we must use the more
complete Eq. (1).
2 s for the afterglow of GRB 011211. We cannot
therefore adopt the simple Eq. (2) but we must use the more
complete Eq. (1).
We therefore consider in the following two limiting cases:
![]() (flash
heating) and
(flash
heating) and
![]() (steady heating). In principle also the case
(steady heating). In principle also the case
![]() may be
interesting. It is however difficult to identify a heating source that
can be active for a time comparable to the line emission
time scale. Even if the emitting plasma would be heated by afterglow
photons, the heating time could be at most a few per cent of the line
emission time scale (Lazzati et al. 2002b).
may be
interesting. It is however difficult to identify a heating source that
can be active for a time comparable to the line emission
time scale. Even if the emitting plasma would be heated by afterglow
photons, the heating time could be at most a few per cent of the line
emission time scale (Lazzati et al. 2002b).
![\begin{figure}
\par\includegraphics[width=13.7cm,clip]{3193f4.eps}
\end{figure}](/articles/aa/full/2003/09/aa3193/Timg30.gif) |
Figure 4:
The luminosity coefficient |
Consider a portion of a spherical shell of plasma of radius R,
temperature T and uniform density n covering a solid angle
![]() (see, again, Fig. 3). Its emission
integral can be written as
(see, again, Fig. 3). Its emission
integral can be written as
![]() where
where
![]() is the ratio of the thickness of the shell
to its radius
is the ratio of the thickness of the shell
to its radius![]() . Considering the values
. Considering the values
![]() defined above
(and shown in Fig. 1), the cloud will produce a line with
luminosity
defined above
(and shown in Fig. 1), the cloud will produce a line with
luminosity![]() (see Eq. (1)):
(see Eq. (1)):
Let us now consider a plasma in which a source of heating is active
for a time scale
![]() .
In the case of
radiative heating, this time scale may be for example the GRB duration
or even longer, if the afterglow photons can contribute to the
heating. In steady heating, the line luminosity (continuum luminosity
for
.
In the case of
radiative heating, this time scale may be for example the GRB duration
or even longer, if the afterglow photons can contribute to the
heating. In steady heating, the line luminosity (continuum luminosity
for
![]() )
can be written as:
)
can be written as:
To compare these results with afterglow data, consider a Fe line with
L=1045 erg s-1 (GRB 991216; Piro et al. 2000) or the S line
in GRB 011211 (R02) with luminosity
![]() erg s-1. In both cases a ratio
erg s-1. In both cases a ratio
![]() is required, by comparison with the
appropriate panel in Fig. 4. A typical heating time can be
considered to be the fireball transit time, which is equivalent to the
total duration of the prompt GRB emission. In both cases such duration
is of the order of
is required, by comparison with the
appropriate panel in Fig. 4. A typical heating time can be
considered to be the fireball transit time, which is equivalent to the
total duration of the prompt GRB emission. In both cases such duration
is of the order of ![]() 100 s, leaving us with an extreme requirement
of anisotropy
100 s, leaving us with an extreme requirement
of anisotropy
![]() .
Alternatively, the heating may be
provided radiatively by the absorption of GRB and early afterglow
photons. In that case, the duration of the heat supply may be of
several per cent of the line emission time scale (Lazzati et al. 2002b). In that case the constraint would be relaxed to the (yet
still challenging) value
.
Alternatively, the heating may be
provided radiatively by the absorption of GRB and early afterglow
photons. In that case, the duration of the heat supply may be of
several per cent of the line emission time scale (Lazzati et al. 2002b). In that case the constraint would be relaxed to the (yet
still challenging) value
![]() .
The most convenient
solution is represented by an (unknown) heating mechanism acting for a
time comparable to the line emission time scale itself. In this case,
the constraint on the geometric factor
.
The most convenient
solution is represented by an (unknown) heating mechanism acting for a
time comparable to the line emission time scale itself. In this case,
the constraint on the geometric factor ![]() would be similar to the
one derived above for the flash heating case. Such a heating mechanism
is however presently obscure and will have to face the problem of
stability discussed below (Sect. 4).
would be similar to the
one derived above for the flash heating case. Such a heating mechanism
is however presently obscure and will have to face the problem of
stability discussed below (Sect. 4).
In a steady heating scenario, therefore, thermal lines and continua can dominate the early afterglow emission, only in case of extreme geometric conditions, in which the emission is produced either in a sheet like shell or an extremely clumpy medium. Interestingly, analogous extreme conditions were independently inferred for the environment of GRB 000210 (Piro et al. 2002) in order to account for the lack of ionization features in the soft X-ray afterglow spectrum. Piro et al. (2002, and references therein) argue also that such conditions may be realized in giant molecular clouds. Stability considerations (see Sect. 4), however, show that more extreme conditions are required in this case. Unlike what is derived in the flash heating condition, in this case the radius of the shell does not have to be very large, and therefore the total mass required is not huge.
Copyright ESO 2003