In the above section we have derived some geometrical constraints on the emitting plasma in order to reproduce the observed features and continua. Since the results envisage particular geometric conditions, we here analyze their stability. First, since the heating energy is supposed to come from a central point (the GRB progenitor), one has to make sure that the emitting material is not accelerated to high velocities.
Consider a shell of mass M absorbing energy from a relativistic
outflow. If the material is radiative, it acquires a bulk velocity
v=E/(M c). A bulk velocity
![]() was measured in
GRB 011211 (R02) and GRB 991216 (Piro et al. 2000). Requiring that our
optically thin shell is accelerated to a comparable or smaller speed
implies a radius larger than:
was measured in
GRB 011211 (R02) and GRB 991216 (Piro et al. 2000). Requiring that our
optically thin shell is accelerated to a comparable or smaller speed
implies a radius larger than:
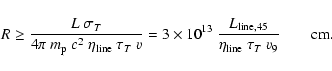 |
(10) |
Provided that the emitting medium is not accelerated to relativistic
speeds by the energy input, we also want that the thin emitting shell
(or blobs) do not expand in a time scale smaller than the emission one
(which can be either the heating or cooling time scale). The shell
(or blobs) was in fact in equilibrium with the ambient medium when it
was cold. Now that its temperature is increased it will tend to expand
under the effect of the increased internal pressure. If it expands at
the speed of sound ![]() ,
its density will be sizably modified in a
time scale
,
its density will be sizably modified in a
time scale
![]() .
It is therefore required
that the expansion time is longer than the emission time scale.
.
It is therefore required
that the expansion time is longer than the emission time scale.
In the case of steady heating we obtain:
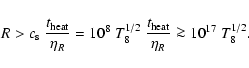 |
(11) |
| (12) |
Copyright ESO 2003