We illustrate in Fig. 2 results obtained for a model
without any magnetic fields and without mass sink.
A strong outflow develops even in this case,
which is driven mostly by the vertical pressure gradient in
the transition layer between the disc and the corona, in particular by the term
![]() in Eq. (21).
The gain in velocity is controlled by the total
specific entropy difference between the disc and the corona, but not by
the thickness d of the transition layer in the disc profile
(4).
in Eq. (21).
The gain in velocity is controlled by the total
specific entropy difference between the disc and the corona, but not by
the thickness d of the transition layer in the disc profile
(4).
The flow is fastest along the rotation axis and within a cone of polar
angle of about ![]() ,
where the terminal velocity
,
where the terminal velocity
![]() is reached.
The conical shape of the outflow is partly due to obstruction from
the dense disc, making it easier for matter to leave the
disc near the axis. Both temperature and
density in nonmagnetic runs without mass sink are reduced very
close to the axis
where the flow speed is highest.
is reached.
The conical shape of the outflow is partly due to obstruction from
the dense disc, making it easier for matter to leave the
disc near the axis. Both temperature and
density in nonmagnetic runs without mass sink are reduced very
close to the axis
where the flow speed is highest.
The general flow pattern is sensitive to whether or not matter can accrete
onto the central object. We show in Fig. 3 results for the
same model as in Fig. 2, but with a mass sink given by Eq. (6)
with
![]() .
This can be compared with earlier work on thermally driven winds by
Fukue (1989) who also considered polytropic outflows, but the disc
was treated as a boundary condition. In Fukue (1989), outflows are driven when the
injected energy is above a critical value. The origin of this
energy injection may be a hot corona. The critical surface in
his model (see the lower panel of his Fig. 2) is quite similar
to that found in our simulation (our Fig. 3), although
our opening angle was found to be larger than in Fukue's (1989) model.
(Below we show, albeit with magnetic fields, that smaller values
of
.
This can be compared with earlier work on thermally driven winds by
Fukue (1989) who also considered polytropic outflows, but the disc
was treated as a boundary condition. In Fukue (1989), outflows are driven when the
injected energy is above a critical value. The origin of this
energy injection may be a hot corona. The critical surface in
his model (see the lower panel of his Fig. 2) is quite similar
to that found in our simulation (our Fig. 3), although
our opening angle was found to be larger than in Fukue's (1989) model.
(Below we show, albeit with magnetic fields, that smaller values
of ![]() do result in smaller opening angles, see Fig. 9,
which would then be compatible with the result of Fukue (1989).)
do result in smaller opening angles, see Fig. 9,
which would then be compatible with the result of Fukue (1989).)
As could be expected, the mass sink hampers the outflow in the cone (but not at
![]() ).
The flow remains very similar to that of Fig. 3 when
).
The flow remains very similar to that of Fig. 3 when
![]() is reduced
to 0.005.
Thus, the nonmagnetic outflows are very sensitive to the presence of the
central sink.
As we show now, magnetized outflows are different in this respect.
is reduced
to 0.005.
Thus, the nonmagnetic outflows are very sensitive to the presence of the
central sink.
As we show now, magnetized outflows are different in this respect.
In this section we discuss results obtained with magnetic fields,
first without mass sink at the centre
and then including a sink. We show that the effects of the sink are
significantly weaker than in the nonmagnetic case.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f4.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg247.gif) |
Figure 4:
A magnetic model without mass sink at the centre:
velocity vectors and poloidal magnetic field lines (white)
superimposed on a grey scale representation of
temperature (in terms of h) for a run with
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f5.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg248.gif) |
Figure 5:
Profiles of vertical velocity and sound speed along
the axis, |
![\begin{figure}
\par\includegraphics[width=18cm,clip]{AA9940f6.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg249.gif) |
Figure 6:
Results for a larger domain,
|
A magnetized outflow without the central mass sink, shown in Fig. 4, is similar
to that in Fig. 2, but is denser and hotter near the axis,
and the high speed cone has a somewhat larger opening angle.
In addition, the outflow becomes more structured, with a well pronounced
conical shell where temperature and density are smaller than elsewhere
(the conical shell reaches
![]() at
at
![]() in Fig. 4).
Here and in some of the following figures we also show the fast
magnetosonic surface with respect to the poloidal field.
In Sect. 3.5 we show that this surface is close
to the fast magnetosonic surface.
As shown in Fig. 5, the outflow becomes
faster inside the cone (
in Fig. 4).
Here and in some of the following figures we also show the fast
magnetosonic surface with respect to the poloidal field.
In Sect. 3.5 we show that this surface is close
to the fast magnetosonic surface.
As shown in Fig. 5, the outflow becomes
faster inside the cone (
![]() on the axis).
As expected, we find that
deeper potential wells, i.e. smaller values of r0 in Eq. (5) and (23),
result in even faster flows
and in larger opening angles.
on the axis).
As expected, we find that
deeper potential wells, i.e. smaller values of r0 in Eq. (5) and (23),
result in even faster flows
and in larger opening angles.
Our results are insensitive to the size and symmetry of the computational domain: we
illustrate this in Fig. 6 with a larger
domain of the size
![]() .
The disc midplane in this run is located asymmetrically in zin order to verify that the (approximate) symmetry of the solutions
is not imposed by the symmetry of the computational domain. Figure 6 confirms that our results
are not affected by what happens near the computational boundaries.
.
The disc midplane in this run is located asymmetrically in zin order to verify that the (approximate) symmetry of the solutions
is not imposed by the symmetry of the computational domain. Figure 6 confirms that our results
are not affected by what happens near the computational boundaries.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{AA9940f7.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg251.gif) |
Figure 7:
As in Fig. 4, but with a mass sink at the centre,
|
Unlike the nonmagnetized system, the magnetized outflow changes only comparatively
little when the mass sink is introduced at the centre. We show in Fig. 7
the results with a sink (
![]() )
and otherwise the same
parameters as in Fig. 4.
As could be expected, the sink leads to a
reduction in the outflow speed near the axis; the flow in the high speed cone becomes slower.
But apart from that, the most
important effects of the sink are the enhancement of the conical structure of the
outflow and the smaller opening angle of the conical shell.
A decrease in
)
and otherwise the same
parameters as in Fig. 4.
As could be expected, the sink leads to a
reduction in the outflow speed near the axis; the flow in the high speed cone becomes slower.
But apart from that, the most
important effects of the sink are the enhancement of the conical structure of the
outflow and the smaller opening angle of the conical shell.
A decrease in
![]() by a factor of 2 to 0.005 has very little effect,
as illustrated in Figs. 8 and 10.
by a factor of 2 to 0.005 has very little effect,
as illustrated in Figs. 8 and 10.
Increasing the entropy contrast (while keeping the specific entropy unchanged in the corona)
reduces the opening angle of the conical shell.
Pressure driving is obviously more important in this case, as compared
to magneto-centrifugal driving (see Sect. 3.5).
A model with
![]() (corresponding to a density and inverse temperature
contrast of about 50:1 between the disc and the corona) is shown in
Fig. 9.
At
(corresponding to a density and inverse temperature
contrast of about 50:1 between the disc and the corona) is shown in
Fig. 9.
At
![]() ,
the radial velocity
,
the radial velocity ![]() is slightly
enhanced relative to the case
is slightly
enhanced relative to the case ![]() (contrast 10:1);
see Fig. 10.
At
(contrast 10:1);
see Fig. 10.
At
![]() ,
on the other hand, the flow with the larger entropy contrast
reaches the Alfvén point close to the disc (at
,
on the other hand, the flow with the larger entropy contrast
reaches the Alfvén point close to the disc (at
![]() as opposed to
as opposed to ![]() in the other case), which leads to a smaller terminal velocity.
in the other case), which leads to a smaller terminal velocity.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f8.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg254.gif) |
Figure 8:
As in Fig. 7, but with a stronger mass sink at the centre,
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f9.eps}
\end{figure}](/articles/aa/full/2003/06/aa9940/Timg255.gif) |
Figure 9:
As in Fig. 7, but with a larger entropy contrast,
|
We conclude that the general structure of the
magnetized flow and its typical parameters
remain largely unaffected by the sink, provided its efficiency
![]() does not exceed a certain threshold.
It is plausibly the build-up of magnetic pressure at the centre that shields the central
object to make the central accretion inefficient. This shielding would be
even stronger if we included a magnetosphere of the central object. We discuss in
Sect. 4.1 the dependence of our solution on the geometrical size of the sink and
show that the general structure of the outflow persists as long as the size of the sink does
not exceed the disk thickness.
does not exceed a certain threshold.
It is plausibly the build-up of magnetic pressure at the centre that shields the central
object to make the central accretion inefficient. This shielding would be
even stronger if we included a magnetosphere of the central object. We discuss in
Sect. 4.1 the dependence of our solution on the geometrical size of the sink and
show that the general structure of the outflow persists as long as the size of the sink does
not exceed the disk thickness.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{AA9940f10.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg257.gif) |
Figure 10:
Spherical radial velocity component, |
The dynamo in most of our models has
![]() ,
consistent with results from simulations of
disc turbulence driven by the magneto-rotational instability
(Brandenburg et al. 1995; Ziegler & Rüdiger 2000). The
resulting field symmetry is roughly dipolar,
which seems to be typical of
,
consistent with results from simulations of
disc turbulence driven by the magneto-rotational instability
(Brandenburg et al. 1995; Ziegler & Rüdiger 2000). The
resulting field symmetry is roughly dipolar,
which seems to be typical of
![]() disc
dynamos with
disc
dynamos with
![]() in a conducting corona (e.g., Brandenburg et al. 1990). We note that the dominant parity of the magnetic field is sensitive
to the magnetic diffusivity in the corona: a
quadrupolar oscillatory magnetic field dominates for
in a conducting corona (e.g., Brandenburg et al. 1990). We note that the dominant parity of the magnetic field is sensitive
to the magnetic diffusivity in the corona: a
quadrupolar oscillatory magnetic field dominates for
![]() if the disc is surrounded by vacuum (Stepinski & Levy 1988).
if the disc is surrounded by vacuum (Stepinski & Levy 1988).
For
![]() ,
the critical value of
,
the critical value of ![]() for dynamo action is
about 0.2, which is a factor of about 50 larger than without
outflows.
Our dynamo is then only less than twice supercritical. A
survey of the dynamo regimes for similar models is given by
Bardou et al. (2001).
for dynamo action is
about 0.2, which is a factor of about 50 larger than without
outflows.
Our dynamo is then only less than twice supercritical. A
survey of the dynamo regimes for similar models is given by
Bardou et al. (2001).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f11.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg260.gif) |
Figure 11:
Radial profiles of magnetic pressure from the toroidal (solid) and poloidal (dotted)
magnetic fields and thermal pressure (dashed) for the model of Fig. 6.
Shown are the averages over the disc volume (lower panel) and
over a region of the same size around z=8 in the corona (upper panel). |
The initial magnetic field (poloidal, mixed parity) is weak
(
![]() ), cf. Fig. 11
for comparison with the gas pressure],
but the dynamo soon amplifies the field in the
disc to
), cf. Fig. 11
for comparison with the gas pressure],
but the dynamo soon amplifies the field in the
disc to
![]() ,
and then supplies it to the corona. As a result, the corona is
filled with a predominantly azimuthal field with
,
and then supplies it to the corona. As a result, the corona is
filled with a predominantly azimuthal field with
![]() at larger radii; see
Fig. 11. We note, however, that the flow in the corona varies significantly in
both space and time
at larger radii; see
Fig. 11. We note, however, that the flow in the corona varies significantly in
both space and time![]() . Magnetic pressure due to the toroidal field
. Magnetic pressure due to the toroidal field ![]() ,
,
![]() ,
exceeds
gas pressure in the corona outside the inner cone
and confines the outflow in the conical shell. The main mechanisms producing
,
exceeds
gas pressure in the corona outside the inner cone
and confines the outflow in the conical shell. The main mechanisms producing
![]() in the corona are advection by the wind and magnetic buoyancy (cf. Moss
et al. 1999). Magnetic diffusion and stretching of the poloidal field by
vertical shear play a relatively unimportant rôle.
in the corona are advection by the wind and magnetic buoyancy (cf. Moss
et al. 1999). Magnetic diffusion and stretching of the poloidal field by
vertical shear play a relatively unimportant rôle.
The field in the inner parts of the disc is dominated by the toroidal component;
![]() at
at
![]() ;
this ratio is larger
in the corona at all
;
this ratio is larger
in the corona at all ![]() .
However, as shown in Fig. 11, this ratio is closer to unity at larger radii
in the disc.
.
However, as shown in Fig. 11, this ratio is closer to unity at larger radii
in the disc.
As expected,
![]() results in mostly quadrupolar fields (e.g., Ruzmaikin
et al. 1988). As shown in Fig. 12, the magnetic field in the corona
is now mainly restricted to a narrow conical shell that crosses
results in mostly quadrupolar fields (e.g., Ruzmaikin
et al. 1988). As shown in Fig. 12, the magnetic field in the corona
is now mainly restricted to a narrow conical shell that crosses ![]() at
at
![]() .
Comparing this figure with the results
obtained with dipolar magnetic fields (Fig. 4),
one sees that the quadrupolar field has
a weaker effect on the outflow than the dipolar field; the conical shell is less pronounced.
However, the structures within the inner cone are qualitatively similar to each other.
.
Comparing this figure with the results
obtained with dipolar magnetic fields (Fig. 4),
one sees that the quadrupolar field has
a weaker effect on the outflow than the dipolar field; the conical shell is less pronounced.
However, the structures within the inner cone are qualitatively similar to each other.
The magnitude and distribution of ![]() in Eq. (14) only weakly
affect magnetic field properties as far as the dynamo is saturated. For a saturated dynamo, the
field distribution in the dynamo region (
in Eq. (14) only weakly
affect magnetic field properties as far as the dynamo is saturated. For a saturated dynamo, the
field distribution in the dynamo region (
![]() ,
|z|<0.15)
roughly follows from the equipartition field,
,
|z|<0.15)
roughly follows from the equipartition field,
![]() with
with
![]() .
In other words, nonlinear states of disc dynamos are almost insensitive to the
detailed properties of
.
In other words, nonlinear states of disc dynamos are almost insensitive to the
detailed properties of ![]() (e.g., Beck et al. 1996; Ruzmaikin et al. 1988).
(e.g., Beck et al. 1996; Ruzmaikin et al. 1988).
A discussion of disc dynamos with outflows, motivated by the present model, can
be found in Bardou et al. (2001). It is shown that the value of magnetic
diffusivity in the corona does not affect the dynamo solutions strongly.
Moreover, the outflow is fast enough to have the magnetic Reynolds number
in the corona larger than unity, which implies that ideal integrals
of motion are very nearly constant along field lines;
see Sect. 3.6. The most important
property is the sign of ![]() as it controls the global symmetry of the
magnetic field.
as it controls the global symmetry of the
magnetic field.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f12.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg271.gif) |
Figure 12:
As in Fig. 4, but with
|
The mass injection and loss rates
due to the source, sink and wind are defined as
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{AA9940f13.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg275.gif) |
Figure 13:
Azimuthally integrated mass flux density, represented as a vector
|
The mass loss rate in the wind fluctuates on a time
scale of 5 time units,
but remains constant on average at about
![]() ,
corresponding
to
,
corresponding
to
![]() ,
in the models of Figs. 7 and 8.
The mass
in the disc,
,
in the models of Figs. 7 and 8.
The mass
in the disc,
![]() ,
remains roughly constant.
,
remains roughly constant.
The rate at which mass needs to
be replenished in the disc,
![]() ,
is about 0.4.
This rate is not controlled by
the imposed response rate of the mass source,
,
is about 0.4.
This rate is not controlled by
the imposed response rate of the mass source,
![]() ,
which is 25 times larger. So,
the mass source adjusts itself to the disc evolution and does not directly
control the outflow.
We show in Fig. 13 trajectories that start in and around the
mass injection region.
The spatial distribution of the mass replenishment rate
,
which is 25 times larger. So,
the mass source adjusts itself to the disc evolution and does not directly
control the outflow.
We show in Fig. 13 trajectories that start in and around the
mass injection region.
The spatial distribution of the mass replenishment rate
![]() shown in Fig. 13 indicates that
the mass is mainly injected close to the mass sink, and
shown in Fig. 13 indicates that
the mass is mainly injected close to the mass sink, and
![]() remains moderate in the outer parts of the disc.
(Note that the reduced effect of the mass sink in the magnetized flow
is due to magnetic shielding rather than to mass replenishment near
the sink - see Sect. 3.2.)
remains moderate in the outer parts of the disc.
(Note that the reduced effect of the mass sink in the magnetized flow
is due to magnetic shielding rather than to mass replenishment near
the sink - see Sect. 3.2.)
The angular structure of the outflow can be characterized by the following
quantities calculated for a particular spherical
radius, r=8,
for the model of Fig. 6: the azimuthally integrated normalized
radial mass flux density,
![]() ,
where
,
where
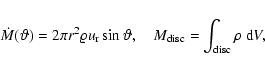 |
(38) |
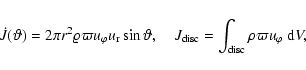 |
(39) |
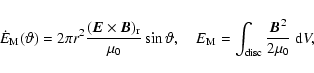 |
(40) |
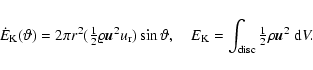 |
(41) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f14.eps}
\end{figure}](/articles/aa/full/2003/06/aa9940/Timg296.gif) |
Figure 14:
Dependence, on polar angle |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f15.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg297.gif) |
Figure 15:
Angular momentum (normalized by the maximum angular momentum in the disc)
for the model with
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f16.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg300.gif) |
Figure 16:
The ratio of the poloidal magneto-centrifugal and pressure forces,
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f17.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg303.gif) |
Figure 17:
The ratio
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f18.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg304.gif) |
Figure 18:
As in Fig. 16, but for the model of
Fig. 9, i.e. with larger entropy contrast,
|
The radial kinetic and magnetic energy flux densities, integrated over the whole sphere,
are
![]() and
and
![]() ,
respectively, where
,
respectively, where
![]() is
the fast magnetosonic speed (with respect to the poloidal field)
at the critical surface (where uz=c*) on the axis.
Thus,
is
the fast magnetosonic speed (with respect to the poloidal field)
at the critical surface (where uz=c*) on the axis.
Thus,
![]() can be taken as a good indicator of the kinetic energy
loss, and the magnetic energy loss into the exterior is about 3% of this value.
These surface-integrated flux densities (or luminosities) are, as expected,
roughly independent of the distance from the central object.
can be taken as a good indicator of the kinetic energy
loss, and the magnetic energy loss into the exterior is about 3% of this value.
These surface-integrated flux densities (or luminosities) are, as expected,
roughly independent of the distance from the central object.
The magnetized outflows in our models with central mass sink have a well-pronounced structure, with a fast, cool and low-density flow in a conical shell, and a slower, hotter and denser flow near the axis and in the outer parts of the domain. Without central mass sink, there is a high speed, hot and dense cone around the axis.
The magnetic field geometry (e.g., Fig. 7) is
such that for
![]() ,
the angle between the disc surface and the
field lines is less than
,
the angle between the disc surface and the
field lines is less than ![]() ,
reaching
,
reaching
![]() at
at
![]() -1.5, which is favourable for
magneto-centrifugal acceleration (Blandford & Payne 1982;
Campbell 1999, 2000, 2001).
However, the Alfvén surface is so close to the disc surface in the outer parts
of the disc that acceleration there is mainly due to pressure gradient.
The situation is, however, different in the conical shell containing the fast wind.
As can be seen from Fig. 15, the Alfvén surface is
far away from the disc in that region and,
on a given field line,
the Alfvén radius is at least a few times larger than
the radius of the footpoint in the disc.
This is also seen in simulations of the magneto-centrifugally driven jets of
Krasnopolsky et al. (1999);
see their Fig. 4.
The lever arm of about 3 is sufficient for magneto-centrifugal driving
to dominate.
As can be seen also from Fig. 10,
the flow at the polar angle
-1.5, which is favourable for
magneto-centrifugal acceleration (Blandford & Payne 1982;
Campbell 1999, 2000, 2001).
However, the Alfvén surface is so close to the disc surface in the outer parts
of the disc that acceleration there is mainly due to pressure gradient.
The situation is, however, different in the conical shell containing the fast wind.
As can be seen from Fig. 15, the Alfvén surface is
far away from the disc in that region and,
on a given field line,
the Alfvén radius is at least a few times larger than
the radius of the footpoint in the disc.
This is also seen in simulations of the magneto-centrifugally driven jets of
Krasnopolsky et al. (1999);
see their Fig. 4.
The lever arm of about 3 is sufficient for magneto-centrifugal driving
to dominate.
As can be seen also from Fig. 10,
the flow at the polar angle
![]() is mainly accelerated by pressure gradient
near the disc surface
(where the Alfvén surface is close to the disc surface).
However, acceleration remains efficient out to at least r=1within the conical shell at
is mainly accelerated by pressure gradient
near the disc surface
(where the Alfvén surface is close to the disc surface).
However, acceleration remains efficient out to at least r=1within the conical shell at
![]() .
This can be seen in the upper and middle
panels of Fig. 10 (note that the conical shell is thinner and at a smaller
.
This can be seen in the upper and middle
panels of Fig. 10 (note that the conical shell is thinner and at a smaller ![]() in the model with larger
entropy contrast, and so it cannot be seen in this figure, cf. Fig. 9).
These facts strongly indicate that magneto-centrifugal acceleration dominates
within the conical shell.
in the model with larger
entropy contrast, and so it cannot be seen in this figure, cf. Fig. 9).
These facts strongly indicate that magneto-centrifugal acceleration dominates
within the conical shell.
Another indicator of magneto-centrifugal acceleration in the conical shell is the distribution
of angular momentum (see Fig. 15), which is significantly larger in the outer parts of
the conical shell than in the disc, which suggests that the magnetic field plays
an important rôle in the flow dynamics. We
show in Fig. 16 the ratio of the "magneto-centrifugal force''
to pressure gradient,
![]() ,
where
the subscript "pol'' denotes the poloidal components.
Here, the "magneto-centrifugal force'' includes all terms in the
poloidal equation of motion, except for the pressure gradient (but we ignore
the viscous term and the mass production term, the latter being
restricted to the disc only),
,
where
the subscript "pol'' denotes the poloidal components.
Here, the "magneto-centrifugal force'' includes all terms in the
poloidal equation of motion, except for the pressure gradient (but we ignore
the viscous term and the mass production term, the latter being
restricted to the disc only),
As further evidence of a significant contribution from
magneto-centrifugal driving in the conical shell, we show in Fig. 17
that the magnetic field is close to a force-free configuration in regions where
angular momentum is enhanced, i.e. in the conical shell and in the corona surrounding
the outer parts of the disc. These are the regions where the Lorentz force contributes
significantly to the flow dynamics, so that the magnetic field performs work and therefore relaxes
to a force-free configuration.
The radial variation in the sign of the current helicity
![]() is due to
a variation in the sign of the azimuthal magnetic field and of the current
density.
Such changes originate from the disc where they
imprint a corresponding variation in the sign of the
angular momentum constant, see Eq. (46).
These variations are then carried along magnetic lines into the corona.
The locations where the azimuthal field reverses are still relatively
close to the axis, and there the azimuthal field relative to the poloidal field
is weak compared to
regions further away from the axis.
is due to
a variation in the sign of the azimuthal magnetic field and of the current
density.
Such changes originate from the disc where they
imprint a corresponding variation in the sign of the
angular momentum constant, see Eq. (46).
These variations are then carried along magnetic lines into the corona.
The locations where the azimuthal field reverses are still relatively
close to the axis, and there the azimuthal field relative to the poloidal field
is weak compared to
regions further away from the axis.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f19.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg324.gif) |
Figure 19:
Flow parameters as functions of height z, along the field line with its footpoint at
|
Pressure driving is more important if the entropy contrast between
the disc and the corona is larger (i.e. ![]() is smaller): the white conical shell
in Fig. 16
indicative of stronger magneto-centrifugal driving shifts to larger heights for
is smaller): the white conical shell
in Fig. 16
indicative of stronger magneto-centrifugal driving shifts to larger heights for
![]() ,
as shown in Fig. 18. We note, however, that there
are periods when magneto-centrifugal driving is dominant even in this
model with higher entropy contrast, but pressure driving dominates in the
time averaged picture (at least within our computational domain).
,
as shown in Fig. 18. We note, however, that there
are periods when magneto-centrifugal driving is dominant even in this
model with higher entropy contrast, but pressure driving dominates in the
time averaged picture (at least within our computational domain).
We show in Fig. 19 the variation of several quantities along
a magnetic field line that has its footpoint at the disc
surface at
![]() and lies around the conical shell.
Since this is where magneto-centrifugal driving is still dominant, it is useful
to compare Fig. 19 with Fig. 3 of Ouyed et al. (1997), where a
well-collimated magneto-centrifugal jet is studied.
Since our outflow is collimated only weakly within our computational domain,
the quantities are plotted against height z, rather than
and lies around the conical shell.
Since this is where magneto-centrifugal driving is still dominant, it is useful
to compare Fig. 19 with Fig. 3 of Ouyed et al. (1997), where a
well-collimated magneto-centrifugal jet is studied.
Since our outflow is collimated only weakly within our computational domain,
the quantities are plotted against height z, rather than ![]() as in
Ouyed et al. (1997) (
as in
Ouyed et al. (1997) (![]() is nearly constant along a field line for weakly collimated
flows, whereas approximately
is nearly constant along a field line for weakly collimated
flows, whereas approximately
![]() along a magnetic line for well-collimated flows).
The results are qualitatively similar, with the main difference that
the fast magnetosonic surface in our model almost coincides with the Alfvén surface
in the region around the conical shell where the outflow is highly supersonic.
Since we include finite diffusivity, the curves in Fig. 19 are smoother
than in Ouyed et al. (1997), who consider ideal MHD.
A peculiar feature of the conical shell is that the flow at
along a magnetic line for well-collimated flows).
The results are qualitatively similar, with the main difference that
the fast magnetosonic surface in our model almost coincides with the Alfvén surface
in the region around the conical shell where the outflow is highly supersonic.
Since we include finite diffusivity, the curves in Fig. 19 are smoother
than in Ouyed et al. (1997), who consider ideal MHD.
A peculiar feature of the conical shell is that the flow at ![]() is sub-Alfvénic
but strongly supersonic.
The fast magnetosonic surface is where the poloidal
velocity
is sub-Alfvénic
but strongly supersonic.
The fast magnetosonic surface is where the poloidal
velocity
![]() equals the fast magnetosonic speed for the
direction parallel to the field lines,
equals the fast magnetosonic speed for the
direction parallel to the field lines,
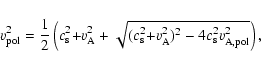 |
(43) |
Axisymmetric ideal magnetized outflows are governed by five
Lagrangian invariants,
the flux ratio,
| (44) |
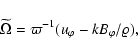 |
(45) |
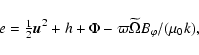 |
(47) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{aa9940f20.eps}\end{figure}](/articles/aa/full/2003/06/aa9940/Timg339.gif) |
Figure 20:
The four Lagrangian invariants k(a),
|
We show in Fig. 20 scatter plots of k(a),
![]() ,
,
![]() ,
and e(a)for the model of Fig. 6.
Points from the region
,
and e(a)for the model of Fig. 6.
Points from the region
![]() collapse into a single line, confirming that
the flow in the corona is nearly ideal
collapse into a single line, confirming that
the flow in the corona is nearly ideal![]() .
This is not surprising since
the magnetic Reynolds number is much greater than
unity in the corona
for the parameters adopted here.
For
.
This is not surprising since
the magnetic Reynolds number is much greater than
unity in the corona
for the parameters adopted here.
For
![]() ,
there are departures from perfect MHD; in particular, the
angular velocity of magnetic field lines,
,
there are departures from perfect MHD; in particular, the
angular velocity of magnetic field lines,
![]() ,
is somewhat decreased in the upper parts of the domain
(indicated by the vertical scatter in the data points).
This is plausibly due to the finite magnetic diffusivity which still
allows matter to slightly lag behind the magnetic field.
As this lag accumulates along a stream line, the departures increase with
height z.
Since this is a "secular'' effect only, and accumulates with height, we locally
still have little variation of k and
,
is somewhat decreased in the upper parts of the domain
(indicated by the vertical scatter in the data points).
This is plausibly due to the finite magnetic diffusivity which still
allows matter to slightly lag behind the magnetic field.
As this lag accumulates along a stream line, the departures increase with
height z.
Since this is a "secular'' effect only, and accumulates with height, we locally
still have little variation of k and
![]() ,
which explains why
magneto-centrifugal acceleration can operate quite efficiently.
,
which explains why
magneto-centrifugal acceleration can operate quite efficiently.
The corona in our model has (turbulent) magnetic diffusivity comparable to that in the disc. This is consistent with, e.g., Ouyed & Pudritz (1999) who argue that turbulence should be significant in coronae of accretion discs. Nevertheless, it turns out that ideal MHD is a reasonable approximation for the corona (see Fig. 20), but not for the disc. Therefore, magnetic diffusivity is physically significant in the disc and insignificant in the corona (due to different velocity and length scales involved), as in most models of disc outflows (see Ferreira & Pelletier 1995 for a discussion). Thus, our model confirms this widely adopted idealization.
Copyright ESO 2003