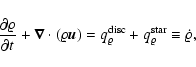 |
(1) |
Our intention is to make our model as simple as possible and to avoid
detailed modelling of mass supply to the accretion disc, which occurs
differently in different accreting systems. For example,
matter enters the accretion disc
at large radii in a restricted range of azimuthal angles in binary systems
with Roche lobe overflow. On the other hand, matter supply
can be more uniform in both azimuth and radius in active galactic nuclei.
Being interested in other aspects of accretion physics, we prefer to avoid
detailed modelling of these processes. Instead,
similarly to the model of Ouyed & Pudritz
(1997a, 1997b), we inject matter into the system, but an important difference is that
we introduce a self-regulating mass source in the disc.
We also allow for a mass sink at the centre to model
accretion onto the central object (star). With these two effects included,
the continuity equation becomes
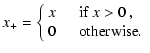 |
(3) |
In Eq. (2),
![]() is a response time which is chosen to
be significantly shorter than the time scale of the depletion processes,
which is equivalent to
the time scale of mass replenishment in the disc,
is a response time which is chosen to
be significantly shorter than the time scale of the depletion processes,
which is equivalent to
the time scale of mass replenishment in the disc,
![]() (cf. Sect. 3.4),
to avoid unphysical influences of the mass source. We do
not fix the distribution and magnitude of
(cf. Sect. 3.4),
to avoid unphysical influences of the mass source. We do
not fix the distribution and magnitude of
![]() beforehand, but the system adjusts itself such as to prevent the disc
from disappearing.
beforehand, but the system adjusts itself such as to prevent the disc
from disappearing.
The self-regulating mass sink at the position of the central star
is modelled in a similar manner,
Apart from the continuity Eq. (1), the mass source also appears
in the Navier-Stokes equation, unless matter is always injected with the
ambient velocity of the gas. In that case, however, a runaway instability
can occur: if matter is already slower than Keplerian, it falls inward, and so
does the newly injected matter. This enhances the need for even more mass
injection. A similar argument applies also if matter is rotating faster
than Keplerian. This is why we inject matter at the Keplerian speed.
This leads to an extra term in the Navier-Stokes equation,
![]() ,
which would only
be absent if the gas were rotating at the Keplerian speed. Thus,
the Navier-Stokes equation takes the form
,
which would only
be absent if the gas were rotating at the Keplerian speed. Thus,
the Navier-Stokes equation takes the form
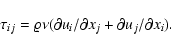 |
(8) |
| (9) |
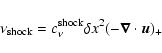 |
(12) |
We assume that the magnetic field in the disc is generated by
a standard
![]() -dynamo (e.g., Krause & Rädler 1980),
which implies an extra electromotive force,
-dynamo (e.g., Krause & Rädler 1980),
which implies an extra electromotive force,
![]() ,
in the
induction equation for the mean magnetic field,
,
in the
induction equation for the mean magnetic field, ![]() .
To ensure that
.
To ensure that ![]() is solenoidal, we solve the
induction equation in terms of the vector potential
is solenoidal, we solve the
induction equation in terms of the vector potential ![]() ,
,
Since
![]() has to be
antisymmetric about the midplane and vanishing outside the disc,
we adopt the form
has to be
antisymmetric about the midplane and vanishing outside the disc,
we adopt the form
Depending on the sign of ![]() and the vertical distribution of
and the vertical distribution of ![]() ,
the dynamo can
generate magnetic fields of either dipolar or quadrupolar symmetry.
We shall discuss both types of geometry.
,
the dynamo can
generate magnetic fields of either dipolar or quadrupolar symmetry.
We shall discuss both types of geometry.
Protostellar systems are known to be
strong X-ray sources (see, e.g., Glassgold et al. 2000;
Feigelson & Montmerle 1999; Grosso et al. 2000).
The X-ray emission is generally attributed to coronae of disc-star
systems, plausibly heated by small scale magnetic reconnection events
(Galeev et al. 1979), for example in the form of nanoflares
that are caused by slow footpoint motions (Parker 1994).
Heating of disc coronae by fluctuating magnetic
fields is indeed quite natural if one accepts that the disc
turbulence is caused by the magneto-rotational instability.
Estimates for the coronal temperatures of YSOs range from
![]() to
to
![]() (see, e.g., Feigelson & Montmerle 1999).
For the base of the disc corona, temperatures
of at least
(see, e.g., Feigelson & Montmerle 1999).
For the base of the disc corona, temperatures
of at least
![]() are to be expected in order to explain
the observed mass loss rates (Kwan & Tademaru 1995; Kwan 1997).
The discs, on the other hand, have typical temperatures of a few
are to be expected in order to explain
the observed mass loss rates (Kwan & Tademaru 1995; Kwan 1997).
The discs, on the other hand, have typical temperatures of a few
![]() (e.g., Papaloizou & Terquem 1999).
(e.g., Papaloizou & Terquem 1999).
A simple way to implement a dense, relatively cool disc embedded in a rarefied, hot
corona without modelling
the detailed physics of coronal heating is to prescribe the
distribution of specific entropy,
![]() ,
such that s is smaller
within the disc and larger in the corona.
For a perfect gas this implies
,
such that s is smaller
within the disc and larger in the corona.
For a perfect gas this implies
![]() (in a dimensionless form), where
(in a dimensionless form), where
![]() is a function of position
(here p and
is a function of position
(here p and ![]() are gas pressure and
density,
are gas pressure and
density,
![]() ,
and
,
and ![]() and
and ![]() are the
specific heats at constant pressure and constant volume, respectively).
are the
specific heats at constant pressure and constant volume, respectively).
We prescribe the polytrope parameter K to be unity in the
corona and smaller in the disc, so we put
In the present case it is advantageous to use the potential enthalpy,
| (17) |
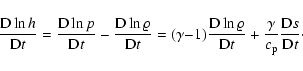 |
(18) |
The first law of thermodynamics allows us to
express the pressure gradient in terms of
h and s,
We use a softened, spherically symmetric gravitational potential of the form
Our initial state is the hydrostatic equilibrium obtained by
solving, for h, the vertical balance equation obtained from Eq. (22),
The
initial rotation velocity,
![]() ,
follows from the radial
balance equation,
,
follows from the radial
balance equation,
As a rough estimate, the value of h in the midplane of the
disc is
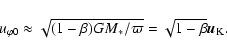 |
(27) |
Our model is scale invariant and can therefore be applied to various
astrophysical objects.
We consider here the range of parameters typical of protostellar discs, for which a typical
surface density is
![]() .
A typical coronal sound speed is
.
A typical coronal sound speed is
![]() ,
which corresponds to a temperature of
,
which corresponds to a temperature of
![]() .
This allows us to fix relevant units as follows:
.
This allows us to fix relevant units as follows:
Since [h]=[u]2,
the dimensionless value h=1 corresponds
to
![]() .
With a mean specific weight
.
With a mean specific weight ![]() ,
the universal gas constant
,
the universal gas constant
![]() and
and
![]() ,
we have
,
we have
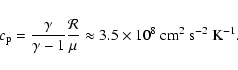 |
(29) |
We choose ![]() between 0.1 and 0.005, corresponding to
a typical disc temperature (in the model) of
between 0.1 and 0.005, corresponding to
a typical disc temperature (in the model) of
![]() to
to
![]() ;
see Eq. (26);
real
protostellar discs have typical temperatures of about a few
thousand Kelvin (see Sect. 2.2).
;
see Eq. (26);
real
protostellar discs have typical temperatures of about a few
thousand Kelvin (see Sect. 2.2).
In our models, we use
![]() for the disc outer radius,
z0=0.15 for the disc semi-thickness and
r0=0.05 for the softening (stellar) radius.
The disc aspect ratio is
for the disc outer radius,
z0=0.15 for the disc semi-thickness and
r0=0.05 for the softening (stellar) radius.
The disc aspect ratio is
![]() .
Note that r0=0.05 corresponds
to
.
Note that r0=0.05 corresponds
to
![]() ,
i.e. one solar radius.
Therefore, we shall not reduce it much below this physically meaningful value.
Note, however, that smaller values of r0 would result in faster
outflows (Ouyed & Pudritz 1999).
,
i.e. one solar radius.
Therefore, we shall not reduce it much below this physically meaningful value.
Note, however, that smaller values of r0 would result in faster
outflows (Ouyed & Pudritz 1999).
Furthermore,
![]() and
and
![]() .
We vary the value of
.
We vary the value of
![]() between 0.003 and 0.007.
between 0.003 and 0.007.
The mean-field dynamo is characterized by the parameters
![]() ,
,
![]() ,
,
![]() and
and
![]() .
The total magnetic diffusivity in the disc is therefore
.
The total magnetic diffusivity in the disc is therefore
![]() .
In terms of the usual Shakura-Sunyaev viscosity parameter,
this corresponds to
.
In terms of the usual Shakura-Sunyaev viscosity parameter,
this corresponds to
In terms of the usual nondimensional dynamo parameters we have
| (31) |
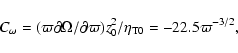 |
(32) |
We take
![]() ,
,
![]() ,
and consider two values of
,
and consider two values of
![]() .
For
.
For
![]() ,
the mass sink at the central object
is suppressed, whereas
,
the mass sink at the central object
is suppressed, whereas
![]() implies instantaneous
accretion of any extra matter (relative to the hydrostatic equilibrium)
by the central object. A realistic
lower limit for
implies instantaneous
accretion of any extra matter (relative to the hydrostatic equilibrium)
by the central object. A realistic
lower limit for
![]() can be estimated
as
can be estimated
as
![]() ,
where
,
where
![]() is the free fall
velocity (given by
is the free fall
velocity (given by
![]() in dimensional quantities).
In most cases we used
in dimensional quantities).
In most cases we used
![]() ,
but we also tried an even smaller value of
,
but we also tried an even smaller value of
![]() and obtained very similar results.
A finite value of
and obtained very similar results.
A finite value of
![]() implies that matter is not
instantaneously absorbed by the sink. Therefore, some matter can leave
the sink if it moves so fast that its residence time in the sink
is shorter than
implies that matter is not
instantaneously absorbed by the sink. Therefore, some matter can leave
the sink if it moves so fast that its residence time in the sink
is shorter than
![]() .
As can be seen below, a small (negligible)
fraction of mass does indeed escape from the sink.
.
As can be seen below, a small (negligible)
fraction of mass does indeed escape from the sink.
Computations have been carried out in domains ranging from
![]() to
to
![]() ,
but
the results are hardly different
in the overlapping parts of the domains.
In our standard computational box,
,
but
the results are hardly different
in the overlapping parts of the domains.
In our standard computational box,
![]() and in the case of the larger computational domain
and in the case of the larger computational domain
![]() .
.
We use third order Runge-Kutta time-stepping and a sixth order finite-difference scheme in space. Details and test calculations are discussed by Brandenburg (2003).
On the outer boundaries, the induction equation is evolved using
one-sided derivatives (open boundary conditions).
The normal velocity component has
zero derivative normal to the boundary, but the velocity
is required to be always directed outwards.
The tangential velocity
components and potential enthalpy on the boundaries are similarly obtained
from the next two interior points away from the boundary.
Tests show that the presence of the boundaries does not affect the flow
inside the computational domain. Regularity
conditions are adopted on the axis where
the ![]() and
and ![]() components of vectorial quantities vanish,
whereas scalar variables and the z components of vectorial quantities
have vanishing radial derivative.
components of vectorial quantities vanish,
whereas scalar variables and the z components of vectorial quantities
have vanishing radial derivative.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{AA9940f3.eps}
\end{figure}](/articles/aa/full/2003/06/aa9940/Timg243.gif) |
Figure 3:
As in Fig. 2, but
with a mass sink at the centre,
|
Copyright ESO 2003