

Up: A study of coronal binaries
Subsections
4 Discussion
In this section, we will discuss the results in terms of a FIP-biased
abundance pattern. We will also discuss potential problems,
such as the relevance of optical depths, and the importance of the choice of
solar and stellar photospheric abundances, that could influence the determination
of coronal abundances or the abundance pattern.
4.1 A pattern for coronal abundances
Figure 4 shows elemental abundance ratios relative to O and
to solar photospheric values for our star sample as a function of the first
ionization potential. Although the determination of absolute abundances
(relative to H) is subject to an accurate description of the underlying
continuum, we have found that abundance ratios are robust and similar in
the XSPEC and SPEX fits. Highly active stars show an inverse FIP effect, i.e.,
low-FIP elements are underabundant relative to high-FIP elements, as observed in
an early analysis of the XMM-Newton RGS data of HR 1099
(Brinkman et al. 2001). 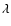 And however shows no particular FIP bias.
For the intermediately active Capella, no clear trend is seen,
although a possible overabundance of low-FIP elements compared to high-FIP
elements is suggested, which is reminiscent of the solar FIP effect. Figure 4
therefore suggests the presence of a transition from an inverse FIP effect in
the most active binaries toward the absence of FIP bias in intermediately active
stars. This resembles the transition from an inverse FIP to a normal FIP effect
in solar-like stars as a consequence of decreasing activity (Güdel et al. 2002).
Similarly, Singh et al. (1999) have observed that the Fe abundance in active late-type
dwarfs increases with decreasing activity.
And however shows no particular FIP bias.
For the intermediately active Capella, no clear trend is seen,
although a possible overabundance of low-FIP elements compared to high-FIP
elements is suggested, which is reminiscent of the solar FIP effect. Figure 4
therefore suggests the presence of a transition from an inverse FIP effect in
the most active binaries toward the absence of FIP bias in intermediately active
stars. This resembles the transition from an inverse FIP to a normal FIP effect
in solar-like stars as a consequence of decreasing activity (Güdel et al. 2002).
Similarly, Singh et al. (1999) have observed that the Fe abundance in active late-type
dwarfs increases with decreasing activity.
![\begin{figure}
\par\resizebox{\hsize}{!}{%
\includegraphics[width=17cm]{MS3099f4.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg36.gif) |
Figure 4:
Abundance ratios relative to O and to solar photospheric values
(Anders & Grevesse 1989) as a function of FIP. Ratios from XSPEC/APEC are shown as
triangles, while ratios from SPEX/MEKAL are shown as squares.
Activity/temperature decreases from top to bottom. Note the logarithmic scales. |
4.2 Optical depths
Optical depths in stellar coronae can potentially have an impact on the determination
of abundances. Since we interpret our data with optically thin models, we
need to verify that the most critical lines seen in our spectra are indeed
optically thin.
We have therefore measured the fluxes in the Fe XVII
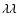 15.014 and
15.261 Å lines. The ratio of these 2p6-2s2p53d lines
is especially sensitive to
the optical depth, since the former line has a very large oscillator
strength, whereas the latter line does not (e.g., Rugge & McKenzie 1985; Mewe et al. 1995b; Kaastra & Mewe 1995).
We used the best-fit models from XSPEC/APEC, then froze the fitting parameters,
set the Fe and O abundances to zero, and added 6 emission lines. This procedure
conserves the
complete model including spectral lines and continuum from all elements except
Fe and O, which we re-model separately to obtain explicit, accurately measured fluxes
specifically for any one of the selected lines. The line photon fluxes
were left free to vary, whereas their widths and their wavelengths were kept fixed.
The additional four emission lines correspond to line blends from Fe XVII
15.014 and
15.261 Å lines. The ratio of these 2p6-2s2p53d lines
is especially sensitive to
the optical depth, since the former line has a very large oscillator
strength, whereas the latter line does not (e.g., Rugge & McKenzie 1985; Mewe et al. 1995b; Kaastra & Mewe 1995).
We used the best-fit models from XSPEC/APEC, then froze the fitting parameters,
set the Fe and O abundances to zero, and added 6 emission lines. This procedure
conserves the
complete model including spectral lines and continuum from all elements except
Fe and O, which we re-model separately to obtain explicit, accurately measured fluxes
specifically for any one of the selected lines. The line photon fluxes
were left free to vary, whereas their widths and their wavelengths were kept fixed.
The additional four emission lines correspond to line blends from Fe XVII 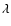 15.453 Å, Fe XIX
15.453 Å, Fe XIX
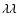 15.079 and 15.198 Å, and O VIII Ly
15.079 and 15.198 Å, and O VIII Ly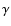 at
15.176 Å. The RGS1 and RGS2 data have been fitted in the wavelength range from 14.8 to 15.5 Å simultaneously to increase the signal-to-noise ratio. Uncertainties for the line photon fluxes were
obtained by averaging the 68% upper and lower limits for a single parameter of
interest (
at
15.176 Å. The RGS1 and RGS2 data have been fitted in the wavelength range from 14.8 to 15.5 Å simultaneously to increase the signal-to-noise ratio. Uncertainties for the line photon fluxes were
obtained by averaging the 68% upper and lower limits for a single parameter of
interest (
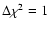 ). The observed flux ratios,
F(15.01) / F(15.26),
range from 2.4 to 3.1 (Table 5).
Theoretical ratios range from 3.0-4.7 (e.g., Bhatia & Doschek 1992; also see Table 2 of Brown et al. 1998).
Laboratory experiments, e.g., with
electron beam ion traps (EBIT) have obtained lower ratios (2.8-3.2, Brown et al. 1998; Laming et al. 2000),
suggesting that previous optical depths measurements based on theoretical
ratios were overestimated. Using an EBIT ratio of
). The observed flux ratios,
F(15.01) / F(15.26),
range from 2.4 to 3.1 (Table 5).
Theoretical ratios range from 3.0-4.7 (e.g., Bhatia & Doschek 1992; also see Table 2 of Brown et al. 1998).
Laboratory experiments, e.g., with
electron beam ion traps (EBIT) have obtained lower ratios (2.8-3.2, Brown et al. 1998; Laming et al. 2000),
suggesting that previous optical depths measurements based on theoretical
ratios were overestimated. Using an EBIT ratio of
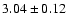 measured at an electron energy of 1150 eV (Brown et al. 1998), and on the basis
of the "escape-factor'' model (escape probability
measured at an electron energy of 1150 eV (Brown et al. 1998), and on the basis
of the "escape-factor'' model (escape probability
![$P(\tau) \sim [1 +
0.43 \tau ]^{-1}$](/articles/aa/full/2003/06/aa3099/img56.gif) for an optical depth
for an optical depth
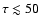 )
with a homogeneous mixture of
emitters and absorbers in a slab geometry (Kaastra & Mewe 1995), we obtain optical depths
no larger than
)
with a homogeneous mixture of
emitters and absorbers in a slab geometry (Kaastra & Mewe 1995), we obtain optical depths
no larger than
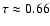 ,
consistent with an optically thin plasma.
Using the theoretical ratio of 3.53 from the APEC code, optical
depths in
,
consistent with an optically thin plasma.
Using the theoretical ratio of 3.53 from the APEC code, optical
depths in 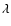 And and possibly Capella approach
And and possibly Capella approach 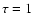 ,
although the
other RS CVns still show
,
although the
other RS CVns still show
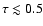 .
.
4.3 Relation to solar photospheric abundances
![\begin{figure}
\par\resizebox{\hsize}{!}{%
\includegraphics[width=17cm]{MS3099f5.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg61.gif) |
Figure 5:
Similar to Fig. 4 for XSPEC/APEC, but using C, N,
O, Ne, Mg, and Fe abundance of Holweger (2001, filled dots) and the C
and O abundances of Allende Prieto et al. (2001, 2002, open squares). |
Solar photospheric abundances from Anders & Grevesse (1989) have been chosen except for
Fe for which the more recent
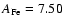 of Grevesse & Sauval (1999) has been
adopted. Recent work has provided new estimates of solar photospheric abundances
(e.g., Grevesse & Sauval 1998; Allende Prieto et al. 2001, 2002; Holweger 2001). In this section, we test
the impact of choosing different solar photospheric abundances on the abundance
pattern in RS CVn binaries; XSPEC/APEC results have been used. However, we emphasize that
the SPEX/MEKAL abundance ratios were similar. Using new abundances from
Holweger (2001), the observed trend (Fig. 4) is again found
(albeit with slightly different ratios). Allende Prieto et al. (2001, 2002) propose
new solar photospheric O and C abundances, respectively:
of Grevesse & Sauval (1999) has been
adopted. Recent work has provided new estimates of solar photospheric abundances
(e.g., Grevesse & Sauval 1998; Allende Prieto et al. 2001, 2002; Holweger 2001). In this section, we test
the impact of choosing different solar photospheric abundances on the abundance
pattern in RS CVn binaries; XSPEC/APEC results have been used. However, we emphasize that
the SPEX/MEKAL abundance ratios were similar. Using new abundances from
Holweger (2001), the observed trend (Fig. 4) is again found
(albeit with slightly different ratios). Allende Prieto et al. (2001, 2002) propose
new solar photospheric O and C abundances, respectively:
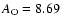 and
and
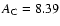 ,
thus factors 1.74 and 1.48 smaller than in Anders & Grevesse (1989). The
result is that abundance ratios to O in Fig. 4 should be reduced
and get closer to the solar photospheric values for high-FIP elements. Although
newer values of solar photospheric abundances can be useful for a direct comparison with the solar
FIP effect, their adoption does not affect the suggested FIP bias in active
stars. Figure 5 is similar to Fig. 4, except that
it shows abundance ratios using Holweger (2001) abundances for C, N, O, Ne,
Mg, Fe (filled dots), and using the C and O abundances of Allende Prieto et al. (2001, 2002, open
squares). We note a possible two-plateau shape, as
for the solar FIP effect but reversed: high-FIP abundance ratios are close to
solar, whereas low-FIP ratios vary with the activity level. The
separation lies around 10 eV, as in the Sun.
,
thus factors 1.74 and 1.48 smaller than in Anders & Grevesse (1989). The
result is that abundance ratios to O in Fig. 4 should be reduced
and get closer to the solar photospheric values for high-FIP elements. Although
newer values of solar photospheric abundances can be useful for a direct comparison with the solar
FIP effect, their adoption does not affect the suggested FIP bias in active
stars. Figure 5 is similar to Fig. 4, except that
it shows abundance ratios using Holweger (2001) abundances for C, N, O, Ne,
Mg, Fe (filled dots), and using the C and O abundances of Allende Prieto et al. (2001, 2002, open
squares). We note a possible two-plateau shape, as
for the solar FIP effect but reversed: high-FIP abundance ratios are close to
solar, whereas low-FIP ratios vary with the activity level. The
separation lies around 10 eV, as in the Sun.
4.4 Relation to stellar photospheric abundances
Although it is practice to normalize stellar coronal abundances to the
solar photospheric abundances, they should better be normalized to the
stellar photospheric abundances. Some studies
attempted to derive photospheric abundances of active binaries by modeling
high-resolution optical spectra. In particular, RS CVn binaries have often been
found to display large metallic abundance depletion (e.g., Randich et al. 1994).
However, such systems are in general younger than the Sun, and thus nearby
stars should show metallicities close to solar (Rocha-Pinto et al. 2000). For
example, at an age of a few Gyrs, photospheres have [Fe/H]
in the range -0.08 to -0.15 with uncertainties of about 0.12(Rocha-Pinto et al. 2000). The rare measured photospheric abundances
are therefore probably biased by the enhanced chromospheric activity, high
rotation rate, and the presence of spots. Previous abundance measurements
are perhaps also biased by inaccurate determinations of fundamental stellar
parameters, such as gravity and effective temperatures (Ottmann et al. 1998).
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[width=17cm]{MS3099f6.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg65.gif) |
Figure 6:
Abundance ratios to oxygen vs. FIP for 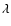 And using the
XSPEC/APEC results. Stellar photospheric
abundances from Donati et al. (1995, red open diamonds) and from
Savanov & Berdyugina (1994, blue open squares) have been used. For comparison, we
plot the ratios to solar photospheric values
(Anders & Grevesse 1989; Grevesse & Sauval 1999, filled circles).
And using the
XSPEC/APEC results. Stellar photospheric
abundances from Donati et al. (1995, red open diamonds) and from
Savanov & Berdyugina (1994, blue open squares) have been used. For comparison, we
plot the ratios to solar photospheric values
(Anders & Grevesse 1989; Grevesse & Sauval 1999, filled circles). |
On the other hand, photospheric abundances of 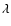 And, a slowly rotating
giant, can be found in the literature. We have used abundances from
Donati et al. (1995)
And, a slowly rotating
giant, can be found in the literature. We have used abundances from
Donati et al. (1995)![[*]](/icons/foot_motif.gif) and
Savanov & Berdyugina (1994)
and
Savanov & Berdyugina (1994)![[*]](/icons/foot_motif.gif) since these authors
provide estimates for several elements. Note that Ottmann et al. (1998) give
values for Fe, Mg, and Si only, all of which are low-FIP elements with very
similar FIP values. Figure 6 shows FIP-ordered abundance ratios
to oxygen relative to stellar photospheric abundances (red open
diamonds for Donati et al. 1995 and blue open squares for Savanov & Berdyugina 1994)
in comparison with ratios relative to solar photospheric. Abundance ratios are
slightly different, the overall shape of the coronal abundance pattern in
since these authors
provide estimates for several elements. Note that Ottmann et al. (1998) give
values for Fe, Mg, and Si only, all of which are low-FIP elements with very
similar FIP values. Figure 6 shows FIP-ordered abundance ratios
to oxygen relative to stellar photospheric abundances (red open
diamonds for Donati et al. 1995 and blue open squares for Savanov & Berdyugina 1994)
in comparison with ratios relative to solar photospheric. Abundance ratios are
slightly different, the overall shape of the coronal abundance pattern in
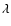 And stays similar, however: there is no apparent bias related to the
first ionization potential. The Ca/O ratio using stellar abundances of
Donati et al. (1995) is similar to the ratio relative to solar photospheric, but it
is larger when abundances from Savanov & Berdyugina (1994) are used, although with larger
uncertainties, thus formally compatible. Unfortunately, abundances of noble
gases in stellar photospheres cannot be measured, preventing us from obtaining
abundance ratios at
And stays similar, however: there is no apparent bias related to the
first ionization potential. The Ca/O ratio using stellar abundances of
Donati et al. (1995) is similar to the ratio relative to solar photospheric, but it
is larger when abundances from Savanov & Berdyugina (1994) are used, although with larger
uncertainties, thus formally compatible. Unfortunately, abundances of noble
gases in stellar photospheres cannot be measured, preventing us from obtaining
abundance ratios at
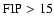 eV.
eV.
 And may be regarded as an exceptional case where stellar photospheric
abundances have been measured with some confidence. It would be interesting to
obtain measurements for highly active stars, such as UX Ari and
HR 1099, for which a clear inverse FIP effect is observed. However, abundance
determinations are rare or often unclear (e.g., for the X-ray bright K star in
HR 1099,
And may be regarded as an exceptional case where stellar photospheric
abundances have been measured with some confidence. It would be interesting to
obtain measurements for highly active stars, such as UX Ari and
HR 1099, for which a clear inverse FIP effect is observed. However, abundance
determinations are rare or often unclear (e.g., for the X-ray bright K star in
HR 1099,
![${\rm [Fe/H]} = 0$](/articles/aa/full/2003/06/aa3099/img74.gif) from Savanov & Tuominen 1991
but
from Savanov & Tuominen 1991
but
![${\rm [Fe/H]} \approx -0.6$](/articles/aa/full/2003/06/aa3099/img75.gif) for Randich et al. 1994; these authors used
solar abundances from Anders & Grevesse 1989, thus a correction of +0.17 dex must
be introduced for the Fe abundance).
for Randich et al. 1994; these authors used
solar abundances from Anders & Grevesse 1989, thus a correction of +0.17 dex must
be introduced for the Fe abundance).
4.5 Coronal abundances in stars
RS CVn binaries show enhanced magnetic activity thought to arise from the tidal
interaction with their companions. Intermediately active binaries often
correspond to loosely bound stars. Our sample thus investigates the upper range
of coronal activity. In contrast, the solar-like stars sampled by
Güdel et al. (2002) span all activity levels. Assuming that abundance ratios
relative to solar photospheric in our sample approximately correspond to ratios
relative to stellar photospheric abundances, we have compared the correlation between
the FIP bias and the coronal activity, here characterized by the average coronal
temperature, in RS CVn binaries and in solar analogs (Fig. 7).
The average coronal temperature for the solar analogs were obtained with
the same procedure as in Sect. 3.3. They are
similar to those derived in previous studies, e.g., Güdel et al. (1997).
Low-FIP abundance ratios (here exemplified by Fe) vary dramatically with the
coronal temperature, whereas high-FIP abundance ratios (exemplified by Ne) show
no variation. Note that ratios relative to Fe naturally show the inverse trend
(low-FIP ratios constant, high-FIP ratios increasing with temperature). Together
with the apparent increase of the absolute Fe abundance with decreasing
activity level in RS CVn binaries, this suggests that abundances of elements
with low first ionization potential vary with magnetic activity, whereas those of
elements with high FIP stay constant.
![\begin{figure}
\par\resizebox{\hsize}{!}{ \includegraphics[width=17cm]{MS3099f7.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg76.gif) |
Figure 7:
Fe/O and Ne/O abundance ratios relative to solar photospheric values
(Anders & Grevesse 1989; Grevesse & Sauval 1999) for RS CVn and solar analogs
using the XSPEC/APEC results (the SPEX/MEKAL results give similar
relations) as a function of the average coronal
temperature. Low-FIP abundance ratios follow an anticorrelation with
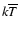 ,
whereas high-FIP elements show no correlation. ,
whereas high-FIP elements show no correlation. |


Up: A study of coronal binaries
Copyright ESO 2003
![\begin{figure}
\par\resizebox{\hsize}{!}{%
\includegraphics[width=17cm]{MS3099f4.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg36.gif)
![\begin{figure}
\par\resizebox{\hsize}{!}{%
\includegraphics[width=17cm]{MS3099f5.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg61.gif)
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[width=17cm]{MS3099f6.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg65.gif)
![\begin{figure}
\par\resizebox{\hsize}{!}{ \includegraphics[width=17cm]{MS3099f7.eps}} \end{figure}](/articles/aa/full/2003/06/aa3099/Timg76.gif)