3 High-resolution X-ray spectra

We have interpreted the EPIC and RGS spectra using collisional ionization equilibrium (CIE) plasma models with variable cosmic abundances. To obtain reasonable estimates taking into account the uncertainties in the atomic parameters, we have used two different software packages that contain different atomic databases. The Utrecht software SPEX (Kaastra et al. 1996) uses an updated version of the MEKAL spectral code (Mewe et al. 1985; Mewe et al. 1995a; Phillips et al. 1999) with ionization balances from Arnaud & Rothenflug (1985) and Arnaud & Raymond (1992) for Fe. The XSPEC 11.0.1aj (Arnaud 1996) software uses the APEC 1.0.1 spectral code (Smith et al. 2001) with the self-consistent ionization balance from Mazzotta et al. (1998). The RGS spectra were grouped with a minimum of 30 to 80 counts per bin (depending on the source), whereas the EPIC MOS2 data were binned with a minimum of 25 counts per bin (100 for HR 1099).

  
3.1 Analysis approach

X-ray spectra have conventionally been interpreted either by measuring a number of selected lines above the continuum level and subsequently reconstructing the emission measure distribution and the abundances; or by fitting complete thermal models to the total spectrum. Each approach encounters severe limitations with our data. Extracting single line fluxes from RGS spectra is difficult in particular in the crucial but crowded region between 10-20 Å because of line blends and strongly overlapping line profiles and extended line wings. On the other hand, fits of the complete spectrum with pre-calculated thermal models are affected by numerous emission lines with poor atomic physics parameters in the codes (e.g., Audard et al. 2001b; Laming 2002; Raassen et al. 2002). We have chosen to apply a method half-way between the above two extremes that is ideally suited for RGS spectra. We selected a restricted number of individual, bright lines that are believed to be well known in the spectral codes and that cover a wide range of elements and ionization stages. Pieces of most likely line-free regions have been included for an accurate determination of the continuum level. By modeling the lines together and using the calibrated line spread function, we obtain an optimum determination of the fluxes of all overlapping lines. Since we still use a full thermal model including all catalogued lines and the continuum falling within the considered pieces of the spectrum, the method simultaneously takes care of possible ill-recognized weaker lines that may add a pseudo-continuum or that may blend with the selected line, thus altering their fluxes. Our method thus tries to maximize the information extraction from individual lines, and at the same time it approximately models additional flux contributions by weak lines in a self-consistent way.

The high signal-to-noise ratios of the spectra of our RS CVn binaries display a well-developed continuum emission, allowing us to put constraints on the EM from regions free of emission lines. The RGS and EPIC MOS2 spectra were interpreted simultaneously, with the exception of Capella (RGS only). We have introduced a free constant model to multiply the physical model for EPIC. This factor takes into account cross-calibration inaccuracies and especially corrects for the finite extraction radius used to obtain the source spectra. Indeed, the EPIC responses had been built under the assumption of an infinite extraction radius, hence overestimating the effective area. Note that the XMM-Newton on-axis PSF for the MOS cameras are almost energy-independent (Ehle et al. 2001); our 50 $^{\prime\prime}$ extraction regions include $\approx$90% of the fractional encircled energy. The best-fit values for the constant ranged between 0.90-0.95, except for HR 1099 (0.23-0.25) because we removed the central part of the PSF. To profit from the higher spectral resolution of the RGS, we have discarded the EPIC wavelength range longward of the Mg IX He$\alpha$ triplet ( $\lambda \ge 9.35$ Å, $E \le 1.33$ keV). Similarly, we eliminated the RGS wavelength range shortward of the Mg X Ly$\alpha$ line ( $\lambda \le 8.3$ Å, $E \ge 1.49$ keV) because of the small RGS effective area at high energies and the consequent limited quality of the calibration - with the exception of Capella, for which we included the range from 6.5 to 6.8 Å to account for the bright Si He-like triplet. Therefore, the RGS and EPIC spectra overlap around the Mg lines. The consistency between the two detector systems is additionally provided by the cross calibration, and by the broad-band continuum in both spectra.

Figure 1: RGS first order spectra of the observed targets. The size of the wavelength bin is 25 mÅ. The spectra are ordered approximately with decreasing coronal activity (defined in this paper as the average coronal temperature) from top to bottom.

 

 

Table 3: Spectral wavelength ranges excluded from the fitting procedure. Note that RGS stands for both RGS1 and RGS2.

Instrument	$\lambda$ range (Å)
RGS ............................................	$\leq$8.3a
RGS ............................................	9.50-12.00
RGS ............................................	13.95-14.15
RGS ............................................	15.90-16.20
RGS ............................................	17.15-17.80
RGS ............................................	18.30-18.75
RGS ............................................	19.20-20.80
RGS ............................................	21.10-21.40
RGS1 ..........................................	$\geq$22.40
RGS2 ..........................................	22.40-23.65
RGS2 ..........................................	24.00-24.50
RGS2 ..........................................	24.90-28.50
RGS2 ..........................................	30.10-31.10
RGS2 ..........................................	32.00-33.40
RGS2 ..........................................	$\geq$33.85
MOS2 ..........................................	$\leq$1.00
MOS2 ..........................................	6.80-7.80
MOS2 ..........................................	$\geq$9.35
a For Capella, we included the range 6.5-6.8 Å.

The physical model was defined as a photoelectric absorption component with free atomic H column density (only for RGS1 and RGS2), and a combination of CIE models with free temperature, EM, and abundances (C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, Ni). In practice, a 4-T model proved adequate to fit the spectra, except for Capella for which a 3-T model was sufficient. The absorption components were left free to vary between RGS1 and RGS2 to account for cross-calibration uncertainties between the two instruments at the long wavelength end. The interstellar absorption is negligible for these nearby sources in the wavelength range of the RGS. Note that we have included an absorption edge model at 23.3 Å that was not yet included in the RGS effective areas generated by XMM-Newton SAS 5.2 (see, e.g., den Herder et al. 2002).

Figure 2: Extract of EPIC MOS2 spectra from 1 to 10 keV. The spectra have been shifted logarithmically along the vertical axis, for clarity (see labels). Some H-like and He-like transitions are indicated.

  
3.2 Exclusion of lines with inaccurate atomic data

For this paper, we have decided to systematically exclude RGS spectral ranges where L-shell lines dominate (except those of Fe and Ni) because these lines are often inaccurately described in present spectral codes (Audard et al. 2001b). Eventually, most of the long wavelength range of the RGS spectra was eliminated. There remain however still some relatively bright low-Z L-shell lines in Capella's spectrum that we used to obtain the Si, S, Ar, and Ca abundances. These lines have atomic parameter uncertainties in the range 10-50%. The results, in particular for S, Ar, and Ca for Capella should therefore be treated with some caution. The Si He-like triplet was also included for this star; we caution, however, that the calibration of the effective area in this range is less reliable. A few Fe lines were discarded as well (e.g., Fe XVIII $\lambda$ 16.0 Å, Fe lines in the 9.5-12.0 Å range) as they were poorly fitted with both spectral codes. Table 3 summarizes the spectral ranges excluded from the fitting procedure.

  

Table 4: Elemental abundances relative to solar photospheric abundances from Anders & Grevesse (1989) except for Fe for which the solar photospheric value is taken from Grevesse & Sauval (1999). Temperatures are in keV, and EM in cm^-3. Uncertainties refer to 90% confidence ranges for elemental abundances, but they are defined as 10% of the best-fit values for temperatures, and 0.1 dex for the EM (see text).

$$\begin{tabular}{p{2cm}rrrrrrrr} \noalign{\smallskip }\hline\h... ... \noalign{\smallskip }\hline\noalign{\smallskip } \end{tabular}$$

  
3.3 Results

RGS fluxed spectra are shown in Fig. 1 ordered approximately in decreasing coronal activity (defined in this paper as the average coronal temperature - see below). Ne X, O VIII, and Fe L-shell lines dominate the RGS spectra. In contrast to the other RS CVn binaries in our sample, the Capella X-ray spectrum is softer and dominated by bright Fe XVII and Fe XVIII lines as previously observed (e.g., Brinkman et al. 2000; Canizares et al. 2000; Audard et al. 2001b; Behar et al. 2001; Mewe et al. 2001). We provide the high-energy EPIC MOS2 spectra in Fig. 2, except for Capella. The high quality of the spectra allows for the determination of Mg, Si, S, Ar, Ca, and Fe or upper limits thereof. Continuum emission is clearly detected in these bright X-ray sources, which provides constraints for the determination of the emission measure distributions. Although the X-ray spectra look similar (with the exception of Capella), each star shows different strengths of line fluxes and their ratios. For example, the strong N VII Ly$\alpha$line flux in UX Ari contrasts with that in, e.g., $\lambda$ And. However, in the former star, no significant N VI He-like triplet is detected, which points to an EM distribution dominated by high temperatures. Indeed, the formation of the N VI He-like triplet is constrained to a narrow range of (cool) temperatures (1.0-2.5 MK; e.g., Mewe et al. 1985). In contrast, the triplet is detected in Capella's spectrum. Note that the short wavelength range (5-10 Å) for the most active stars HR 1099 and UX Ari show weaker lines compared to the less active $\lambda$ And and Capella. In this range, H-like and He-like lines of Si and Mg should dominate together with transitions from highly ionized Fe. These elements have a low first ionization potential, which suggests that their coronal abundances are low. Also, the coronal temperature could be much lower than the maximum formation temperatures of these emission lines, but this is unlikely since the lines form at $\approx$10 MK, close to the average temperature of these coronae. In contrast, the 5-10 Å range in $\lambda$ And and Capella displays better developed emission lines, suggesting higher abundances of low-FIP elements in these stellar coronae.

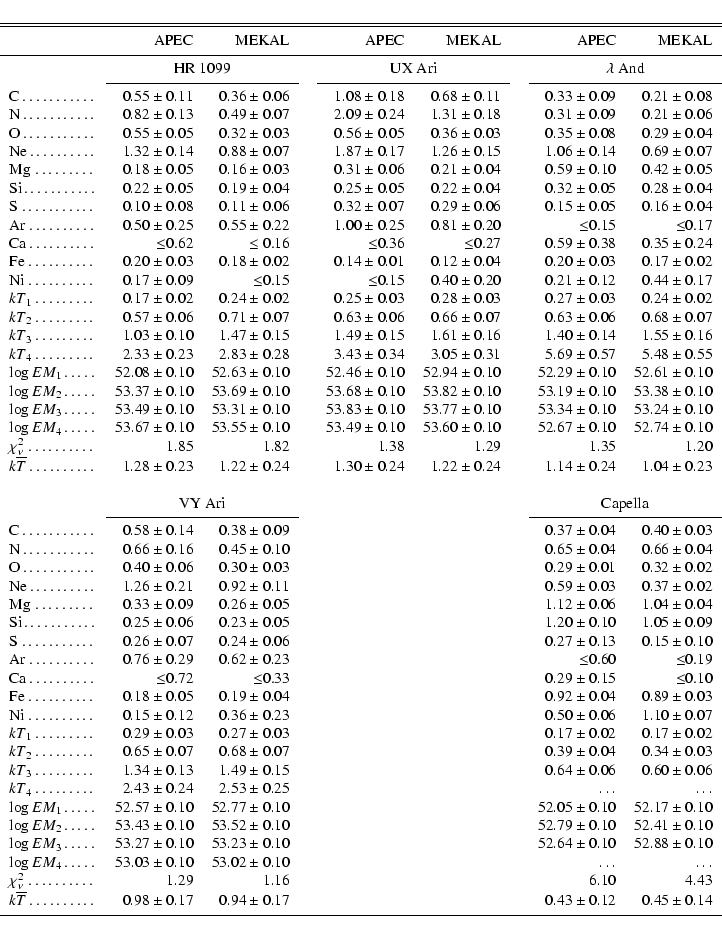
Coronal abundances obtained from the multi-temperature fits in SPEX and XSPEC are summarized in Table 4. As an example, Fig. 3 shows best fits and residuals for UX Ari. We provide reduced $\chi ^2$ values, although we emphasize that current uncertainties in the instrument calibration, in the atomic codes, and high signal-to-noise (S/N) ratios can produce systematic errors that cannot be described by $\chi ^2$. This is especially the case for Capella, for which its high S/N ratio produces $\chi ^2$ values exceeding 4. Inspection of the fit by eye shows, however, good agreement between the model fit and the data. The deviations are smaller than the typical uncertainties on the atomic physics parameters (order of 10%). Given the current uncertainties in the atomic parameters, our model description is thus satisfactory. Statistical 90% confidence ranges are given for each elemental abundance in Table 4. Since EM distributions are continuous, a 4-T model only provides an approximate discrete representation. Formal errors for T and EM are artificially underestimated, and are therefore of little use in this context. We adopt conservative estimates of the uncertainties for T as 10% of their values, whereas EM uncertainties are estimated to 0.1 dex. To characterize the global temperature average of the stellar corona, we hereafter assign an "average'' coronal temperature to each star (given in Table 4), obtained from the sum of logarithmic temperatures weighted by their EM,

$$\log \overline{T} = \frac{\sum_{i=1}^{N} \log T_i \times EM_i}{\sum_{i=1}^{N} EM_i}\cdot$$ (1)

The error of the average temperature is obtained as

 

$$\Delta ( \log \overline{T} ) \sqrt{\frac{1}{N}\frac{\sum_{i=1}^{N} EM_i \times (\log T_i - \log \overline{T} )^2}% {(N - 1) \sum_{i=1}^{N} EM_i}},$$ = (2)

$$\Delta ( \overline{T} ) \sqrt{(\overline{T}_+ - \overline{T}) \times (\overline{T} - \overline{T}_-)},$$ = (3)

where

$$\overline{T}_+ 10^{\log \overline{T} + \Delta ( \log \overline{T} )},$$ = (4)

$$\overline{T}_- 10^{\log \overline{T} - \Delta ( \log \overline{T} )}.$$ = (5)

Such procedure has been applied to the XSPEC/APEC and SPEX/MEKAL results. For our subsequent discussion and the figures, we will use the derived coronal abundances and average coronal temperature from both spectral codes separately.

Figure 3: EPIC MOS2 (blue), RGS1 (red), and RGS2 (green) data of UX Ari with the 4-T best fits overlaid (thick black) for XSPEC/APEC (upper panel) and SPEX/MEKAL (lower panel). Error bars are plotted for MOS only, for clarity. Contributions to the $\chi ^2$ are also plotted; if the data bin is above the model, the $\chi ^2$ contribution is positive. Zoom-ins from 13 Å to 20 Å show the quality of the fits in the region from the Ne IX He-like triplet to O VIII Ly$\alpha$ and include bright Fe XVII and Fe XVIII lines. The wavelength ranges used for the fits (Table 3) are shown by horizontal bars for each instrument.