The content of an image is often complex, and there is not a single
transform which is optimal to represent all the contained features. For
example, the Fourier transform better represents some textures, while
the wavelet transform better represents singularities. Even if we limit
our class of transforms to the wavelet one, decision have to
be taken between an isotropic wavelet transform which produce good
results for isotropic objects (such stars and galaxies in astronomical
images, cells in biological images, etc.), or an orthogonal wavelet
transform, which is better for images with edges.
This has motivated
the development of different methods (Chen et al. 1998; Meyer et al. 1998; Huo 1999),
and the two most frequently discussed approaches are the Matching Pursuit (MP)
(Mallat & Zhang 1993) and the Basis pursuit (BP) (Chen et al. 1998).
A dictionary ![]() being defined as a collection of waveforms
being defined as a collection of waveforms
![]() ,
the general principe consists in representing a signal s as a "sparse''
linear combination of a small number of basis such that:
,
the general principe consists in representing a signal s as a "sparse''
linear combination of a small number of basis such that:
| (11) |
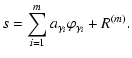 |
(12) |
| Rk+1 = s - sk . | (13) |
Basis pursuit method (Chen et al. 1998) (BP) is a global procedure which
synthesizes an approximation ![]() to s by minimizing a
functional of the type
to s by minimizing a
functional of the type
In many cases, BP or MP synthesis algorithms are computationally very expensive. We present in the following an alternative approach, that we call Combined Transforms Method (CTM), which combines the different available transforms in order to benefit of the advantages of each of them.
Depending on the content of the data, several transforms can be combined in order to get an optimal representation of all features contained in our data set. In addition to the ridgelet and the curvelet transform, we may want to use the à trous algorithm which is very well suited to astronomical data, or the undecimated wavelet transform which is commonly used in the signal processing domain.
Other transform such wavelet packets, the Fourier transform, the Pyramidal median transform (Starck et al. 1998), or other multiscale morphological transforms, could also be considered. However, we found that in practice, these four transforms (i.e. curvelet, ridgelet, à trous algorithm, and undecimated wavelet transform) furnishes a very large panel of waveforms which is generally large enough to well represents all features contained in the data.
In general, suppose that we are given K linear transforms
![]() and let
and let ![]() be the coefficient sequence of an
object x after applying the transform Tk, i.e.
be the coefficient sequence of an
object x after applying the transform Tk, i.e.
![]() .
We will suppose that for each transform Tk we have available a
reconstruction rule that we will denote by T-1k although this is
clearly an abuse of notations.
.
We will suppose that for each transform Tk we have available a
reconstruction rule that we will denote by T-1k although this is
clearly an abuse of notations.
Therefore, we search a vector
![]() such that
such that
| (15) |
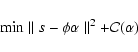 |
(16) |
Two iterative methods, soft-CTM and hard-CTM, allowing us to realize such a combined transform, are described in this section.
![\begin{figure}
\par {\hspace*{3.75cm}\includegraphics[width=6.5cm,clip]{fig_cb2_...
...pace*{1mm}
\includegraphics[width=6.5cm,clip]{fig_cb2_line_g_rid.ps}\end{figure}](/articles/aa/full/2003/05/aa2574/Timg111.gif) |
Figure 10: Top, original image containing lines and gaussians. Botton left, reconstructed image for the à trous wavelet coefficient, bottom right, reconstructed image from the ridgelet coefficients. |
Noting
T1, ..., TK the K transform operators,
a solution
![]() is obtained by minimizing a functional of the form:
is obtained by minimizing a functional of the form:
An simple algorithm to achieve such an solution is:
In some specific cases where the data are sparse in all bases,
it has been shown (Huo 1999; Donoho & Huo 2001)
that the solution is identical to the solution when using a
![]() penalty term. This is however generally not the
case.
The problem we met in image restoration applications,
when minimizing Eq. (17), is
that both the signal and noise are split into the bases. The way the noise
is distributed in the coefficients
penalty term. This is however generally not the
case.
The problem we met in image restoration applications,
when minimizing Eq. (17), is
that both the signal and noise are split into the bases. The way the noise
is distributed in the coefficients ![]() is not known, and leads to the problem
that we do not know at which level we should threshold the coefficients. Using
the threshold we would have used with a single transform
makes a strong over-filtering of the data. Using the l1 optimization
for data restoration implies to first study how the noise is
distributed in the coefficients. The hard-CTM method does not present
this drawback.
is not known, and leads to the problem
that we do not know at which level we should threshold the coefficients. Using
the threshold we would have used with a single transform
makes a strong over-filtering of the data. Using the l1 optimization
for data restoration implies to first study how the noise is
distributed in the coefficients. The hard-CTM method does not present
this drawback.
The following algorithm consists in hard thresholding the residual successively on the different bases.
It seems that starting with a high enough ![]() and a high
number of iterations would lead to the l0 optimization solution,
but this remains to be proved.
and a high
number of iterations would lead to the l0 optimization solution,
but this remains to be proved.
Figure 11 upper left shows
a compact blue galaxy located at 53 Mpc. The data have been
obtained on ground with the GEMINI-OSCIR instrument at 10 ![]() m.
The pixel field of
view is
m.
The pixel field of
view is
![]() /pix, and the source was observed during 1500s.
The data are contaminated by a noise and a stripping artifact due to the
instrument electronic. The same kind of artifact pattern were observed with
the ISOCAM instrument (Starck et al. 1999).
/pix, and the source was observed during 1500s.
The data are contaminated by a noise and a stripping artifact due to the
instrument electronic. The same kind of artifact pattern were observed with
the ISOCAM instrument (Starck et al. 1999).
This image, noted D10, has been decomposed using wavelets, ridgelets, and curvelets. Figure 11 upper middle, upper right, and bottom left show the three images R10, C10, W10reconstructed respectively from the ridgelets, the curvelets, and the wavelets. Image in Fig. 11 bottom middle shows the residual, i.e. e10 = D10 - (R10 + C10 + W10). Another interesting image is the artifact free one, obtained by subtracting R10 and C10 from the input data (see Fig. 11 bottom right). The galaxy has well been detected in the wavelet space, while all stripping artifact have been capted by the ridgelets and curvelets.
Figure 12 upper left shows the same galaxy, but at
20 ![]() m. We have applied the same decomposition on D20.
Figure 12 upper right shows the coadded
image
R20 + C20, and we can see bottom left and right the
wavelet reconstruction W20 and the residudal
e20 = D20 - (R20 + C20 + W20).
m. We have applied the same decomposition on D20.
Figure 12 upper right shows the coadded
image
R20 + C20, and we can see bottom left and right the
wavelet reconstruction W20 and the residudal
e20 = D20 - (R20 + C20 + W20).
Figure 13 upper left shows the HST A370 image. It contains many anisotropic features such the gravitationnal arc, and the arclets. The image has been decomposed using three transforms: the ridgelet transform, the curvelet transform, and the à trous wavelet transform. Three images have then been reconstructed from the coefficients of the three basis. Figure 13 upper right shows the coaddition of the ridgelet and curvelet reconstructed images. The à trous reconstructed image is displayed in Fig. 13 lower left, and the coaddition of the three images can be seen in Fig. 13 lower right. The gravitational arc and the arclets are all represented in the ridgelet and the curvelet basis, while all isotropic features are better represented in the wavelet basis.
Figure 14 shows the result of a decomposition of a spiral galaxy (NGC 2997). This image (Fig. 14 top left) contains many compact structures (stars and HII region), more or less isotropic, and large scale elongated features (NGC 2997 spiral part). Compact objects are well represented by isotropic wavelets, and the elongated features are better represented by a ridgelet basis. In order to benefit of the optimal data representation of both transforms, the image has been decomposed on both the "à trous'' wavelet transform and on the ridgelet transform by using the same method as described in Sect. 5.4. When the functional is minimized, we get two images, and their coaddition is the filtered version of the original image. The reconstructions from the à trous coefficients, and from the ridgelet coefficients can be seen in Fig. 14 top right and bottom left. The addition of both images is presented in Fig. 14 bottom right.
We can see that this Morphological Component Analysis (MGA) allows us to separate automatically features in an image which have different morphological aspects. It is very different from other techniques such as Principal Component Analysis or Independent Component Analysis (Cardoso 1998) where the separation is performed via statistical properties.
Acknowledgements
We are grateful to the referee for helpful comments on an earlier version.
Copyright ESO 2003