The normal way to choose "good'' components of a multi-index quantity
like
![]() is to look for its behavior under
coordinate transformations. Recall the situation for the shear
two-point correlation function: the correlator
is to look for its behavior under
coordinate transformations. Recall the situation for the shear
two-point correlation function: the correlator
![]() of the Cartesian components of the shear contains
two terms, one which is independent on the phase
of the Cartesian components of the shear contains
two terms, one which is independent on the phase ![]() of
of ![]() ,
the
other behaving as
,
the
other behaving as
![]() .
The coefficients of these two terms
are
.
The coefficients of these two terms
are ![]() and
and ![]() ,
respectively, which are the invariants, and
therefore the natural choice for the components of the two-point
correlation function of the shear.
,
respectively, which are the invariants, and
therefore the natural choice for the components of the two-point
correlation function of the shear.
Similarly, we can consider the behavior of the 3PCF under rotations. Given that no linear scalar can be built from the Cartesian components of the 3PCF alone we cannot expect to find a combination of components which is invariant under general rotations. However, as we shall see, there are linear combinations of the components of the 3PCF which have a simple behavior under rotations, namely multiplication by a phase factor. Owing to this simple transformation behavior, we shall term them "natural'' components.
Let now
![]() be the components of the 3PCF of
the shear measured with respect to one particular choice of
direction(s); choosing different projection directions, which differ
from the old ones by
be the components of the 3PCF of
the shear measured with respect to one particular choice of
direction(s); choosing different projection directions, which differ
from the old ones by ![]() ,
the 3PCF becomes
,
the 3PCF becomes
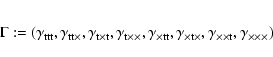
We see that under the general rotation described by
Eq. (16), the eigenvalue +1 does not occur; in other
words, there is no (linear) combination of the components of the 3PCF
that is invariant under the transformation (16). However, for some special rotations, the eigenvalue +1 occurs. As a first example, we consider the case
![]() ;
as shown in Sect. 3.2, this case
actually is encountered for transformations of the shear components
between the orthocenter, the incenter and the circumcenter. Then, the
two eigenvalues
;
as shown in Sect. 3.2, this case
actually is encountered for transformations of the shear components
between the orthocenter, the incenter and the circumcenter. Then, the
two eigenvalues
![]() are +1, and the corresponding
eigenvectors can be found to be
are +1, and the corresponding
eigenvectors can be found to be
| E(0)1 = (1,0,0,-1,0,-1,-1,0); | |||
| E(0)2 = (0, 1, 1, 0, 1, 0, 0, -1). | (18) |
| (19) |
Next we consider the case that
![]() .
Such a
rotation occurs if one transforms the shear components from the
incenter (or the out- or orthocenter) to the center of one of the
escribed circles (see Fig. 6 for an explanation); in this case,
.
Such a
rotation occurs if one transforms the shear components from the
incenter (or the out- or orthocenter) to the center of one of the
escribed circles (see Fig. 6 for an explanation); in this case,
![]() ,
and from the corresponding eigenvectors one
can again construct two combinations
,
and from the corresponding eigenvectors one
can again construct two combinations
![]() ,
,
![]() ,
of the
components of the 3PCF that stay invariant under such a rotation, and
they can as well be combined into a single complex quantity. The same
procedure can then be repeated for rotations with
,
of the
components of the 3PCF that stay invariant under such a rotation, and
they can as well be combined into a single complex quantity. The same
procedure can then be repeated for rotations with
![]() and those with
and those with
![]() ;
these correspond, e.g., to the
transformation from one of the aforementioned centers to the centers
of the other two escribed circles. The corresponding invariants read:
;
these correspond, e.g., to the
transformation from one of the aforementioned centers to the centers
of the other two escribed circles. The corresponding invariants read:
Of course, if desired, the original components of the shear 3PCF can
be obtained from the natural components; the inverse of
Eq. (21) reads:
| (23) |
A parity transformation is obtained by mirroring a given set of three
points with respect to any straight line. Such a transformation has
the following effects: if in the original triangle the three points
![]() ,
,
![]() ,
,
![]() are ordered counterclockwise with
respect to, say, the center of the incircle, in the transformed
triangle they will be ordered clockwise. As a result, under a parity
transformation we need to replace every angle with its opposite.
are ordered counterclockwise with
respect to, say, the center of the incircle, in the transformed
triangle they will be ordered clockwise. As a result, under a parity
transformation we need to replace every angle with its opposite.
In order to understand the behavior of the 3PCF under parity, let us
suppose that the triangle is flipped along a line perpendicular to the
side ![]() (since the 3PCF is invariant upon rotation, the
direction used for the flipping is irrelevant). We first observe that
this mirror symmetry is equivalent to interchanging the points
(since the 3PCF is invariant upon rotation, the
direction used for the flipping is irrelevant). We first observe that
this mirror symmetry is equivalent to interchanging the points ![]() and
and ![]() ,
or the sides x1 and x2. Second, such a
flipping of orientation keeps the tangential component of the shear
invariant (if the direction relative to which the shear components are
measured are as well subject to the mirror transformation - like it
happens when shear components are defined relative to one of the
centers of the triangle), but changes the sign of the cross-component;
hence, this transformation implies
,
or the sides x1 and x2. Second, such a
flipping of orientation keeps the tangential component of the shear
invariant (if the direction relative to which the shear components are
measured are as well subject to the mirror transformation - like it
happens when shear components are defined relative to one of the
centers of the triangle), but changes the sign of the cross-component;
hence, this transformation implies
![]() .
Together, these two effects therefore imply that under a
parity transformation,
.
Together, these two effects therefore imply that under a
parity transformation,
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | |||
| = | (25) |
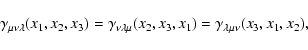 |
(26) |
The parity transformations have an immediate consequence for triangles
where two sides are equal, say x1=x2; namely, from
Eq. (24) one finds that
| (28) |
The foregoing formalism can of course also be applied to the two-point
correlation function. In that case, the eigenvalues are
![]() ,
and the invariant combinations are
,
and the invariant combinations are
![]() and
and
![]() .
The two-point correlator is, however,
special in the sense that after a parity transformation, the two
points can be brought back into the old positions with a
rotation. This then implies that the imaginary components of the
.
The two-point correlator is, however,
special in the sense that after a parity transformation, the two
points can be brought back into the old positions with a
rotation. This then implies that the imaginary components of the
![]() vanish if they are measured in the only reference
frame that makes sense for two points - namely, the line connecting
them; and so
vanish if they are measured in the only reference
frame that makes sense for two points - namely, the line connecting
them; and so
![]() ,
,
![]() .
Note that if different projection directions are taken, the
imaginary parts of the
.
Note that if different projection directions are taken, the
imaginary parts of the
![]() are not zero.
are not zero.
The discussion on obtaining the natural components of the shear 3PCF immediately suggests how to generalize it to the natural components of higher-order correlation functions. Here, we shall give the results for the four-point function (also see the recent work by Takada & Jain 2002a for a detailed consideration of the kurtosis of the cosmic shear field); further generalizations are straightforward to obtain:
If
![]() is the four-point correlation
function of the shear (for notational simplicity, we skip the
arguments of this function), and we consider a general rotation of the
directions relative to which tangential and cross components are
defined, the transformation of the shear four-point correlation
function reads
is the four-point correlation
function of the shear (for notational simplicity, we skip the
arguments of this function), and we consider a general rotation of the
directions relative to which tangential and cross components are
defined, the transformation of the shear four-point correlation
function reads
| (31) |
| |
= | ||
| (32) |
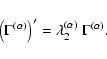 |
(33) |
In their paper, Bernardeau et al. (2002b) considered, for the first
time, a specific shear 3PCF, which they then applied successfully to
observational cosmic shear data (Bernardeau et al. 2002a). Here, we
shall write the Bernardeau et al. (2002b) estimator in our
notation. They considered one side of a triangle (say, ![]() )
as
the reference direction, and project the shear at all three points
along this direction. Hence, their projected components (here written
as
)
as
the reference direction, and project the shear at all three points
along this direction. Hence, their projected components (here written
as
![]() )
read
)
read
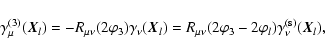 |
(34) |
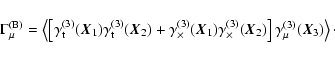 |
(35) |
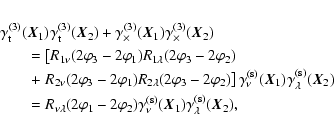
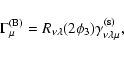 |
(36) |
Copyright ESO 2003