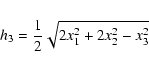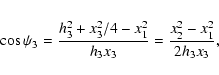Up: The three-point correlation function
Subsections
Consider three points 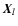 ,
,
 ,
and define their
difference vectors
,
and define their
difference vectors
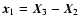 ,
,
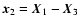 ,
,
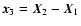 ,
so that
,
so that
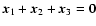 (see Fig. 1). Each of the three difference vectors
will be written as
(see Fig. 1). Each of the three difference vectors
will be written as
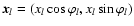 ,
so that
,
so that
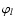 is the orientation of the lth side of the
triangle. Furthermore, we define
is the orientation of the lth side of the
triangle. Furthermore, we define 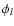 as being the interior angle
of the triangle at the corner
as being the interior angle
of the triangle at the corner 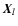 .
In order to have general
relations, in this paper we will use oriented angles, i.e.
we will attach to each angle a sign indicating its orientation. More
precisely, we will define
.
In order to have general
relations, in this paper we will use oriented angles, i.e.
we will attach to each angle a sign indicating its orientation. More
precisely, we will define
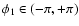 to have the same sign
of the cross product
to have the same sign
of the cross product
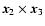 (where
(where
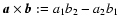 ),
and similarly for
),
and similarly for 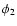 and
and 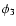 .
Note that, since
.
Note that, since
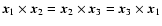 (which follows from the vanishing of the sum of the
(which follows from the vanishing of the sum of the 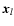 ,
or in a
more geometric way, from the fact that each of these cross products
equals twice the area of the triangle), all angles
,
or in a
more geometric way, from the fact that each of these cross products
equals twice the area of the triangle), all angles 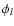 will be
either positive or negative; in particular, they all will be positive
if the closed path from
will be
either positive or negative; in particular, they all will be positive
if the closed path from 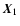 to
to 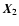 to
to 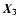 to
to 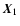 goes around the triangle counter-clockwise. We also observe that
this convention for the angles implies that the sum of the internal
angles of the triangle will be
goes around the triangle counter-clockwise. We also observe that
this convention for the angles implies that the sum of the internal
angles of the triangle will be 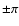 depending on the orientation;
however, this ambiguity will not generally play a role, since all
relations for angles are defined modulo
depending on the orientation;
however, this ambiguity will not generally play a role, since all
relations for angles are defined modulo 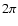 .
In the following we
will call a triangle positively (respectively, negatively) oriented if
the sum of its internal angle is
.
In the following we
will call a triangle positively (respectively, negatively) oriented if
the sum of its internal angle is 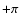 (
(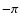 ).
The relation between the
).
The relation between the 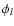 and the
and the 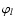 is given by
is given by
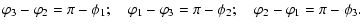 |
|
|
(1) |
Let
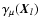 be the Cartesian components of the shear at point
be the Cartesian components of the shear at point 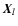 ;
they are defined in terms of the deflection potential
;
they are defined in terms of the deflection potential
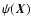 by the differential operation
by the differential operation
![$\gamma_1=[\partial^2\psi/(\partial X_1^2)-\partial^2\psi/(\partial
X_2^2)]/2$](/articles/aa/full/2003/03/aah3784/img49.gif) ,
,
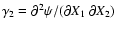 .
We define the Cartesian components of the shear 3PCF as
.
We define the Cartesian components of the shear 3PCF as
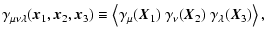 |
|
|
(2) |
where we have made use of the fact that the shear field is assumed to
be a homogeneous random field, so that the 3PCF is invariant under
translations; therefore,
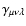 does depend only on
the separation vectors
does depend only on
the separation vectors 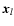 .
Although we also assume that the
random field is isotropic, the Cartesian components
.
Although we also assume that the
random field is isotropic, the Cartesian components
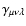 of the 3PCF do not depend just on the
of the 3PCF do not depend just on the
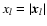 (see below).
(see below).
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip,bb=32 595 267 765]{fig1.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg54.gif) |
Figure 1:
Definitions of the geometry of a triangle. The 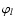 are the orientations of the sides of the triangle relative to the
positive x1-direction, the
are the orientations of the sides of the triangle relative to the
positive x1-direction, the 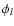 are the interior angles of
the triangle, which are related to the
are the interior angles of
the triangle, which are related to the 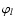 by
(1), provided the orientation of the three points is
as displayed here.
by
(1), provided the orientation of the three points is
as displayed here. |
For any reference direction 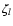 ,
we can define the
tangential and cross components of the shear,
,
we can define the
tangential and cross components of the shear,
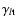 and
and
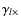 ,
respectively, at point
,
respectively, at point 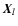 relative to this
direction by
relative to this
direction by
or explicitly in terms of the components,
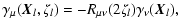 |
|
|
(4) |
where
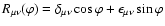 is
the rotation matrix,
is
the rotation matrix,
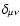 the Kronecker delta, and
the Kronecker delta, and
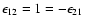 ,
,
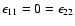 ;
here and in the
following, we identify the tangential component with
;
here and in the
following, we identify the tangential component with 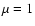 ,
and the
cross component with
,
and the
cross component with 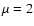 when we write transformation equations
like (4), and we employ the Einstein summation
convention. We notice that, because of the rotation behavior of the
shear, we only need to specify the projection direction
when we write transformation equations
like (4), and we employ the Einstein summation
convention. We notice that, because of the rotation behavior of the
shear, we only need to specify the projection direction 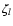 modulo
modulo 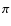 .
.
If the reference directions 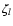 are defined in terms of the
position vectors of the vertices of the triangle, or the side vectors,
and thus rotate in the same way as the triangle as whole, then the
tangential and cross components of the shear are invariant under
rotations and translations of the triangle. For example, the direction
are defined in terms of the
position vectors of the vertices of the triangle, or the side vectors,
and thus rotate in the same way as the triangle as whole, then the
tangential and cross components of the shear are invariant under
rotations and translations of the triangle. For example, the direction
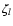 could be chosen as the direction
could be chosen as the direction 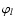 of the opposite
side of the triangle. The 3PCF of these projected shear components
will then depend only on the
of the opposite
side of the triangle. The 3PCF of these projected shear components
will then depend only on the
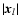 ,
,
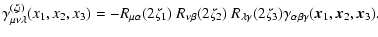 |
|
|
(5) |
The orientation of the triangle becomes important if the arguments of
the 3PCF are written as the three side lengths; in this case, the
triangle is defined only up to a parity transformation. Hence, in
all relations involving only the side lengths of a triangle, we will
assume that the triangle has positive parity. We shall see
in Sect. 4 how the shear 3PCF behaves under parity transformations.
In Eq. (5), the directions 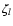 are arbitrary. For a
given set of three points, i.e., for a given triangle, there are
several natural choices for the reference directions; we shall discuss
those in the next subsection. One choice was already mentioned above, namely
the direction
are arbitrary. For a
given set of three points, i.e., for a given triangle, there are
several natural choices for the reference directions; we shall discuss
those in the next subsection. One choice was already mentioned above, namely
the direction 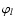 of the side opposite to the corner
of the side opposite to the corner 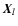 .
We
shall label the corresponding 3PCF with the superscript "s'' (for
``side''),
.
We
shall label the corresponding 3PCF with the superscript "s'' (for
``side''),
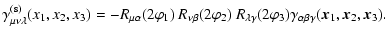 |
|
|
(6) |
In addition to the side projection mentioned above,
there are several other natural choices for the directions along which
the shear can be projected. For each triangle, one can define a number
of "centers''; the direction of the vector connecting the point  with one of these centers can be used to define convenient
components of the 3PCF. The four most important centers are: (1) the
centroid of a triangle; it is the point where the side-bisectors
intersect; (2) the incenter (center of the incircle), which is the
intersection of the three angle-bisectors of the interior angles
with one of these centers can be used to define convenient
components of the 3PCF. The four most important centers are: (1) the
centroid of a triangle; it is the point where the side-bisectors
intersect; (2) the incenter (center of the incircle), which is the
intersection of the three angle-bisectors of the interior angles
 ;
(3) the circumcenter (center of the circumcircle), which is
the point of intersection of the three midperpendiculars, and (4) the
orthocenter, which is the intersection point of the altitudes.
;
(3) the circumcenter (center of the circumcircle), which is
the point of intersection of the three midperpendiculars, and (4) the
orthocenter, which is the intersection point of the altitudes.
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip,bb=45 587 275 757]{fig2.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg75.gif) |
Figure 2:
The orthocenter of a triangle, determined by the
intersection of the three altitudes. The angle between the
altitude of  and the side
and the side 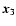 is easily obtained
from the right triangle formed by this altitude and the two sides
is easily obtained
from the right triangle formed by this altitude and the two sides
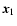 and
and 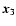 . . |
We now define the tangential and cross components of the shear
relative to the direction of the line connecting the point 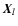 with one of these centers. Since the line connecting
with one of these centers. Since the line connecting 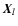 with
the orthocenter (the point "H'' in Fig. 2) is perpendicular
to the side vector
with
the orthocenter (the point "H'' in Fig. 2) is perpendicular
to the side vector 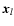 ,
we find for the projection of the shear
relative to the direction of the orthocenter (labeled with superscript
"o'') simply by setting
,
we find for the projection of the shear
relative to the direction of the orthocenter (labeled with superscript
"o'') simply by setting
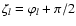 in (4),
in (4),
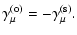 |
|
|
(7) |
Therefore,
we obtain the shear 3PCF for this projection
from Eq. (5)
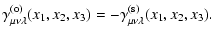 |
|
|
(8) |
Next we consider the center of the incircle. As this is given by the
intersection of the angle-bisectors, we obtain for the direction
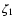 of the line connecting
of the line connecting 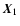 with the incenter (see
Fig. 3)
with the incenter (see
Fig. 3)
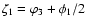 ;
hence,
;
hence,
Using Eqs. (4) and (7), one finds that the
relation between the Cartesian components of the shear and those
defined with respect to the ortho-center is
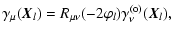 |
|
|
(9) |
so that
Since
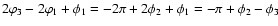 ,
where we used Eq. (1) and the fact that the sum of the
,
where we used Eq. (1) and the fact that the sum of the
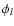 is
is 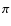 ,
one finally obtains
,
one finally obtains
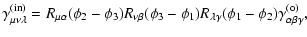 |
|
|
(10) |
where the result for the other two points were obtained from the one
at 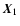 by cyclic permutation of the indices. It should be noted
that in this equation, as in all the following, the angles
by cyclic permutation of the indices. It should be noted
that in this equation, as in all the following, the angles 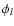 are functions of the sidelengths xl (and the orientation), and not
independent geometrical quantities; hence, an equation like (10) contains only the xl as independent variables.
are functions of the sidelengths xl (and the orientation), and not
independent geometrical quantities; hence, an equation like (10) contains only the xl as independent variables.
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip]{fig3.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg86.gif) |
Figure 3:
The incenter of a triangle is given by the intersection
of the three interior angle-bisectors. |
Next we consider the projection onto the center of the
circumcircle. If 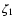 denotes the direction of the line
connecting
denotes the direction of the line
connecting 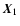 with this center, then the shear components with
respect to this center (denoted by the superscript "out'') read
with this center, then the shear components with
respect to this center (denoted by the superscript "out'') read
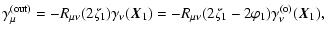 |
|
|
(11) |
where in the second step we used Eq. (9). From Thales'
theorem (see Fig. 5) one finds that
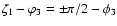 ,
where the sign
,
where the sign 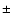 depends on
the orientation of the triangle. Hence,
depends on
the orientation of the triangle. Hence,
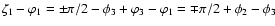 ,
and we see that the sign ambiguity does not play a role
because of the rotation properties of the shear (cf. comment after
Eq. (4)). For the other two points, the corresponding
relations are obtained by cyclic permutations, so that
,
and we see that the sign ambiguity does not play a role
because of the rotation properties of the shear (cf. comment after
Eq. (4)). For the other two points, the corresponding
relations are obtained by cyclic permutations, so that
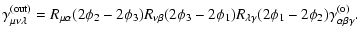 |
|
|
(12) |
Finally, we consider the projection on the center of mass of the
triangle, or the centroid (denoted by the superscript "cen''), which
is the intersection of the three side-bisectors. Denoting by 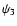 the angle between the side bisector of side x3 and
the angle between the side bisector of side x3 and 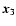 ,
we
obtain from Fig. 4 that
,
we
obtain from Fig. 4 that
where we made use of the sine-theorem, and
is the length of the side-bisector of side x3. From the same figure
we also obtain that
so that
| |
|
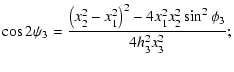 |
|
| |
|
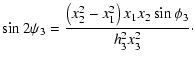 |
(13) |
Analogous relations are obtained for the other two points by cyclic
permutations of the indices. The shear components projected toward the
centroid are then
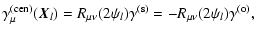 |
|
|
(14) |
where the components of the rotation matrix can be directly obtained
from Eq. (13). For completeness, we give the 3PCF for the
centroid,
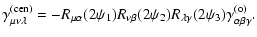 |
|
|
(15) |
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip,bb=45 587 275 757]{fig4.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg100.gif) |
Figure 4:
The centroid of a triangle is the intersection point of
the three side-bisectors. |
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip,bb=30 525 270 756]{fig5.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg101.gif) |
Figure 5:
The circumcenter of a triangle is given by the
intersection of the three midperpendiculars. According to Thales'
theorem, the side x2 subtends the angle 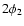 as seen from
the circumcenter; from that, the angle between the lines
connecting the points
as seen from
the circumcenter; from that, the angle between the lines
connecting the points 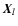 with the circumcenter are easily
obtained by noting that all three of them have equal length.
with the circumcenter are easily
obtained by noting that all three of them have equal length. |


Up: The three-point correlation function
Copyright ESO 2003
![]() ,
,
![]() ,
and define their
difference vectors
,
and define their
difference vectors
![]() ,
,
![]() ,
,
![]() ,
so that
,
so that
![]() (see Fig. 1). Each of the three difference vectors
will be written as
(see Fig. 1). Each of the three difference vectors
will be written as
![]() ,
so that
,
so that
![]() is the orientation of the lth side of the
triangle. Furthermore, we define
is the orientation of the lth side of the
triangle. Furthermore, we define ![]() as being the interior angle
of the triangle at the corner
as being the interior angle
of the triangle at the corner ![]() .
In order to have general
relations, in this paper we will use oriented angles, i.e.
we will attach to each angle a sign indicating its orientation. More
precisely, we will define
.
In order to have general
relations, in this paper we will use oriented angles, i.e.
we will attach to each angle a sign indicating its orientation. More
precisely, we will define
![]() to have the same sign
of the cross product
to have the same sign
of the cross product
![]() (where
(where
![]() ),
and similarly for
),
and similarly for ![]() and
and ![]() .
Note that, since
.
Note that, since
![]() (which follows from the vanishing of the sum of the
(which follows from the vanishing of the sum of the ![]() ,
or in a
more geometric way, from the fact that each of these cross products
equals twice the area of the triangle), all angles
,
or in a
more geometric way, from the fact that each of these cross products
equals twice the area of the triangle), all angles ![]() will be
either positive or negative; in particular, they all will be positive
if the closed path from
will be
either positive or negative; in particular, they all will be positive
if the closed path from ![]() to
to ![]() to
to ![]() to
to ![]() goes around the triangle counter-clockwise. We also observe that
this convention for the angles implies that the sum of the internal
angles of the triangle will be
goes around the triangle counter-clockwise. We also observe that
this convention for the angles implies that the sum of the internal
angles of the triangle will be ![]() depending on the orientation;
however, this ambiguity will not generally play a role, since all
relations for angles are defined modulo
depending on the orientation;
however, this ambiguity will not generally play a role, since all
relations for angles are defined modulo ![]() .
In the following we
will call a triangle positively (respectively, negatively) oriented if
the sum of its internal angle is
.
In the following we
will call a triangle positively (respectively, negatively) oriented if
the sum of its internal angle is ![]() (
(![]() ).
The relation between the
).
The relation between the ![]() and the
and the ![]() is given by
is given by
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip,bb=32 595 267 765]{fig1.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg54.gif)
![]() ,
we can define the
tangential and cross components of the shear,
,
we can define the
tangential and cross components of the shear,
![]() and
and
![]() ,
respectively, at point
,
respectively, at point ![]() relative to this
direction by
relative to this
direction by
![]() are defined in terms of the
position vectors of the vertices of the triangle, or the side vectors,
and thus rotate in the same way as the triangle as whole, then the
tangential and cross components of the shear are invariant under
rotations and translations of the triangle. For example, the direction
are defined in terms of the
position vectors of the vertices of the triangle, or the side vectors,
and thus rotate in the same way as the triangle as whole, then the
tangential and cross components of the shear are invariant under
rotations and translations of the triangle. For example, the direction
![]() could be chosen as the direction
could be chosen as the direction ![]() of the opposite
side of the triangle. The 3PCF of these projected shear components
will then depend only on the
of the opposite
side of the triangle. The 3PCF of these projected shear components
will then depend only on the
![]() ,
,
![]() are arbitrary. For a
given set of three points, i.e., for a given triangle, there are
several natural choices for the reference directions; we shall discuss
those in the next subsection. One choice was already mentioned above, namely
the direction
are arbitrary. For a
given set of three points, i.e., for a given triangle, there are
several natural choices for the reference directions; we shall discuss
those in the next subsection. One choice was already mentioned above, namely
the direction ![]() of the side opposite to the corner
of the side opposite to the corner ![]() .
We
shall label the corresponding 3PCF with the superscript "s'' (for
``side''),
.
We
shall label the corresponding 3PCF with the superscript "s'' (for
``side''),
![]() with one of these centers can be used to define convenient
components of the 3PCF. The four most important centers are: (1) the
centroid of a triangle; it is the point where the side-bisectors
intersect; (2) the incenter (center of the incircle), which is the
intersection of the three angle-bisectors of the interior angles
with one of these centers can be used to define convenient
components of the 3PCF. The four most important centers are: (1) the
centroid of a triangle; it is the point where the side-bisectors
intersect; (2) the incenter (center of the incircle), which is the
intersection of the three angle-bisectors of the interior angles
![]() ;
(3) the circumcenter (center of the circumcircle), which is
the point of intersection of the three midperpendiculars, and (4) the
orthocenter, which is the intersection point of the altitudes.
;
(3) the circumcenter (center of the circumcircle), which is
the point of intersection of the three midperpendiculars, and (4) the
orthocenter, which is the intersection point of the altitudes.
![]() with one of these centers. Since the line connecting
with one of these centers. Since the line connecting ![]() with
the orthocenter (the point "H'' in Fig. 2) is perpendicular
to the side vector
with
the orthocenter (the point "H'' in Fig. 2) is perpendicular
to the side vector ![]() ,
we find for the projection of the shear
relative to the direction of the orthocenter (labeled with superscript
"o'') simply by setting
,
we find for the projection of the shear
relative to the direction of the orthocenter (labeled with superscript
"o'') simply by setting
![]() in (4),
in (4),
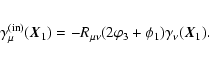
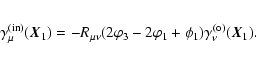
![\begin{figure}
\par\resizebox{88mm}{!}{\includegraphics[clip]{fig3.ps}} \end{figure}](/articles/aa/full/2003/03/aah3784/Timg86.gif)
![]() denotes the direction of the line
connecting
denotes the direction of the line
connecting ![]() with this center, then the shear components with
respect to this center (denoted by the superscript "out'') read
with this center, then the shear components with
respect to this center (denoted by the superscript "out'') read