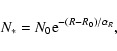 |
(1) |
Following the simple model of Shara et al. (1999), we can estimate the number
of candidates we expect to find in the various regions of our survey.
We assume a thin, exponential disk, where the stellar density follows a
radial exponential law:
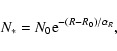 |
(1) |
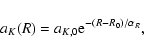 |
(2) |
The WR progenitors, the O stars, should follow this exponential law, but we
must also consider the metallicity dependence for WR formation
(Maeder & Meynet 1994, which modifies
![]() .
.
| WR/O = 0.13 Z/Z0. | (3) |
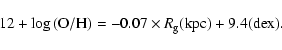 |
(4) |
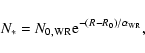 |
(5) |
We now have an expression for WR density and dust extinction, the next ingredient is absolute K magnitudes for WR stars, which are not well-known. From previous spectral analyses, WC absolute K magnitudes range from -3.8 to -5.7 (Smartt et al. 2001; Dessart et al. 2000; Hillier & Miller 1999; Crowther et al. 2002). For late-type WCs, which are predominant at high metallicity, absolute K magnitudes range from -3.8 to -5.0. The absolute K magnitudes of WR134 and WR136, both of WN4-5s type, are -5.47 and -5.64, respectively (Crowther & Smith 1996). The Galactic star WR105 (WN9h) has an absolute magnitude of -6.0 derived from its apparent K magnitude, its distance and extinction at K (Churchwell et al. 1992).
Given that WN and WC stars come from a range of initial masses, they should also have a range in absolute magnitude. Additionally, the luminosity of the WNL phase is greater than that of the WC phase while at comparable temperatures. As expected, it appears from observations that WN and WC stars have a range in absolute magnitude, and the WN star population extends to brighter magnitudes. Let us assume a number distribution according to a Salpeter law, that WN stars are distributed between K -4.0 and -7.0, WC stars between -3.0 and -6.0, and that the WC/WN ratio is 1.2 in the inner galaxy (from the empirical relation for WC/WN and O/H in the Local Group, Massey & Johnson 1998).
With this model, we can make an estimate of the number of candidates we can expect in our data set. In Fig. 11 we show the number of candidates expected per degree of Galactic longitude as a function of longitude, for varying apparent magnitude limits.
Our images cover ![]() 3 degrees of longitude, but
3 degrees of longitude, but ![]() 15% of that is
lost by being on the edges of our strips, and 3 strips are of very low
signal-to-noise due to clouds. This gives us a total of 2.3 degrees
of longitude, covered between
15% of that is
lost by being on the edges of our strips, and 3 strips are of very low
signal-to-noise due to clouds. This gives us a total of 2.3 degrees
of longitude, covered between ![]() 0.5 galactic latitude.
0.5 galactic latitude.
Within that region our model predicts 18 WR stars brighter than K=11,
and 34 brighter than
K=12, or 16 additional stars. Our completeness tests indicate that we
detect ![]() of emission line stars brighter than K=11, and
of emission line stars brighter than K=11, and ![]() brighter than K=12. According to this, we should detect a total of 28
WR stars in this region.
In our second set of data, taken in 2000 at l=316, we cover about one
degree of longitude between
brighter than K=12. According to this, we should detect a total of 28
WR stars in this region.
In our second set of data, taken in 2000 at l=316, we cover about one
degree of longitude between ![]() ,
and expect 4 WR stars.
,
and expect 4 WR stars.
![\begin{figure}
\par\includegraphics[width=7.5cm]{MS3085f11.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg44.gif) |
Figure 11: The number of WR stars expected from our simple model per degree of longitude as a function of Galactic Longitude. |
So far, we have observed all our high priority candidates in the GC region. We have not yet observed any candidates in the Centaurus-Scutum region. In the GC region, we have found four new WR stars. These four stars should be added to those already found in the region through pointed observations. The majority are found in two young clusters, the Arches cluster (Nagata et al. 1995; Cotera et al. 1996), and the Quintuplet cluster (Figer et al. 1999a), though some stars have been found outside clusters as in the present case (Cotera et al. 1999). A full discussion of our detection efficieny and description of the newly discovered WR stars will be given in our upcoming paper on spectroscopic follow-up observations.
Preliminary spectroscopic results are given by Homeier et al. (2002).
Copyright ESO 2003