

Up: A near-infrared survey for
Subsections
Table 2:
Prominent lines in Wolf-Rayet K-band spectra.
Central 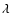 (
(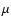 m) m) |
Transition |
Type |
| 2.0587 |
He I 2s-2p |
WN, WC |
| 2.0705/2.0796/2.0842 |
C IV 3p-3d |
WC |
| 2.1126/2.1137 |
He I 4s-3p |
WN, WC |
| 2.1038/2.1152/2.1155/2.1156 |
C III/N III 8-7 |
WC |
| 2.1632 |
He I 7-4 |
WN, WC |
| 2.1652 |
He II 14-8 |
WN, WC |
| 2.166 |
Br 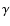 ,
H I 7-4 ,
H I 7-4 |
WN |
| 2.189 |
He II 10-7 |
WN, WC |
| 2.2779 |
C IV 15-12 |
WC |
| 2.3178 |
C IV 17-13 |
WC |
| 2.3470 |
He II 13-8 |
WN |
Data is reproduced from Table 2 of Figer et al. (1997), see references therein. Wavelengths listed are vacuum wavelengths.
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{aa3085f1a.eps}\hspace{5mm}
\includegraphics[width=8.5cm]{aa3085f1b.eps} }
\end{figure}](/articles/aa/full/2003/02/aa3085/Timg15.gif) |
Figure 1:
A representative sample of WR stars with filter transmission
curves overplotted, WN stars left panel and WC stars right
panel. Dotted curves represent the line filters at 2.06, 2.08, 2.166,
and 2.19 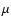 m. Dot-dashed lines represent the continuum filters at
2.03, 2.14, and 2.248 m. Dot-dashed lines represent the continuum filters at
2.03, 2.14, and 2.248 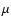 m. The He II filter transmission curve is
difficult to see in the left panel due to the strong He II lines in the
WN stars. WR spectra in both panels are kindly provided by P. Eenens. m. The He II filter transmission curve is
difficult to see in the left panel due to the strong He II lines in the
WN stars. WR spectra in both panels are kindly provided by P. Eenens. |
In Table 1 we present central wavelengths and FWHMs for
our chosen set of K-band filters (Blum & Damineli 1999a; Homeier et al. 2002).
Four filters are centered on
the characteristic stellar wind emission lines of He I 2.06 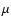 m,
C IV 2.08
m,
C IV 2.08 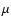 m, H I Br
m, H I Br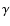 2.166
2.166 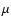 m,
and He II 2.189
m,
and He II 2.189 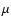 m, and the additional three continuum filters
are at 2.03
m, and the additional three continuum filters
are at 2.03 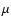 m, 2.14
m, 2.14 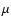 m, and 2.248
m, and 2.248 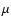 m. Thus each line filter
measurement has a continuum point to the red and blue.
It is extremely important to have continuum points to the
red and the blue of each line filter because of the variation in continuum
slope caused by dust extinction.
m. Thus each line filter
measurement has a continuum point to the red and blue.
It is extremely important to have continuum points to the
red and the blue of each line filter because of the variation in continuum
slope caused by dust extinction.
In Table 2 we list the most prominent emission lines in WR
spectra, and the filter response curves are overplotted in
Figs. 1a and 1b for unpublished K-band spectra of WN and WC stars kindly
provided by P. Eenens.
In both, the three continuum filters are overplotted as
dot-dash lines, and the four line filters as dotted lines. This illustrates
the sensitivity of the 2.17 and 2.19 filters to WN stars, whereas
the 2.06 and 2.08 filters are most sensitive to WC stars.
![\begin{figure}
\par\includegraphics[width=15.85cm]{MS3085f2.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg16.gif) |
Figure 2:
Map of the observations from 1996, 1997, and 1998. The x and y axes are in
Galactic coordinates. Lines of constant right ascension are overplotted in
intervals of 2 min as dotted lines, and lines of constant
declination are overplotted every half degree as solid lines. |
![\begin{figure}
\par\includegraphics[width=11.75cm]{MS3085f3.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg17.gif) |
Figure 3:
The same data as in Fig. 2 overplotted on the 90 cm
radio image of the Galactic Center region presented in LaRosa et al. 2000.
Major features are labeled, and the small rectangle indicates the approximate
position of Fig. 5. |
![\begin{figure}
\par\includegraphics[width=15cm]{MS3085f4.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg18.gif) |
Figure 4:
Same as Fig. 2, but for the 2000 data. |
![\begin{figure}
\par\includegraphics[width=11cm]{aa3085f5.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg19.gif) |
Figure 5:
This is a sample of our data from 1996. The image shown here was
taken with the 2.248 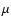 m filter. The center coordinates
are 17:46:35.7, -28:42:35 J2000. The y dimension spans m filter. The center coordinates
are 17:46:35.7, -28:42:35 J2000. The y dimension spans
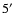 and the
x dimension spans
and the
x dimension spans 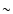 19 19
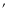 .
South is up and east is to the
left. Large scale variations in stellar density are apparent and caused by
intervening dark clouds. .
South is up and east is to the
left. Large scale variations in stellar density are apparent and caused by
intervening dark clouds. |
In 1996 the survey was begun at the 1.5m at the Cerro Tololo Interamerican
Observatory, and continued in 1997, 1998, and 2000. For 1996, 97, and
98 we used the same telescope and instrument configuration: the Cerro
Tololo Infrared Imager (CIRIM) with the f/8 mode, giving us a
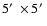 field of view and
field of view and
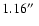 per
pixel. In 2000, we used the Ohio State Infrared Imaging Spectrometer
in the f/8 mode for a
per
pixel. In 2000, we used the Ohio State Infrared Imaging Spectrometer
in the f/8 mode for a
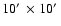 field of view and
field of view and
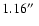 per pixel. Our images are taken in "strips'' composed
of 35-45 images. We offset 1/3 of a chip in RA (1996-1998 data)
or Dec (2000 data), keeping the other coordinate constant. Thus each
spot on the image strip is a composite of three exposures. Images have
been obtained over
per pixel. Our images are taken in "strips'' composed
of 35-45 images. We offset 1/3 of a chip in RA (1996-1998 data)
or Dec (2000 data), keeping the other coordinate constant. Thus each
spot on the image strip is a composite of three exposures. Images have
been obtained over  3 degrees of longitude between
3 degrees of longitude between  0.5
near the Galactic Center. This is shown in Fig. 2, and
overplotted on a 90 cm image of the Galactic Center region in Fig. 3. In 2000, we moved outward along the plane to l = 316, at the edge of Centaurus looking towards the Scutum-Crux spiral arm. In
this region we obtained
0.5
near the Galactic Center. This is shown in Fig. 2, and
overplotted on a 90 cm image of the Galactic Center region in Fig. 3. In 2000, we moved outward along the plane to l = 316, at the edge of Centaurus looking towards the Scutum-Crux spiral arm. In
this region we obtained  1 degree of Galactic longitude between
1 degree of Galactic longitude between 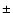 1.0 Galactic Latitude. This is shown in Fig. 4. A sample
of our data is shown in Fig. 5, with a small rectangle
indicating the approximate position on the 90 cm radio image in Fig. 3.
1.0 Galactic Latitude. This is shown in Fig. 4. A sample
of our data is shown in Fig. 5, with a small rectangle
indicating the approximate position on the 90 cm radio image in Fig. 3.
Data reduction is performed with the CIRRED package of routines in
IRAF![[*]](/icons/foot_motif.gif) ,
written specifically for CIRIM and OSIRIS
,
written specifically for CIRIM and OSIRIS![[*]](/icons/foot_motif.gif) reductions by
R. D. Blum. The
reduction steps are as follows. First, we trim the flat-field images if
needed. For each filter there is a set of images taken with the lamps
on and off. We take the median of each set of "on'' and "off'' frames to make
a single "on'' and "off'' image. We subtract
the "off'' frame from the "on'' frame to make a flat image, which is then
normalized by the mean. A bad pixel mask is made by comparing the dome
flats with the lights on and the lights off and using the histogram of
pixel intensities to distinguish good and bad
pixels. This bad pixel mask is then used to correct the flat field
images.
reductions by
R. D. Blum. The
reduction steps are as follows. First, we trim the flat-field images if
needed. For each filter there is a set of images taken with the lamps
on and off. We take the median of each set of "on'' and "off'' frames to make
a single "on'' and "off'' image. We subtract
the "off'' frame from the "on'' frame to make a flat image, which is then
normalized by the mean. A bad pixel mask is made by comparing the dome
flats with the lights on and the lights off and using the histogram of
pixel intensities to distinguish good and bad
pixels. This bad pixel mask is then used to correct the flat field
images.
Next, the survey images are trimmed if needed, linearity corrected
with IRLINCOR, divided by exposure time, fixed with the bad pixel
mask, and divided by the flat field image. Then the entire stack of
images within a strip is used to make a sky image for each filter. The
images are median combined using "minmax'' rejection with approximately half
the images thrown out to reject contributions
from stars. The resulting sky image is subtracted from each of the
individual frames, and a constant is added back to maintain an
appropriate sky level in the reduced image. These images are then
assembled into a strip approximately one degree long by
cross-correlation of the overlapping regions on each frame. Finally,
we derive astrometric solutions for each of our strips by comparing
the 248 filter images to the 2MASS catalog images from IPAC and the
IRAF task CCMAP.
Each frame is analyzed with DoPhot (Schechter et al. 1993). DoPhot
identifies, classifies, and performs photometry on objects in an
image. It makes successive passes over the image, subtracting the
objects and searching in the next pass for fainter objects. The model
parameters are found iteratively in the image itself, with reasonable first
guesses supplied by the user in parameter files.
Our program has no strict requirement for calibrated photometry since
emission-line stars are found through continuum independent line
indices. Furthermore, much of the data was taken in non-photometric
conditions. However, it is of interest to have an
order-of-magnitude calibration in order to help assess how deep the
images typically go. We have done a comparison between a typical
image section of one of our image strips and the 2MASS survey images.
We compared our instrumental magnitude for the 2.06 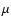 m filter,
which is the least sensitive of all our filters due to the combination of
transmission efficiency and filter width. 2MASS magnitudes were
obtained from the Infrared Science Archive (IRSA) through the GATOR
query page. Our comparison shows that an instrumental magnitude of
-3 corresponds roughly to an apparent K magnitude of 12 for this
strip.
m filter,
which is the least sensitive of all our filters due to the combination of
transmission efficiency and filter width. 2MASS magnitudes were
obtained from the Infrared Science Archive (IRSA) through the GATOR
query page. Our comparison shows that an instrumental magnitude of
-3 corresponds roughly to an apparent K magnitude of 12 for this
strip.
![\begin{figure}
\par\includegraphics[width=11.5cm]{aa3085f6.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg24.gif) |
Figure 6:
The
fraction of stars recovered in artificial star experiments for the
four line images and its dependence on the continuum magnitude of the
star. See text. |
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg25.gif) |
Figure 7:
Standard deviation of the difference between the input color index and the
measured line index for the 2.06 line artificial star experiment. The
continuum magnitude is shown on the top of each small panel. The error
in line index does not depend on line strength, but does depend on
continuum magnitude. |
To test our sensitivity to emission line stars, we created grids of
fake stars with continuum magnitudes ranging from -2.0 to -7.0 in
instrumental continuum magnitude, and
emission line magnitudes ranging from 0.1 to 1.0 magnitudes
brighter than the continuum. That is, we created grids where 100 stars have
continuum (2.03, 2.14, and 2.248 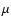 m) magnitudes of -2.0, and
line (2.062, 2.077, 2.166, 2.191
m) magnitudes of -2.0, and
line (2.062, 2.077, 2.166, 2.191 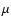 m) magnitudes of -2.1, 100 with the
same continuum magnitudes, and line magnitudes of -2.2, and so on.
At each step in continuum magnitude, we added 1000 stars with varying
line magnitude.
m) magnitudes of -2.1, 100 with the
same continuum magnitudes, and line magnitudes of -2.2, and so on.
At each step in continuum magnitude, we added 1000 stars with varying
line magnitude.
The psf for each filter image was constructed
using several bright and relatively well-isolated stars in the image
and the IRAF tasks
"pstselect'' and "psf''. Images were then created using
"mkobjects''. These images were analyzed in exactly the same way as a real
image. In Fig. 6 we plot
the fraction recovered at increasing brightness of the continuum magnitude.
There is a dependence on overall brightness, but no significant dependence
on emission line strength. This is similar to what one would expect
for a broad-band color.
The survey is limited by crowding (especially in the GC region) and
the relatively coarse angular resolution element provided by the 1.5 m
telescope. Given the order-of-magnitude comparison made above with
the comparison to 2MASS, th 2.06 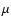 m filter the data are
m filter the data are
 75% complete at K = 12 mag. However, the photometric accuracy
decreases at faint magnitudes. This is shown in Fig. 7 for
the same stars that are plotted in Fig. 6. The line shown
here is the
75% complete at K = 12 mag. However, the photometric accuracy
decreases at faint magnitudes. This is shown in Fig. 7 for
the same stars that are plotted in Fig. 6. The line shown
here is the
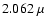 m line, but all lines (2.077, 2.166, and 2.191
m line, but all lines (2.077, 2.166, and 2.191 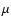 m) show very similar behavior.
m) show very similar behavior.
In this section we detail our candidate selection procedure. As a first step,
the object coordinates must be transformed to a single system. We
have arbitrarily chosen to use the longest wavelength filter image as
our template.
Thus, we scale and offset the coordinates for objects in the other lists
to the 2.248 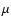 m object list. This is accomplished with the "transform''
package which accompanies DoPhot. Transform uses a triangular search routine
to match stars in different images by comparing the relative scales and
orientations of stars in groups of three. Hereafter, we refer to the task
as "offset''.
m object list. This is accomplished with the "transform''
package which accompanies DoPhot. Transform uses a triangular search routine
to match stars in different images by comparing the relative scales and
orientations of stars in groups of three. Hereafter, we refer to the task
as "offset''.
We look at each emission-line filter separately, meaning we consider sets
of three filters each time, the line and its two continuum filters
(2.03 and 2.14 for 2.06 and 2.08; 2.14 and 2.248 for 2.17 and 2.19).
The raw output of DoPhot contains 10 000 to 30 000 objects per image,
and this output must first be gleaned for stars with good statistics.
The first cut is on object type. In the DoPhot output each object is
assigned a number indicating the whether it is a star or a galaxy, and
how well it thinks it can determine the magnitude. There are three object
types we are interested in: 1 s are single stars with good statistics, 7 s
are single stars with decent statistics, and 3 s are fit as
members of a blend of 2
single stars. During the transformation to 2.248 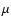 m coordinates,
"offset'' keeps track of the object types in both lists, and records it
in the output file. We keep only combinations
of single stars (such as 11 s, 17 s, 71 s, or 77 s) and doubles (33 s). We
throw out stars which have been classified as a member of a double in
one image and a single star in another, as the photometry in this case
is very unreliable.
m coordinates,
"offset'' keeps track of the object types in both lists, and records it
in the output file. We keep only combinations
of single stars (such as 11 s, 17 s, 71 s, or 77 s) and doubles (33 s). We
throw out stars which have been classified as a member of a double in
one image and a single star in another, as the photometry in this case
is very unreliable.
After cleaning the lists for object type, we perform a cut on photometric
error. The error is calculated simply as the errors of the individual
magnitudes added in quadrature.
The error cut is a free parameter in our selection routine, but we usually
select it to be between 0.1 and 0.3 mag.
We now have three lists of objects, cleaned on the basis of object type and
error. The coordinates in these three lists are now matched, and a
"line index'' is computed as the magnitude
difference between the measured value and the expected value derived
from a linear interpolation using the two continuum filters magnitudes.
Essentially all stars in the images should have a constant line index
(which is not zero due to filter transmission differences and sky
transmission variations), that we can subtract to set the mean line
index to zero. When the nights were not photometric,
systematic line index variations as a function of position
(time) along the strip occur. These are relatively straightforward to
account for since they produce large scale changes in the line indices with
position on the image. In our analysis we subtract these variations
by calculating a "mean neighbor index'' for each star, using a bin
centered on the star, with a size between 50-100 pixels.
Smaller bins produce output with less scatter, but the bin must be large
enough to contain stars to compute a significant "neighbor index''.
This mean value is then subtracted from the individual objects.
![\begin{figure}
\par\includegraphics[width=8.5cm]{MS3085f8.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg28.gif) |
Figure 8:
The scatter as a function of 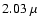 m magnitude is fit
with a linear function to aid in candidate selection. m magnitude is fit
with a linear function to aid in candidate selection. |
We also consider the scatter in line index
as a function of the short wavelength continuum magnitude. An example
is shown in Fig. 8, where the standard deviation in
line index is fit as a linear function of short wavelength continuum
magnitude. Our final selection is done by
considering the line index, the error on this index, and the scatter in
line index at this magnitude. We employ a criterion similar to the "S''
parameter employed by Damineli et al. (1997).
An example of our photometry and candidate selection is shown in
Figs. 9 and 10, and
candidate emission line objects are overplotted as asterisks. One is a
confirmed WR star of late WC subtype (line index  ,
inst. mag.
,
inst. mag. 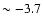 )
(Homeier et al. 2002). In right hand panel of each
figure is the the same data plotted, but without correcting for
systematic positional variations in line index as described above. One
can see that the apparent scatter is larger for the objects in the
right-hand panels, and in the case of the 2.08 filter, it affects which
objects are chosen as emission-line candidates. In this particular
case, a bona-fide WR star would be missed.
)
(Homeier et al. 2002). In right hand panel of each
figure is the the same data plotted, but without correcting for
systematic positional variations in line index as described above. One
can see that the apparent scatter is larger for the objects in the
right-hand panels, and in the case of the 2.08 filter, it affects which
objects are chosen as emission-line candidates. In this particular
case, a bona-fide WR star would be missed.
![\begin{figure}
\par\includegraphics[width=5.8cm]{MS3085f9a.eps}\hspace*{1cm}
\includegraphics[width=5.8cm]{MS3085f9b.eps}\end{figure}](/articles/aa/full/2003/02/aa3085/Timg29.gif) |
Figure 9:
2.06 Filter: an example of our photometric data and candidate
selection. The
stars marked with asterisks are emission line candidates, and one is a
confirmed WR star (cindex  ,
mag ,
mag 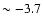 ;
Homeier et al. 2002).
In the right panel is the same but without correcting for positional
line index variations; see text. ;
Homeier et al. 2002).
In the right panel is the same but without correcting for positional
line index variations; see text. |
![\begin{figure}
\par\includegraphics[width=5.8cm]{MS3085f10a.eps}\hspace*{1cm}
\includegraphics[width=5.8cm]{MS3085f10b.eps}\end{figure}](/articles/aa/full/2003/02/aa3085/Timg31.gif) |
Figure 10:
Same as Fig. 9, but for the 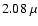 m filter.
The confirmed WR star is located at index m filter.
The confirmed WR star is located at index  ,
mag ,
mag 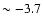 . . |
We also use image subtraction as a way to select high priority candidates.
This step is only performed for those objects that are
selected as photometric candidates.
All procedures discussed here are accomplished with standard IRAF routines.
An image section is selected within +/-125 pixels of a photometric
candidate's x position, and a y pixel range from 1 to 250 pixels. First
the images are cross-correlated and shifted to a common position.
The two continuum filters
are averaged and this result is normalized by the mean. The line
filter is also normalized by the mean and then divided by the averaged,
normalized continuum image. The result is displayed on the screen and
examined visually. We have found that this provides a useful and necessary
check on the photometric selection. Effects such as bad pixels and
residual images are easily seen with this method.
We will discuss candidate selection in further detail in the upcoming paper
on the spectroscopic follow-up (Homeier et al. 2003, in prep).


Up: A near-infrared survey for
Copyright ESO 2003
![\begin{figure}
\par\mbox{\includegraphics[width=8.5cm]{aa3085f1a.eps}\hspace{5mm}
\includegraphics[width=8.5cm]{aa3085f1b.eps} }
\end{figure}](/articles/aa/full/2003/02/aa3085/Timg15.gif)
![\begin{figure}
\par\includegraphics[width=15.85cm]{MS3085f2.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=11.75cm]{MS3085f3.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=15cm]{MS3085f4.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=11.5cm]{aa3085f6.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{fig7.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg25.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm]{MS3085f8.eps} \end{figure}](/articles/aa/full/2003/02/aa3085/Timg28.gif)