4 The numerical model

4.1 Parameters of binary

For a numerical investigation, we have chosen a binary with parameters that are typical for binary Be stars. Since Be stars are most abundant around the spectral class B2, we have chosen parameters corresponding to a normal main-sequence B2 star according to the empirical calibration by Harmanec (1988) and adopted a mass ratio of 0.1 which is also typical for known Be binaries. In particular, we used the mass of Be star (star 1) $M_1=8.6M_\odot$, mass of star 2 $M_2=0.86M_\odot$, binary mass ratio q=M₂/M₁=0.1, binary separation $A=121R_\odot$, and orbital period $P=50^{\mbox{d}}$. Inner Lagrangian point is then located at the distance of $x_{L_1}=87R_\odot$ from the centre of star 1. The equatorial radius of the Be star $R_1=4.6R_\odot$ was chosen. In accordance with the above considerations we assumed the Be component to be large enough to reach the `asynchronous' Roche lobe, i.e. that $x_{L_1^{\rm rot}}=R_1$. Using the adopted values of $x_{L_1^{\rm rot}}/A$ and q, one gets the asynchronicity parameter of Be star $f=\Omega _\star /\Omega$ via Eq. (4). In this case, f is equal to 128.6 (implying that the period of rotation of the Be star is 0 $^{\rm d}\!\!.$39). The value of linear velocity at $L_1^{\rm rot}$ point in the adopted coordinate system is equal to $V_{\rm rot}=(\Omega_\star-\Omega)\cdot x_{L_1^{\rm rot}}=594$ km s^-1. Note that the value of the critical velocity of a single star with the same mass and radius is equal to $V_{\rm br}=\sqrt{GM_1/R_1}=599$ km s^-1. This means that the value of velocity in $L_1^{\rm rot}$ point equals 99.2% of the critical velocity.

As pointed out above, the matter located in $L_1^{\rm rot}$ can reach the L₁ point only when it gets some extra energy $\Delta E$. Figure 4 shows that for the adopted values of q and f it would be necessary to add energy $\Delta E=10.5\cdot A^2\Omega^2$ to reach L₁. For the binary in question, the thermal energy needed to provide such an energy excess would require temperatures of at least 1.86 millions of K. In the numerical model, we actually adopt the value of effective temperature corresponding to a normal star of a similar mass, 22 900 K. One then gets $\Delta E=0.013\cdot A^2\Omega^2$, and the matter outflowing from the $L_1^{\rm rot}$ point cannot get to distances larger than $R=9.1R_\odot\approx2R_1$. Hence, one has to expect formation of an envelope extending to a few stellar radii.

4.2 Gas-dynamical equations

To describe the gas flow, we have used 3-D gas-dynamical equations in cylindrical coordinates. We have modified the original conservative form of equations in cylindrical coordinates to obtain a system similar to the system of gas-dynamical equations in Cartesian coordinates. This approach permits us to treat the flow near the axis more accurately (see, e.g., Pogorelov et al. 2000). The corresponding equations are:

$$\partial_t\rho +\partial_r\rho v_r +\frac{1}{r}\partial_\varphi\rho v_\varphi +\partial_z\rho v_z= -\frac{\rho v_r}{r},$$

$$\begin{array}{l} \partial_t\rho v_r +\partial_r\left(\vphanto... ...\frac{v_\varphi^2-v_r^2}{r} +2\rho\Omega v_\varphi, \end{array}$$

$$\begin{array}{l} \partial_t\rho v_\varphi +\partial_r\rho v_r... ...Phi -\rho\frac{2v_r v_\varphi}{r} -2\rho\Omega v_r, \end{array}$$

$$\begin{array}{l} \partial_t\rho v_z +\partial_r\rho v_r v_z +... ...\right)=-\rho\partial_z\Phi -\rho\frac{v_r v_z}{r}, \end{array}$$

$$\begin{array}{l} \partial_t\rho E +\partial_r\rho v_r h +\fra... ...i -\rho v_z\partial_z\Phi -\rho\frac{v_r h}{r}\cdot \end{array}$$

Here $\partial_t\equiv\partial/\partial t$, $\partial_r\equiv\partial/\partial r$, $\partial_\varphi\equiv\partial/\partial\varphi$, $\partial_z\equiv\partial/\partial z$, $\rho$ is the density, ${\vec v}=(v_r, v_\varphi, v_z)$ the velocity vector, P pressure, $E=\varepsilon+\hbox{$~^{1}\!/_{2}$ }\vert{\vec v}\vert^2$ the full specific energy, $\varepsilon$ specific internal energy, and $h=\varepsilon+P/\rho+\hbox{$~^{1}\!/_{2}$ }\vert{\vec v}\vert^2$ specific full enthalpy. Gas-dynamical equations are written in the adopted co-rotating frame (i.e. in the frame where the centres of stars are in rest), so the Coriolis force is included in momentum equations. As usual, the system of gas-dynamical equations is closed using the equation of state. The equation of state of a perfect gas $P=(\gamma-1)\rho\varepsilon$ was adopted, $\gamma$ being the adiabatic index. In calculations, we adopted the value of $\gamma$ very close to 1 to mimic the energy losses due to radiative cooling (see, e.g., Sawada et al. 1986; Bisikalo et al. 1998). The Roche potential in cylindrical coordinates has the following form:

$$\begin{array}{l} \Phi=-\frac{GM_1}{\sqrt{r^2+z^2}} -\frac{GM_... ...t(\frac{M_2}{M_1+M_2}\right)^2Ar\cos\varphi\right). \end{array}$$

4.3 The finite-difference model

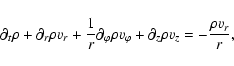
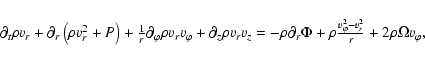
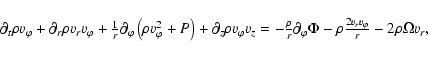
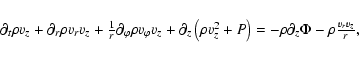
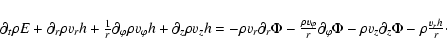
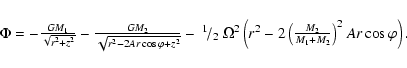
To solve the system of gas-dynamical equations we used a monotonic Roe's scheme (Roe 1986) of first-order approximation with Osher's flux limiters (Chakravarthy & Osher 1985) that increases the order of approximation and leaves the scheme monotonous.

Gas flow was simulated in a cylinder $r\le1.1\cdot x_{L_1}=95R_\odot$, $0\le z\le 50R_\odot$ (because of symmetry with respect to the equatorial plane, calculations could only be conducted in the upper half-space). Non-uniform finite-difference grids (denser near the Be star and the equatorial plane) containing $50\times25\times30$ gridpoints on r, z, and $\varphi$, respectively, were used.

As for the initial condition, we adopted a rarefied gas with $\rho_0=10^{-6}$, P₀=10^-4, and ${\bf v_0}=0$.

The boundary conditions were defined as follows: in the gridpoints that correspond to $L_1^{\rm rot}$ we adopted the condition of injection of matter: $\rho(L_1^{\rm rot})=1$, $T(L_1^{\rm rot})=22~900~\mbox{K}$, which corresponds to the sound velocity $c(L_1^{\rm rot})=14~\mbox{km}~\mbox{s}^{-1}$, $v_r(L_1^{\rm rot})=c(L_1^{\rm rot})$, $v_\varphi(L_1^{\rm rot})=594~\mbox{km}~\mbox{s}^{-1}$, $v_z(L_1^{\rm rot})=c(L_1^{\rm rot})$. Note that an arbitrary value of the boundary density $\rho_0$ can be chosen since the system of equations can be scaled with respect to $\rho$ and P. To derive the true values of density in a specific system with a known mass loss rate, the calculated densities must simply be changed in accordance with the scale determined from the ratio of the true and model mass-loss rate. The boundary conditions were derived by solving the Riemann problem between the gas parameters ( $\rho_0,~{\vec v}_0,~P_0$) in $L_1^{\rm rot}$ point and the parameters in the computation gridpoint closest to it (see, e.g., Sawada et al. 1986; Sawada & Matsuda 1992, or Bisikalo et al. 1998). A full absorption of matter was assumed for the rest of the Be-star surface and for the outer boundary of the computational domain. We have verified that the outer boundary has virtually no effect on the results of computations. The boundary condition at the stellar surface is more important and less clear. However - considering the strong gravitational pull of the massive Be star and centrifugal acceleration, insufficient to cause a mass outflow - we believe that the assumption of the full absorption of matter is legitimate and a physically correct one.

The 3-D gas-dynamical calculations represent a very time-consuming task even for the most powerful present-day computers. That is why for this first investigation we followed the mass outflow only for the minimum interval of time needed. The calculations started as an injection into vacuum and converged to a more or less stable solution after about one third of the orbital period. They were continued to about one full orbital cycle after the emerging pattern of variations remained stable within the adopted accuracy. It is conceivable that future modelling, which we plan to continue until truly steady-state situation, will reveal a somewhat different structure of the envelope. However, it cannot alter our principal finding that the duplicity of a B star can lead to the formation of Be envelope even in a detached binary system.