3 Physical model

Let us consider a single, rapidly rotating star. When the velocity of rotation on equator $V_{\rm rot}$ will reach the Keplerian (also called break-up) velocity $V_{\rm br}=\sqrt{GM/R}$, the centrifugal and gravitational attractive forces will compensate each other:

$$F_{\rm cfg}\equiv\frac{V_{\rm rot}^2}{R}=\frac{GM}{R^2}\equiv F_{\rm grav}.$$

In such situations, the presence of a pressure gradient (not counterbalanced by other forces) permits the matter to outflow from the equatorial belt (called the Roche limit). A particle with specific kinetic energy $\simeq$ $V_{\rm br}^2/2$ rotates along closed trajectories and forms an envelope. To escape to infinity the particle would need to aquire additional energy and reach the parabolic velocity $V=\sqrt{2}V_{\rm br}$.

Figure 1: Relative change in the position of the inner Lagrangian point for the systems with non-synchronous rotation of components $x_{L_1^{\rm rot}}/x_{L_1}$ as a function of the degree of non-synchronous rotation $f=\Omega _\star /\Omega$ for two values of the mass ratio: q=0.1 and q=1. The inserted panel shows the dependence $x_{L_1^{\rm rot}}/x_{L_1}$ vs. q for large values of f.

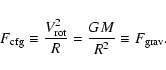
The situation changes dramatically if the same star is a component of a binary system. Let us consider a binary with a spin-orbit synchronization (the velocities of angular rotation of both components are equal to the velocity of angular revolution of the system) and let us use a Cartesian coordinate system that rotates with an angular velocity $\Omega$ and has its origin in the centre of star 1. The X axis is directed toward star 2, Z axis is parallel to the vector of orbital revolution, and Y axis is so oriented to define a right-hand coordinate system. There are several forces acting on a test particle located between the binary components: gravitational attraction of the two binary components, the pressure gradient, and two forces related to the co-rotating frame used: the centrifugal and Coriolis force. The law of motion of such a test particle was first investigated by Roche (1848,1851) in a ballistic approach (i.e. ignoring the pressure force) as a solution of a restricted three-body problem (assuming the mass to be concentrated into two point masses); for a different formulation, see also Hill (1905). The force field (without Coriolis force and the pressure gradient) in cases of a spin-orbit synchronism can be described by the standard Roche potential $\Phi$:

$$\begin{array}{l} \Phi=-{\displaystyle\vphantom{x^2_2}GM_1\ove... ...style\vphantom{x^2_2}M_1+M_2}\right)^2+y^2\right)~, \end{array}$$ (1)

where M₁, M₂ are the two point masses, A is binary separation, $\Omega$ is the angular velocity of orbital motion, and x, y, z are Cartesian coordinates in the adopted frame.

Figure 2: Roche equipotentials (dashed lines) and equipotentials of "asynchronous'' potential $\Psi$ (solid lines) for q=0.1 and different values of f. An arrow shows the linear velocity in $L_1^{\rm rot}$ point which amounts to $0.58~A\Omega$ for the upper panel, $1.88~A\Omega$ for the middle one, and $4.45~A\Omega$ for the bottom panel (the scale of the absolute value of velocity is different for each panel).

The presence of additional forces (absent in the case of a single star) results in violation of equilibrium in the inner Lagrangian point L₁. In particular, the pressure gradient cannot be counterbalanced there by the gradient of the Roche potential. Hence, as soon as the star expands and fills the cricital Roche lobe, matter begins to flow towards the binary companion in the vicinity of L₁ point but not from the entire equatorial zone. The position of inner Lagrangian point L₁ can be derived from equation $\nabla\Phi=0$, which can be rewritten after Kopal (1959):

$$\left(\frac{x_{L_1}}{A}\right)^{-2}-\frac{x_{L_1}}{A} =q\left... ...L_1}}{A}\right)^{-2} -\left(1-\frac{x_{L_1}}{A}\right)\right),$$ (2)

where q=M₂/M₁ denotes the mass ratio.

In case of asynchronous rotation of star 1, we should also include centropedal acceleration and Coriolis force into the equilibrium conditions. The presence of these two terms is related to the motion of the stellar matter in the adopted co-rotating frame. In such a case, the force field at the stellar surface is given by asynchronous Roche potential (see, e.g., Plavec 1958; Kruszewski 1963; or Limber 1963):

$$\Psi=\Phi-\hbox{$~^{1}\!/_{2}$ }(\Omega_\star^2-\Omega^2) (x^2+y^2)$$ (3)

where $\Omega_\star$ is the angular velocity of rotation of the star in question. Similar to the synchronous case it is possible to introduce a concept of the inner Lagrangian point for asynchronous rotation, $L_1^{\rm rot}$, i.e. a point where the pressure gradient ceases to be counterbalanced by other forces and where the matter begins to flow towards the companion when reaching this point. The position of this point is given by the condition $\nabla\Psi=0$ which leads to the following equation (see, e.g., Pratt & Strittmatter 1976)

$$\left(\frac{x_{L_1^{\rm rot}}}{A}\right)^{-2}-f^2\frac{x_{L_1... ...t)^{-2} -\left(1-f^2\frac{x_{L_1^{\rm rot}}}{A}\right)\right),$$ (4)

which is similar to Eq. (2) valid for synchronous rotation. In this equation $f=\Omega _\star /\Omega$ and the sign of f does not affect the solution, i.e., the sense of the stellar rotation in the laboratory coordinate system does not affect the position of $L_1^{\rm rot}$. Therefore - without loss of generality - we consider only the cases of $f\ge0$, i.e. cases when the directions of stellar rotation and binary revolution are the same. The ratio $x_{L_1^{\rm rot}}/x_{L_1}$ as a function of q and f is shown in Fig. 1. It is obvious that for stellar rotation rates slower than the orbital revolution (f<1), the "non-synchronous'' Roche lobe is larger than the standard Roche lobe, achieving maximum for f=0. When the star rotates faster than the binary revolves, the "non-synchronous'' Roche lobe becomes smaller than the standard one. Note that formally $x_{L_1^{\rm rot}}/x_{L_1}\to0$ as $f\to\infty$. In real binaries, however, the position of $x_{L_1^{\rm rot}}$ is actually limited by the break-up rotation velocity of the star in question, so that $x_{L_1^{\rm rot}}/A$ cannot be smaller than $(\Omega_{\rm br}/\Omega)^{-2/3}(q+1)^{-1/3}$.

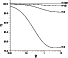Figure 3: The ratio of linear velocity in $L_1^{\rm rot}$ point (in observer's coordinate system) to critical velocity $\eta=\Omega_\star\cdot x_{L_1^{\rm rot}}/\protect\sqrt{GM_1/x_{L_1^{\rm rot}}}\cdot100\%$ vs. q for different values of asynchronicity parameter $f=\Omega _\star /\Omega$.

Figure 4: Extra energy $\Delta E$ (in units of $A^2\Omega ^2$) needed for a particle leaving $L_1^{\rm rot}$ to reach the L1 point, plotted vs. asynchronicity parameter $f=\Omega _\star /\Omega$ for values of binary mass ratio of q=0.1 and q=1. Dash-pointed line shows value $\Delta E=0$. The inserted panel shows the dependence of $\Delta E$ vs. f for large values of f.

This is illustrated in Fig. 2 which shows the equatorial plane of a binary with q=1. The isoline of the Roche potential $\Phi$ passing through L₁ (i.e. the XY projection of the classical Roche limit) is shown by a dashed line, while the isoline of potential $\Psi$, passing through $L_1^{\rm rot}$, is drawn by a solid line. The "asynchronous Roche lobes'' are shown for three values of "asynchronicity'' parameter: f=2, f=10, and f=100 (see panels a), b), and c) of Fig. 2, respectively). The vectors of linear velocity of $L_1^{\rm rot}$ point ( ${\vec V}_{\rm rot}=({\vec\Omega}_\star-{\vec\Omega})\times{\vec r}_{L_1^{\rm rot}}$) in the adopted coordinate system are also shown.

Figure 5a: Top panel: bird's-eye view of density isosurfaces on level $\rho =5\times 10^{-5}\cdot \rho (L_1^{\rm rot})$ for the moment of time $t=0.514P_{\rm orb}$. Middle panel: the slice of formed envelope by XY plane (density distribution and velocity vectors in equatorial plane). Vector in top right corner corresponds to velocity 500 km s-1. Bottom panel: the slice of the envelope by XZ (density distribution in frontal plane). Coordinates in all three panels are expressed in $R_\odot$.

Figure 5b: The same as Fig. 5a but for the time $t=0.545P_{\rm orb}$.

Figure 5c: The same as Fig. 5a but for the time $t=0.586P_{\rm orb}$.

Figure 5d: The same as Fig. 5a but for the time $t=0.608P_{\rm orb}$.

Figure 5e: The same as Fig. 5a but for the time $t=0.639P_{\rm orb}$.

Figure 5f: The same as Fig. 5a but for the time $t=0.660P_{\rm orb}$.

As discussed above, the matter can outflow from the stellar surface as it reaches $L_1^{\rm rot}$ point. This fact changes the limiting value of the break-up velocity when the outflow begins. In Fig. 3, the values of the linear velocity at $L_1^{\rm rot}$ point are plotted as a function of binary mass ratio q for different values of asynchronicity parameter f. All velocities are expressed in the units of the critical velocity $V_{\rm br}$, derived for a single star of the same properties. The results presented in Fig. 3 show that in a number of cases even a small additional increase in the rotational velocity can lead to an outflow of matter in the vicinity of $L_1^{\rm rot}$ point. However, for values typical for Be stars, say $q\sim0.1$ and $f\sim100$, the outflow occurs for rotational velocities only slightly smaller than the break-up velocity of the respective star. It is important to realize, however, that when  $V_{\rm rot}$ gets close to $V_{\rm br}$ for Be stars, which are members of binary systems, the outflow of matter occurs only in the vicinity of $L_1^{\rm rot}$, not from the the whole equatorial belt of the star (the Roche limit for single stars).

The presence of a companion to the Be star results in another notable change in the mechanism of the outflow from the surface of a rotating star. For a single star, a particle can escape to infinity if it has the parabolic velocity. For a binary star, the particle leaving via $L_1^{\rm rot}$ point can escape from the system if its energy is large enough to reach the L₁ point (this energy is smaller than that needed to reach the escape velocity from a single star) since after it reaches L₁, it can be captured by the gravitational field of the companion. Particles with energies insufficient to reach the L₁ point will move along closed trajectories around the star from which they escaped. The extra energy $\Delta E$, needed to get a particle with velocity $V_{\rm rot}=(\Omega_\star-\Omega)\cdot x_{L_1^{\rm rot}}$ to the vicinity of L₁ point, is plotted in Fig. 4 as a function of f for two mass ratios, q=1 and q=0.1, and is expressed in the units of the characteristic energy of the system $E_{\rm sys}=A^2\Omega^2$. It is obvious that the sum of potential energy of a particle in  $L_1^{\rm rot}$ point plus its kinetic energy given by the stellar rotation is much smaller than the potential energy in L₁ point

$$\Phi(L_1^{\rm rot})+\hbox{$~^{1}\!/_{2}$ }(\Omega_\star-\Omega)^2\cdot x_{L_1^{\rm rot}}^2< \Phi(L_1).$$

The value of extra energy needed to reach L₁ is a few orders of magnitude larger than the characteristic energy of the system $E_{\rm sys}$. Considering that the effective temperatures of B stars range roughly from 10 000 to 30 000 K, it is clear that the thermal energy cannot change the overall energy balance significantly. One is, therefore, led to the conclusion that the outlow from rapidly rotating B stars in binaries via the $L_1^{\rm rot}$ point should lead to the formation of roughly Keplerian equatorial disks around such stars but not to a significant mass transfer towards their companions.

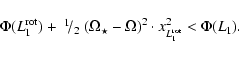
It is necessary to point out, however, that the above analysis of the energy balance is not exhaustive. For instance, the numerical investigations carried out by Narita et al. (1994) show that if the rotational velocity is close to $V_{\rm br}$ and viscosity is considered, a disk in a binary system may evolve from an accretion disk to an outflowing one. At the same time, their numerical simulations showed that the transfer of the angular momentum is far more pronounced than the mass loss and that the mass loss by the disk is significant only on the evolutionary time scale (i.e. $\sim$10⁶ years). Unfortunately, it is impossible to carry out 3-D gas-dynamical simulations for such long time intervals with present-day computers. One only has to expect that a viscous smearing will not significantly influence the solution obtained only over a time interval comparable to the orbital period of the binary (say, less than a year).

It summary, the outlow of matter via the $L_1^{\rm rot}$ point seems to represent the most probable scenario of the formation of the Be envelope for a rapidly rotating B star which is a member of a binary system.