Features appearing in the 10 ![]() m band can be associated directly with changes in the Si-O
bonding state and in particular with SiOn structural units. It is partly for this reason
that both laboratory investigators and astronomers have tended to concentrate on the analysis of
the 10
m band can be associated directly with changes in the Si-O
bonding state and in particular with SiOn structural units. It is partly for this reason
that both laboratory investigators and astronomers have tended to concentrate on the analysis of
the 10 ![]() m band. However, as this paper compares spectral evolution with long-range structural
evolution, it will prove instructive in the present instance to consider the evolution of the
20
m band. However, as this paper compares spectral evolution with long-range structural
evolution, it will prove instructive in the present instance to consider the evolution of the
20 ![]() m band first.
m band first.
Annealing for 4 hours at 873 K produced three broad 20 ![]() m band features which became more
pronounced by 933 K, splitting into four features at 970 K with numerous minor additional
fine-structure features appearing at 1000 K. At each of the lower temperatures the IR features
appear to be insensitive to annealing time, with spectra showing little variation between the
short and long annealing periods used in the experiment.
m band features which became more
pronounced by 933 K, splitting into four features at 970 K with numerous minor additional
fine-structure features appearing at 1000 K. At each of the lower temperatures the IR features
appear to be insensitive to annealing time, with spectra showing little variation between the
short and long annealing periods used in the experiment.
Originating generally in the vibrational modes associated with the inter-tetrahedral bend,
changes in the morphology of this band are accepted as markers for changes occurring in the
longer-range silicate network arrangement (Nuth & Hecht 1990). Although no direct correlation
exists between the specific spectral components in this band and any physical parameters
specifically related to the longer-range structure of silicates, such as the number of
inter-linked tetrahedra etc. (McMillan 1984a, 1984b), the formation of fine structure in this
band can be taken as indicating that the overall silicate structure does indeed evolve as a
function of annealing temperature. With the exception of the 11.2 ![]() m feature, the 20
m feature, the 20 ![]() m
band features appeared to form earlier than those at 10
m
band features appeared to form earlier than those at 10 ![]() m and had quickly stabilised during
the shorter annealing times. This behaviour mirrors that seen in the XRD data, which showed
long-range crystal growth stabilising over a similar time scale and did not appear to evolve
further with annealing time.
m and had quickly stabilised during
the shorter annealing times. This behaviour mirrors that seen in the XRD data, which showed
long-range crystal growth stabilising over a similar time scale and did not appear to evolve
further with annealing time.
Jäger et al. (1998) have published peak positions for several Mg-rich crystalline olivine
(forsterite) and pyroxene (clino- and ortho-enstatite) minerals (taken from transmission
measurements without background correction). For the three 20 ![]() m band features seen in our
933 K spectra, where they are most developed, at 19.7, 21.5 and 23.7
m band features seen in our
933 K spectra, where they are most developed, at 19.7, 21.5 and 23.7 ![]() m, the Mg-rich
pyroxene data of Jäger et al. lists peaks at 19.3, 21.6 and 23.2
m, the Mg-rich
pyroxene data of Jäger et al. lists peaks at 19.3, 21.6 and 23.2 ![]() m while their synthetic
forsterite data shows peaks at 19.5, 21.5 and 23.5
m while their synthetic
forsterite data shows peaks at 19.5, 21.5 and 23.5 ![]() m. Overall the three peaks in our 20
m. Overall the three peaks in our 20 ![]() m band data appear to be represented quite well by Jäger et al.'s Mg-rich forsterite
figures. Considering now our 970 K spectra, the four features peak at 19.7, 20.9, 21.6 and 23.8
m band data appear to be represented quite well by Jäger et al.'s Mg-rich forsterite
figures. Considering now our 970 K spectra, the four features peak at 19.7, 20.9, 21.6 and 23.8 ![]() m, compared to the Jäger et al. pyroxene values of 19.3, 20.6, 21.6 and 23.2
m, compared to the Jäger et al. pyroxene values of 19.3, 20.6, 21.6 and 23.2 ![]() m and
synthetic forsterite values 19.5, 20.8, 21.5 and 23.5
m and
synthetic forsterite values 19.5, 20.8, 21.5 and 23.5 ![]() m. Again our data is best represented
by forsterite. The assignment of these features to forsteritic olivine matches the identification
of the crystallite by the XRD analysis. Interestingly, Jäger et al. attribute the forsterite
vibrations at 19.5
m. Again our data is best represented
by forsterite. The assignment of these features to forsteritic olivine matches the identification
of the crystallite by the XRD analysis. Interestingly, Jäger et al. attribute the forsterite
vibrations at 19.5 ![]() m to the symmetric inter-tetrahedral bend, the 20.8 and 21.5
m to the symmetric inter-tetrahedral bend, the 20.8 and 21.5 ![]() m
features to SiO4 rotation and their 23.5
m
features to SiO4 rotation and their 23.5 ![]() m feature to the translational vibration of a
Me2+ metal ion. This last feature is the one that appears to differ most between their
pyroxene and olivine samples. Jäger et al. note it as being stronger in olivine than pyroxene
as well as located at different wavelengths for different Fe content and mineral type. In our
data this feature appears to be the 20
m feature to the translational vibration of a
Me2+ metal ion. This last feature is the one that appears to differ most between their
pyroxene and olivine samples. Jäger et al. note it as being stronger in olivine than pyroxene
as well as located at different wavelengths for different Fe content and mineral type. In our
data this feature appears to be the 20 ![]() m band feature to develop first in both strength and
narrowness. It is likely that the ionic translational freedom will be strongly influenced by its
local molecular co-ordination and hence the feature will strongly reflect the surrounding
crystal symmetry. The presence of this feature, in combination with the 11.2
m band feature to develop first in both strength and
narrowness. It is likely that the ionic translational freedom will be strongly influenced by its
local molecular co-ordination and hence the feature will strongly reflect the surrounding
crystal symmetry. The presence of this feature, in combination with the 11.2 ![]() m feature (see
below), is likely therefore to be a strong diagnostic for the presence of a forsteritic
structure.
m feature (see
below), is likely therefore to be a strong diagnostic for the presence of a forsteritic
structure.
Unprocessed, our sample showed a shoulder at ![]() 11.2
11.2 ![]() m which formed a feature after 4
hours annealing at 873 K. At this temperature the overall 10
m which formed a feature after 4
hours annealing at 873 K. At this temperature the overall 10 ![]() m band morphology had changed
little with respect to the unprocessed sample. At 933 K further features and shoulders formed,
continuing to grow at 970 K and 1000 K. Overall this band appeared more sensitive to annealing
than the 20
m band morphology had changed
little with respect to the unprocessed sample. At 933 K further features and shoulders formed,
continuing to grow at 970 K and 1000 K. Overall this band appeared more sensitive to annealing
than the 20 ![]() m band. It has long been known that spectral components within this band can be
identified which correlate directly with tetrahedral species with differing numbers of NBO
atoms (Nuth & Hecht 1990) and can in principle be used to determine the relative proportions of
network, sheet, chain, dimer and independent tetrahedral units present in the silicate
(Thompson 1996). Features within the 10
m band. It has long been known that spectral components within this band can be
identified which correlate directly with tetrahedral species with differing numbers of NBO
atoms (Nuth & Hecht 1990) and can in principle be used to determine the relative proportions of
network, sheet, chain, dimer and independent tetrahedral units present in the silicate
(Thompson 1996). Features within the 10 ![]() m band originate in the Si-O fundamental
stretch mode which is strongly influenced by whether the oxygen is a bridging or non-bridging
atom. Lack of variation of the 10
m band originate in the Si-O fundamental
stretch mode which is strongly influenced by whether the oxygen is a bridging or non-bridging
atom. Lack of variation of the 10 ![]() m band peak intensity and shape relative to the 20
m band peak intensity and shape relative to the 20 ![]() m
band in amorphous systems, has previously been taken as evidence that the features within the
10
m
band in amorphous systems, has previously been taken as evidence that the features within the
10 ![]() m band are insensitive to the longer-range structure of the silicate (McMillan 1984a, 1984b).
The fact that our data shows band features that vary with both time and temperature
suggests that during annealing the short-range local tetrahedral environment evolves without
necessarily impinging on the longer-range inter-tetrahedral network structure. At present we
are unable to comment on whether the changes in the 10
m band are insensitive to the longer-range structure of the silicate (McMillan 1984a, 1984b).
The fact that our data shows band features that vary with both time and temperature
suggests that during annealing the short-range local tetrahedral environment evolves without
necessarily impinging on the longer-range inter-tetrahedral network structure. At present we
are unable to comment on whether the changes in the 10 ![]() m band are precursors to eventual
change in the 20
m band are precursors to eventual
change in the 20 ![]() m band or whether the 10
m band or whether the 10 ![]() m band evolution represents the short-range
environment adapting to the imposition of long-range structure.
m band evolution represents the short-range
environment adapting to the imposition of long-range structure.
The stability of both the 20 ![]() m band features and long-range XRD data suggests that any
physical changes associated with variations observed in the 10
m band features and long-range XRD data suggests that any
physical changes associated with variations observed in the 10 ![]() m band do not impinge on the
silicate network structure, although this last statement needs some qualification. From the XRD
measurements we can determine two limiting lengths. The first is the smallest real-space
separation we are able to resolve using X-rays. For any angle dispersive diffraction experiment
performed at a given X-ray wavelength the k-space maximum is determined by the maximum
scattering angle,
m band do not impinge on the
silicate network structure, although this last statement needs some qualification. From the XRD
measurements we can determine two limiting lengths. The first is the smallest real-space
separation we are able to resolve using X-rays. For any angle dispersive diffraction experiment
performed at a given X-ray wavelength the k-space maximum is determined by the maximum
scattering angle,
![]() ,
and in turn corresponds to a minimum real-space distance
below which we can not probe,
,
and in turn corresponds to a minimum real-space distance
below which we can not probe,
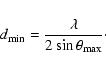 |
(4) |
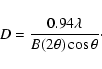 |
(5) |
Within the experimental noise inherent in the counting statistics the crystallite appears to
show no systematic growth with annealing time, although the diffraction peak intensities, when
corrected for synchrotron beam decay do show an initial increase with annealing time for the
first few scans, which we interpret as being due to the initial formation of crystalline
structure (possibly localised). The lack of subsequent growth can be interpreted in several ways,
either as a stall in the physical extent of crystalline development within the sample particles
(since the reflection widths show no systematic decrease with annealing time, suggesting the
number of participating layers is constant), or a stall in the total number of crystallites
(since the peak intensities do not increase). This latter could be due either to the number of
crystallite nucleation centres being fixed during sample manufacture, with no new centres forming
during annealing, or to the physical properties of the sample particles. In preparing our sample
for presentation to the synchrotron beam, the particle size distribution was not tightly
constrained. The sample powder was ground by hand in a pestle and mortar, which does not produce
a monotonic grain size distribution (as evidenced by SEM). From our present data we are unable to
address the question as to what extent the thermodynamic contribution of particle surface area
affects the crystallisation process. It is also difficult to tell from either the XRD or SEM data
whether the crystallite size, D, represents a whole particle size (in which case only the
smallest particles would appear to have crystallised), or whether it represents either the size
of crystalline "inclusions'' within otherwise amorphous particles, or a crystallite domain size
within fully crystallised particles. If D does represent the whole crystalline particle size,
we would have expected a systematic increase in its value with integrated annealing time as
grinding of the sample produced a range of grain sizes which we would expect to have successively
succumbed to crystallisation as annealing progressed. Furthermore, the overall initial change in
the amorphous component of the diffraction patterns at 1000 K (e.g. narrowing of the diffuse
diffraction features relative to those in the unprocessed sample) clearly indicates that
structural change does occur throughout all our sample (remember X-ray diffraction represents an
average snapshot of the bulk whole-sample structure). Since crystallisation only occurs in an
amorphous material at the expense of its amorphousness, it is unlikely that such apparent changes
would be confined to only the very smallest particles and still show up in the diffraction
patterns. Additionally, Hallenbeck et al. (1998) interpreted the formation of an Si-O stretching
band morphology with well defined features near 9.8 ![]() m and 11.2
m and 11.2 ![]() m as a natural
consequence of the thermal evolution of amorphous silicates, rather than arising from a distinct
mixture of amorphous and crystalline materials.
m as a natural
consequence of the thermal evolution of amorphous silicates, rather than arising from a distinct
mixture of amorphous and crystalline materials.
From the foregoing arguments, it would appear that the physical changes occurring within the
silicate that give rise to some of the 10 ![]() m band fine structure do not correlate
with the observed crystalline evolution as defined within the limits of the minimum X-ray
resolution or the crystallite correlation length.
m band fine structure do not correlate
with the observed crystalline evolution as defined within the limits of the minimum X-ray
resolution or the crystallite correlation length.
The feature at ![]() 11.2
11.2 ![]() m, initially present in the unprocessed amorphous sample as a
shoulder is the first feature to develop as a peak in the 10
m, initially present in the unprocessed amorphous sample as a
shoulder is the first feature to develop as a peak in the 10 ![]() m region in terms of both
annealing temperature and exposure time. At the lowest annealing temperature of 873 K and 4 hours
exposure it appears to develop as an obvious peak while the three 20
m region in terms of both
annealing temperature and exposure time. At the lowest annealing temperature of 873 K and 4 hours
exposure it appears to develop as an obvious peak while the three 20 ![]() m features are still
somewhat broad and poorly defined. Commonly attributed to the Si-O stretch for SiO4 species,
its strength appears to grow in association with the 20
m features are still
somewhat broad and poorly defined. Commonly attributed to the Si-O stretch for SiO4 species,
its strength appears to grow in association with the 20 ![]() m features as both annealing time
and temperature increase. As we have identified the 20
m features as both annealing time
and temperature increase. As we have identified the 20 ![]() m features with forsteritic olivine
(and in particular the 23.8
m features with forsteritic olivine
(and in particular the 23.8 ![]() m feature) the association of the 11.2
m feature) the association of the 11.2 ![]() m feature with
forsterite appears to be confirmed along with the correlation of its strength with the formation
of crystalline structure.
m feature with
forsterite appears to be confirmed along with the correlation of its strength with the formation
of crystalline structure.
The development of a feature at ![]() 9.3
9.3 ![]() m in the data from 970 K onwards is also
interesting. Although Jäger et al. (1998) identify the presence of a feature at this position in
synthetic 100% Mg forsterite (which in their data disappears with increasing Fe content), the
presence of a feature at 9.3
m in the data from 970 K onwards is also
interesting. Although Jäger et al. (1998) identify the presence of a feature at this position in
synthetic 100% Mg forsterite (which in their data disappears with increasing Fe content), the
presence of a feature at 9.3 ![]() m is more commonly attributed to crystalline pyroxene spectra
(e.g. Koike et al. 1981, 1993; Jäger et al. 1998; Brucato et al. 1999b). Observations of Comet
Hale-Bopp by Wooden et al. (1999) have shown the presence of a 9.3
m is more commonly attributed to crystalline pyroxene spectra
(e.g. Koike et al. 1981, 1993; Jäger et al. 1998; Brucato et al. 1999b). Observations of Comet
Hale-Bopp by Wooden et al. (1999) have shown the presence of a 9.3 ![]() m feature that increases
in strength as the comet approaches perihelion. The development of this feature in the comet
spectra is also accompanied by the development of three weak features at 10.5, 10.8 and 11.8
m feature that increases
in strength as the comet approaches perihelion. The development of this feature in the comet
spectra is also accompanied by the development of three weak features at 10.5, 10.8 and 11.8
![]() m which are also present in our data. Grains with pyroxene compositions are implied by the
PUMA-1 results (Jessberger et al. 1988; Lawler et al. 1989) for Comet Halley and differences
between the 10
m which are also present in our data. Grains with pyroxene compositions are implied by the
PUMA-1 results (Jessberger et al. 1988; Lawler et al. 1989) for Comet Halley and differences
between the 10 ![]() m bands for various comets have previously been attributed (at least in part)
to variations in the relative abundance of crystalline/amorphous olivines and amorphous pyroxenes
(as well as to the Mg:Fe ratio). Amorphous pyroxene grains have been invoked to explain the
short-wavelength rise of the 10
m bands for various comets have previously been attributed (at least in part)
to variations in the relative abundance of crystalline/amorphous olivines and amorphous pyroxenes
(as well as to the Mg:Fe ratio). Amorphous pyroxene grains have been invoked to explain the
short-wavelength rise of the 10 ![]() m band as well as the 9.8
m band as well as the 9.8 ![]() m peak, for example in Comet
Halley (e.g. Hanner et al. 1994b; Colangeli et al. 1995). Despite this, and the identification of
Mg-rich pyroxenes in certain types of interplanetary dust particles (Bradley et al. 1997), the
presence of crystalline pyroxene has not been inferred from the 10
m peak, for example in Comet
Halley (e.g. Hanner et al. 1994b; Colangeli et al. 1995). Despite this, and the identification of
Mg-rich pyroxenes in certain types of interplanetary dust particles (Bradley et al. 1997), the
presence of crystalline pyroxene has not been inferred from the 10 ![]() m band spectra of comets
prior to Hale-Bopp (Wooden et al. 1999). At 2.8 AU Wooden et al. observed the 10
m band spectra of comets
prior to Hale-Bopp (Wooden et al. 1999). At 2.8 AU Wooden et al. observed the 10 ![]() m band of
Hale-Bopp to be similar to Halley's and fitted its spectra with a three component mineral
mixture: amorphous olivine with 50% Mg (relative to Fe), crystalline olivine with 90% Mg and
amorphous pyroxene with 100% Mg. At 1.7 AU they report the presence of a 9.3
m band of
Hale-Bopp to be similar to Halley's and fitted its spectra with a three component mineral
mixture: amorphous olivine with 50% Mg (relative to Fe), crystalline olivine with 90% Mg and
amorphous pyroxene with 100% Mg. At 1.7 AU they report the presence of a 9.3 ![]() m peak along
with the three features at 10.5, 10.8 and 11.8
m peak along
with the three features at 10.5, 10.8 and 11.8 ![]() m and suggest the evolution of such features
at short heliocentric distances to be due to the addition of a fourth mineral phase, obtaining a
fit at 9.3
m and suggest the evolution of such features
at short heliocentric distances to be due to the addition of a fourth mineral phase, obtaining a
fit at 9.3 ![]() m using crystalline pyroxene with a Mg content
m using crystalline pyroxene with a Mg content ![]() .
To explain the
non-appearance of this extra crystalline phase at greater distances they suggest that the high Mg content of crystalline pyroxene makes its grains less optically active and therefore cooler
than Mg-rich olivine grains. An alternative possibility for the 9.3
.
To explain the
non-appearance of this extra crystalline phase at greater distances they suggest that the high Mg content of crystalline pyroxene makes its grains less optically active and therefore cooler
than Mg-rich olivine grains. An alternative possibility for the 9.3 ![]() m feature carrier could
be a pure, amorphous SiOn such as SiO2 or Si2O3 which have peak absorbances
near 9.2-9.3
m feature carrier could
be a pure, amorphous SiOn such as SiO2 or Si2O3 which have peak absorbances
near 9.2-9.3 ![]() m. These should also be accompanied by other features such as a shoulder at
m. These should also be accompanied by other features such as a shoulder at
![]() 8.4
8.4 ![]() m and a peak at 11.4
m and a peak at 11.4 ![]() m for Si2O3 and a peak at
m for Si2O3 and a peak at ![]() 12.5
12.5 ![]() m
for SiO2. However inspection of our spectra does not reveal the presence of these additional
features. As a note of caution however, we draw attention to the fact that the current literature
relating to laboratory silicate analogues presents results obtained from samples manufactured by
a variety of methods. Thus there is a large question concerning the parity between the various
results, as well as how well the various samples adequately model real cosmic silicates. Samples
produced as condensates of Mg and SiO vapours not only tend to lack many full SiO4 tetrahedra, but will also contain free silica, MgO oxides and Mg metal. Such samples
are therefore (in terms of silicate) highly disordered both structurally and chemically. Samples
produced by laser ablation of mineral specimen will contain condensed, non-crystalline particles
as well as liquid drops and solid spall from the target. Gel desiccation on the other hand
tends to produce silicates that are chemically well defined with a well established, but disordered,
tetrahedral environment. The samples produced by each of these techniques are in turn also
dependent on the precise details governing the manufacturing processes involved. These
differences of production can ultimately lead to a difference in physical behaviour. As noted
previously (Thompson & Tang 2001), samples such as vapour condensed silicate may require
substatially higher annealing temperatures in order to crystallise. However cometary grains
are likely to have suffered post-formation processing in stellar atmospheres, the interstellar
medium and pre-solar nebular prior to incorporation into comet bodies and thus may not be best
modelled by samples more representative of freshly nucleated dust grains. Therefore, whilst we
acknowledge the method of manufacture of our initial silicate might yield a somewhat idealised
analogue to comet dust, it should be borne in mind that the validity of fitting
observed spectra with laboratory data obtained from fully crystalline materials does rely
explicitly on the underlying assumption that such features can be definitively
attributed to crystalline grain components with certain macroscopic structures.
That we have found, using two complimentary techniques, that a sample of amorphous pyroxene
composition can crystallise to a forsterite structure and still display certain pyroxene-like
fine-structure features does at the very least open up the possibility that certain of the
features seen in the 10
m
for SiO2. However inspection of our spectra does not reveal the presence of these additional
features. As a note of caution however, we draw attention to the fact that the current literature
relating to laboratory silicate analogues presents results obtained from samples manufactured by
a variety of methods. Thus there is a large question concerning the parity between the various
results, as well as how well the various samples adequately model real cosmic silicates. Samples
produced as condensates of Mg and SiO vapours not only tend to lack many full SiO4 tetrahedra, but will also contain free silica, MgO oxides and Mg metal. Such samples
are therefore (in terms of silicate) highly disordered both structurally and chemically. Samples
produced by laser ablation of mineral specimen will contain condensed, non-crystalline particles
as well as liquid drops and solid spall from the target. Gel desiccation on the other hand
tends to produce silicates that are chemically well defined with a well established, but disordered,
tetrahedral environment. The samples produced by each of these techniques are in turn also
dependent on the precise details governing the manufacturing processes involved. These
differences of production can ultimately lead to a difference in physical behaviour. As noted
previously (Thompson & Tang 2001), samples such as vapour condensed silicate may require
substatially higher annealing temperatures in order to crystallise. However cometary grains
are likely to have suffered post-formation processing in stellar atmospheres, the interstellar
medium and pre-solar nebular prior to incorporation into comet bodies and thus may not be best
modelled by samples more representative of freshly nucleated dust grains. Therefore, whilst we
acknowledge the method of manufacture of our initial silicate might yield a somewhat idealised
analogue to comet dust, it should be borne in mind that the validity of fitting
observed spectra with laboratory data obtained from fully crystalline materials does rely
explicitly on the underlying assumption that such features can be definitively
attributed to crystalline grain components with certain macroscopic structures.
That we have found, using two complimentary techniques, that a sample of amorphous pyroxene
composition can crystallise to a forsterite structure and still display certain pyroxene-like
fine-structure features does at the very least open up the possibility that certain of the
features seen in the 10 ![]() m band of objects such as comets might not correlate directly with
the macroscopic crystalline grain structure. After all, the features in this region are generally
accepted as being independent of the material's long-range structure. In such instances, fits to
pyroxene-like features in the 10
m band of objects such as comets might not correlate directly with
the macroscopic crystalline grain structure. After all, the features in this region are generally
accepted as being independent of the material's long-range structure. In such instances, fits to
pyroxene-like features in the 10 ![]() m band would have to be constrained by the spectral
behaviour at other wavelengths before necessarily being accepted as definitive. In the case of
Hale-Bopp, features seen at longer wavelengths (19.5, 23.5 and 33.5
m band would have to be constrained by the spectral
behaviour at other wavelengths before necessarily being accepted as definitive. In the case of
Hale-Bopp, features seen at longer wavelengths (19.5, 23.5 and 33.5 ![]() m) at pre-perihelion
distances have already been identified with forsterite (Crovisier et al. 1997). Presumably the
appearance of crystalline pyroxene grains at perihelion should also be detectable at longer
wavelengths.
m) at pre-perihelion
distances have already been identified with forsterite (Crovisier et al. 1997). Presumably the
appearance of crystalline pyroxene grains at perihelion should also be detectable at longer
wavelengths.
There are several possible plausible explanations for the presence of these "crystalline''
enstatite features in a crystalline forsterite dominated sample. Firstly, given the absence of
enstatite features in the diffraction data, they could originate from micro-crystalline enstatite
structures, too small to be detected using our current diffraction apparatus, or they could
represent an ultra dilute phase whose presence would require much greater detector integration
times to detect than those employed in our measurements. In both cases, this would imply a 10
![]() m spectral response for enstatite that is very strong in relation to its physical extent
(and also relative to forsterite) and presumably a 20
m spectral response for enstatite that is very strong in relation to its physical extent
(and also relative to forsterite) and presumably a 20 ![]() m response that is correspondingly
weaker so as not to be visible in this band. IR spectroscopy only returns information regarding
the average bond type. Thus, while there may be sufficient "enstatite'' Si-O bonds to produce
features in the 10
m response that is correspondingly
weaker so as not to be visible in this band. IR spectroscopy only returns information regarding
the average bond type. Thus, while there may be sufficient "enstatite'' Si-O bonds to produce
features in the 10 ![]() m band, to produce features in the 20
m band, to produce features in the 20 ![]() m band would require these to
be arranged in an enstatite lattice, which is clearly not the case. A more realistic possibility
could be that these features represent an improvement in the local SiO3 ordering arising as
a result of annealing, but without the formation of regular crystallographic structure. Such
changes for example could result from wide-spread, but highly localised, changes (e.g. changes in
polymerisation) that do not repeat in a regular way over macroscopic lengths, or could represent
changes in the inter-linked tetrahedral environment that are not reliant on any one particular
macroscopic structural arrangement being adopted. As such the appearance of these
pre-crystalline enstatite features in observed spectra may only signal that the silicate has been
annealed, rather than actually tell us something about the macroscopic structure of the material
itself. It is therefore worth stressing that this finding could potentially offer new
perspectives on the reconstruction of the thermal history of comets, even if at this stage it is
deserving of more detailed study.
m band would require these to
be arranged in an enstatite lattice, which is clearly not the case. A more realistic possibility
could be that these features represent an improvement in the local SiO3 ordering arising as
a result of annealing, but without the formation of regular crystallographic structure. Such
changes for example could result from wide-spread, but highly localised, changes (e.g. changes in
polymerisation) that do not repeat in a regular way over macroscopic lengths, or could represent
changes in the inter-linked tetrahedral environment that are not reliant on any one particular
macroscopic structural arrangement being adopted. As such the appearance of these
pre-crystalline enstatite features in observed spectra may only signal that the silicate has been
annealed, rather than actually tell us something about the macroscopic structure of the material
itself. It is therefore worth stressing that this finding could potentially offer new
perspectives on the reconstruction of the thermal history of comets, even if at this stage it is
deserving of more detailed study.
Previously reported XRD annealing results (Thompson & Tang 2001) show the forsterite structure formed in this MgSiO3 powder persists as the prominent crystal phase at least up to 1173 K, whether further annealing at this, or higher, temperatures would eventually produce a phase change resulting in the expected enstatite pyroxene structure is currently unknown. The formation of macroscopic crystalline pyroxene structures from amorphous grains could in fact be harder to realise than their composition alone suggests.
Copyright ESO 2002