As a starting point in this work we have chosen an amorphous silicate manufactured so as to have
the same stoichiometry as the Mg-rich pyroxene end member enstatite. We shall in time be
broadening the scope of our experiments to include other silicate compositions (including iron
silicates) and will report the results of these investigations in subsequent papers. Estimates of
the Mg/Si ratio for Comet Halley, obtained from the PUMA-1 mass spectrometer on board the Vega-1
spacecraft, suggest a value between ![]() 0.5 and
0.5 and ![]() 1.6 (Jessberger et al. 1988;
Lawler et al. 1989). The choice of amorphous MgSiO3 as a starting material is therefore broadly
typical of the type of composition that may be expected in many comets.
1.6 (Jessberger et al. 1988;
Lawler et al. 1989). The choice of amorphous MgSiO3 as a starting material is therefore broadly
typical of the type of composition that may be expected in many comets.
The silicate sample used in these experiments was produced using the well known gel desiccation method (Sabatier 1950; Day 1974) according to the following prescription:
| (1) | |||
To prepare the sample for presentation to both the synchrotron beam and IR spectrometer, the
raw silicate was ground by hand in a mortar and pestle to give a fine-grained powder. SEM
micrographs showed the particles to be typically ![]() 100
100 ![]() m with some as large as several
hundreds of microns, while a limited number of particles also occupy the range from a few microns
to a few tens of microns. Despite observing a substantial mass reduction during annealing, the
SEM data showed no evidence of a change in particle size between processed and unprocessed
samples. This method of preparation does produce particles that are rather large in
comparison to the size of the cometary grains supposed to be responsible for the bands observed
in the 10-20
m with some as large as several
hundreds of microns, while a limited number of particles also occupy the range from a few microns
to a few tens of microns. Despite observing a substantial mass reduction during annealing, the
SEM data showed no evidence of a change in particle size between processed and unprocessed
samples. This method of preparation does produce particles that are rather large in
comparison to the size of the cometary grains supposed to be responsible for the bands observed
in the 10-20 ![]() m spectra of such bodies (Brucato et al. 1999a). However, we think this
difference is not of primary importance for the scope of the present work. Although
Rietmeijer et al. (2002) have observed a size dependency in the annealing behaviour of silicate smokes, the
particle sizes involved their experiments were significantly smaller than in the work discussed
here. We believe therefore that the structural changes discussed in this paper are unlikely to be
strongly dependent on particle size. However, we acknowledge that this point is deserving of
further attention and we plan to investigate this possibility in future experiments.
m spectra of such bodies (Brucato et al. 1999a). However, we think this
difference is not of primary importance for the scope of the present work. Although
Rietmeijer et al. (2002) have observed a size dependency in the annealing behaviour of silicate smokes, the
particle sizes involved their experiments were significantly smaller than in the work discussed
here. We believe therefore that the structural changes discussed in this paper are unlikely to be
strongly dependent on particle size. However, we acknowledge that this point is deserving of
further attention and we plan to investigate this possibility in future experiments.
Based on the parallel beam optics of Parrish et al. (1986), the Daresbury Laboratory synchrotron
radiation source (srs) station 2.3 diffractometer used in our experiment was originally
constructed for ambient high-resolution powder diffraction studies (Cernik et al. 1990;
Collins et al. 1992). Located 15 m tangentially from a 1.2 T dipole magnet in the 2 GeV electron
storage ring (Munro 1997), it receives X-rays in the range 0.7-2.5 Å. These are filtered by a
water cooled Si(111) channel-cut single crystal to give a monochromatic beam incident at the
centre of the two circle (![]() and 2
and 2![]() )
diffractometer. The sample furnace used in the
diffraction experiment is mounted on the diffractometer's
)
diffractometer. The sample furnace used in the
diffraction experiment is mounted on the diffractometer's ![]() -circle with a flat-plate
sample holder inside the device coincident with the centre of the
-circle with a flat-plate
sample holder inside the device coincident with the centre of the ![]() -circle allowing
Hart-Parrish diffraction geometry to be achieved (Hart & Parrish 1986). This makes the diffraction
optics insensitive to changes in sample height, which is essential as small movements are
inevitable when the sample is heated. The whole furnace assembly is enclosed in a stainless steel
body, with incident and diffracted X-rays passing through kapton entrance and exit windows
allowing measurements to be made during annealing. The diffracted beam passes through a parallel
foil assembly on the 2
-circle allowing
Hart-Parrish diffraction geometry to be achieved (Hart & Parrish 1986). This makes the diffraction
optics insensitive to changes in sample height, which is essential as small movements are
inevitable when the sample is heated. The whole furnace assembly is enclosed in a stainless steel
body, with incident and diffracted X-rays passing through kapton entrance and exit windows
allowing measurements to be made during annealing. The diffracted beam passes through a parallel
foil assembly on the 2![]() arm and is detected using an enhanced dynamic range scintillation
counter.
arm and is detected using an enhanced dynamic range scintillation
counter.
The furnace itself is based on a design by Debrenne et al. (1970), details of which are given in
Tang et al. (1998). The sample crucible is made of molybdenum, chosen for its high melting point and
induction characteristics, while a 1 mm deep and 15 mm diameter pressed platinum former is placed
on the crucible to hold the sample and to prevent possible chemical reaction between sample and
crucible at high temperatures. Heating is via a water-cooled 2 kW RF copper coil regulated by a
Eurotherm 900 controller. Sample temperature is measured by a tungsten-rhenium thermocouple
placed at the sample/crucible assembly. The operational temperature range is 290-2000 K with a
heating response time of ![]() 30 s. Even at high temperatures,
30 s. Even at high temperatures, ![]() 1 K stability is achieved in
under a few minutes. In order to ramp our sample up to the 1000 K annealing temperature, the
furnace temperature was increased in steps of
1 K stability is achieved in
under a few minutes. In order to ramp our sample up to the 1000 K annealing temperature, the
furnace temperature was increased in steps of ![]() 200 K over a period of approximately 5 min, with the approach to 1000 K being made in progressively smaller increments to avoid
overshoot of the target temperature. Data collection began as soon as the temperature stabilised
at 1000 K (approximately 2-3 min).
200 K over a period of approximately 5 min, with the approach to 1000 K being made in progressively smaller increments to avoid
overshoot of the target temperature. Data collection began as soon as the temperature stabilised
at 1000 K (approximately 2-3 min).
Normally ![]() -
-![]() XRD patterns are collected by synchronised rotation of the
XRD patterns are collected by synchronised rotation of the
![]() and 2
and 2![]() arms. However to prevent the sample falling from the holder at high
angle, the
arms. However to prevent the sample falling from the holder at high
angle, the ![]() circle was fixed so that the sample was inclined at 10
circle was fixed so that the sample was inclined at 10![]() to the
horizontal incoming beam and the diffraction intensities corrected accordingly. An X-ray
wavelength of 1.2995 Å (calibrated against a Si powder standard) was selected as a good
compromise between peak incident flux and the requirement for low wavelength for increased X-ray
reciprocal wave vector k-space sampling within the silicate. For a given X-ray wavelength,
to the
horizontal incoming beam and the diffraction intensities corrected accordingly. An X-ray
wavelength of 1.2995 Å (calibrated against a Si powder standard) was selected as a good
compromise between peak incident flux and the requirement for low wavelength for increased X-ray
reciprocal wave vector k-space sampling within the silicate. For a given X-ray wavelength,
![]() ,
this is given by
,
this is given by
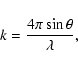 |
(2) |
In order to perform spectroscopic measurements, the samples were prepared according to the standard pellet technique as described by Borghesi et al. (1985) and Bussoletti et al. (1987). The technique is based on the dispersion of a known quantity of sample in an IR transparent matrix (KBr in our case). The resulting mixture is then compressed into a solid pellet and the sample spectrum recovered by comparison with a pellet of pure KBr.
With the obvious exclusion of the unprocessed sample, all the others were annealed in a
Carbolite furnace, model CTF 12/65, capable of reaching a maximum temperature of 1200 ![]() C. The sample compartment consists of an alumina tube approximately 700 mm in length
and 75 mm in diameter, with the sample being placed at the centre of the tube on a small alumina
plate. In addition to the standard furnace thermocouple we placed an additional NiCroSil/NiSil
thermocouple directly in contact with the sample plate so that the annealing temperatures quoted
are, to within a very close approximation, the actual temperatures experienced by each sample.
During annealing, the furnace was evacuated to prevent possible reaction of the hot sample with
atmospheric gases. Annealing began only when the pressure inside the furnace was less than
10-4 mbar. After an initial increase, the pressure remained between
C. The sample compartment consists of an alumina tube approximately 700 mm in length
and 75 mm in diameter, with the sample being placed at the centre of the tube on a small alumina
plate. In addition to the standard furnace thermocouple we placed an additional NiCroSil/NiSil
thermocouple directly in contact with the sample plate so that the annealing temperatures quoted
are, to within a very close approximation, the actual temperatures experienced by each sample.
During annealing, the furnace was evacuated to prevent possible reaction of the hot sample with
atmospheric gases. Annealing began only when the pressure inside the furnace was less than
10-4 mbar. After an initial increase, the pressure remained between
![]() and
and
![]() mbar for most of the time. To further reduce the likelihood of interaction with the
atmosphere, the sample was allowed to cool to ambient temperature before opening the furnace.
Unfortunately the Carbolite furnace has a significant thermal inertia with no cooling system
fitted. The typical annealing profile of the measured temperature at the sample plate as a
function of time is shown in Fig. 1. The furnace is switched on at time t=0 and switched off
at time t3 once the nominal set-point temperature,
mbar for most of the time. To further reduce the likelihood of interaction with the
atmosphere, the sample was allowed to cool to ambient temperature before opening the furnace.
Unfortunately the Carbolite furnace has a significant thermal inertia with no cooling system
fitted. The typical annealing profile of the measured temperature at the sample plate as a
function of time is shown in Fig. 1. The furnace is switched on at time t=0 and switched off
at time t3 once the nominal set-point temperature,
![]() ,
has been maintained for a
required period of time
,
has been maintained for a
required period of time
![]() .
As can be seen from the figure, the rise time
for the temperature is relatively short (between 30 and 45 minutes) depending on the value of
.
As can be seen from the figure, the rise time
for the temperature is relatively short (between 30 and 45 minutes) depending on the value of
![]() ,
whilst the cool-down time to ambient temperature can take more than 24 hours. The
annealing times quoted in this paper therefore have been defined as the interval between the
time t1 at which the furnace reaches 85% of of the target temperature
,
whilst the cool-down time to ambient temperature can take more than 24 hours. The
annealing times quoted in this paper therefore have been defined as the interval between the
time t1 at which the furnace reaches 85% of of the target temperature
![]() (measured
in
(measured
in ![]() C) and the time, t4, when the furnace subsequently cools back down to the same
temperature. We are aware that such a definition may be viewed as somewhat arbitrary and that a
better determination of this important parameter may be desirable. Nevertheless in the present
discussion it can probably be accepted without any major disadvantage for two reasons. Firstly
we have used only two basic annealing times which, in terms of the scope of the present
discussion, can be simply defined as short (from 2 to 4 hours) and long (from 20 to
24 hours). Secondly the data we have obtained appears to depend quite strongly on temperature
while the influence of the annealing time seems to be much weaker.
C) and the time, t4, when the furnace subsequently cools back down to the same
temperature. We are aware that such a definition may be viewed as somewhat arbitrary and that a
better determination of this important parameter may be desirable. Nevertheless in the present
discussion it can probably be accepted without any major disadvantage for two reasons. Firstly
we have used only two basic annealing times which, in terms of the scope of the present
discussion, can be simply defined as short (from 2 to 4 hours) and long (from 20 to
24 hours). Secondly the data we have obtained appears to depend quite strongly on temperature
while the influence of the annealing time seems to be much weaker.
Following removal from the furnace the samples were embedded in KBr, with a pure KBr pellet also
being manufactured at the same time to allow immediate subtraction of the matrix contribution to
be made for spectra collected under similar conditions. The spectra themselves were recorded
using a Spectrum 2000 Perkin-Elmer FT-IR spectrometer. The single beam Michelson
interferometer was equipped, for the spectral range of interest (4000-400 cm-1; 2.5-25 ![]() m), with a KBr beamsplitter, a FR-DTGS (Fast Recovery Deuterated TriGlycine Sulphate)
detector and a wire coil source at 1350 K. A resolution of 4 cm-1 was selected as being
high enough for the convenient detection of solid state absorption features, while the measured
interferograms were directly transformed in spectra using a FFT (Fast Fourier Transform)
algorithm that forms part of the Spectrum for Windows software package supplied by Perkin-Elmer
for operating the whole instrument.
m), with a KBr beamsplitter, a FR-DTGS (Fast Recovery Deuterated TriGlycine Sulphate)
detector and a wire coil source at 1350 K. A resolution of 4 cm-1 was selected as being
high enough for the convenient detection of solid state absorption features, while the measured
interferograms were directly transformed in spectra using a FFT (Fast Fourier Transform)
algorithm that forms part of the Spectrum for Windows software package supplied by Perkin-Elmer
for operating the whole instrument.
Copyright ESO 2002