We observed 12 Galactic globular clusters, 9 of which are located
close to the Milky-Way bulge (see Fig. 1). Four globular
clusters belong to the halo sub-population with a mean metallicity
![]() dex (Harris 1996). The other globular clusters
with higher mean metallicities are associated with the bulge. Our
sample includes the well-studied metal-rich clusters NGC 6553 and NGC
6528, which is located in Baade's Window. Several relevant cluster
properties are summarized in Table 1. Our cluster
sample was selected to maximize the number of high-metallicity
clusters and to ensure a high enough signal-to-noise ratio (S/N) of
the resulting spectra.
dex (Harris 1996). The other globular clusters
with higher mean metallicities are associated with the bulge. Our
sample includes the well-studied metal-rich clusters NGC 6553 and NGC
6528, which is located in Baade's Window. Several relevant cluster
properties are summarized in Table 1. Our cluster
sample was selected to maximize the number of high-metallicity
clusters and to ensure a high enough signal-to-noise ratio (S/N) of
the resulting spectra.
Long-slit spectra were taken on three nights in July 5th to 7th 1999
with the Boller & Chivens Spectrograph of ESO's 1.52 m on La
Silla. We used grating #23 with 600 grooves per mm yielding a
dispersion of 1.89 Å/pix with a spectral range from ![]() 3400 Å to
3400 Å to ![]() 7300 Å. We used the detector CCD #39, a Loral
7300 Å. We used the detector CCD #39, a Loral
![]() pix2 chip, with a pixel size of 15
pix2 chip, with a pixel size of 15 ![]() m and a
scale of 0.82
m and a
scale of 0.82
![]() /pix. Its readout noise is 5.4 e- and the gain
was measured with 1.2 e-/ADU. In order to check the dark current we
also obtained dark images which resulted in a negligible average dark
current of 0.0024 e
/pix. Its readout noise is 5.4 e- and the gain
was measured with 1.2 e-/ADU. In order to check the dark current we
also obtained dark images which resulted in a negligible average dark
current of 0.0024 e
![]() .
The total slit
length of the spectrograph covers 4.5
.
The total slit
length of the spectrograph covers 4.5![]() on the sky. For the
benefit of light sampling the slit width was fixed at 3
on the sky. For the
benefit of light sampling the slit width was fixed at 3
![]() ,
which
guarantees an instrumental resolution (
,
which
guarantees an instrumental resolution (![]() 6.7 Å) which is
smaller than the average resolution (
6.7 Å) which is
smaller than the average resolution (![]() 8 Å) of the Lick standard
system (Worthey et al. 1994; Trager et al. 1998). The mean seeing during the
observing campaign varied between 0.8
8 Å) of the Lick standard
system (Worthey et al. 1994; Trager et al. 1998). The mean seeing during the
observing campaign varied between 0.8
![]() and 1.6
and 1.6
![]() ,
resulting in seeing-limited spectra. Consequently, the stellar disks
are smeared over 1-2 pixel along the spatial axis.
,
resulting in seeing-limited spectra. Consequently, the stellar disks
are smeared over 1-2 pixel along the spatial axis.
To ensure a representative sampling of the underlying stellar
population we obtained several spectra with slightly offset pointings.
In general three long-slit spectra were taken for each of our target
clusters (see Table 2 for details). The observing
pattern was optimized in time (i.e. in airmass) to obtain one spectrum
of the nuclear region and spectra of adjacent fields by shifting the
telescope a few arc seconds (i.e. ![]() 2 slit widths) to the North
and South. Exposure times were adjusted according to the surface
brightness of each globular cluster to reach an statistically secure
luminosity sampling of the underlying stellar population. Before and
after each block of science exposures, lamp spectra were taken for
accurate wavelength calibration.
2 slit widths) to the North
and South. Exposure times were adjusted according to the surface
brightness of each globular cluster to reach an statistically secure
luminosity sampling of the underlying stellar population. Before and
after each block of science exposures, lamp spectra were taken for
accurate wavelength calibration.
In addition to the globular cluster data, we obtained long-slit spectra of three stellar fields near the Galactic center (see Fig. 1). Two of them are located in Baade's Window. The exposure time for a single bulge spectrum is 1800 s. Five slightly offset pointings have been observed in each field resulting in 15 exposures of 30 min each.
During each night Lick and flux standard stars were observed for later index and flux calibrations. Table 2 shows the observing log of all three nights. Figure 1 gives the positions of all observed globular clusters (filled dots) and bulge fields (open squares) in the galactic coordinate system.
![\begin{figure}
\includegraphics[width=16.1cm,clip]{2781f1.eps} \end{figure}](/articles/aa/full/2002/43/aa2781/Timg67.gif) |
Figure 1: Distribution of galactic globular clusters as seen in the galactic coordinate system. The filled circles are the observed sample globular clusters while open circles mark the position of other known Milky Way globular clusters. All observed globular clusters are appropriately labeled. The positions were taken from the Globular Cluster Catalog by Harris (1996). Large squares show the positions of our three bulge fields for which spectroscopy is also available. Note that two of the three fields almost overlap in the plot. |
| Night | Targets | Exptime | RA(J2000) | Dec (J2000) | l[ |
b[ |
| 5.7.1999 | NGC 5927 | 3 |
15h 28m 00.5 s |
|
326.60 | 4.86 |
| NGC 6388 | 3 |
17h 36m 17.0 s |
|
345.56 | -6.74 | |
| NGC 6528 | 3 |
18h 04m 49.6 s |
|
1.14 | -4.17 | |
| NGC 6624 | 3 |
18h 23m 40.5 s |
|
2.79 | -7.91 | |
| NGC 6981 | 1 |
20h 53m 27.9 s |
|
35.16 | -32.68 | |
| Bulge1 | 5 |
18h 03m 12.1 s |
|
1.13 | 3.78 | |
| 6.7.1999 | NGC 6218 | 3 |
16h 47m 14.5 s |
|
15.72 | 26.31 |
| NGC 6441 | 3 |
17h 50m 12.9 s |
|
353.53 | -5.01 | |
| NGC 6553 | 3 |
18h 09m 15.6 s |
|
5.25 | -3.02 | |
| NGC 6626 | 3 |
18h 24m 32.9 s |
|
7.80 | -5.58 | |
| NGC 6981 | 1 |
20h 53m 27.9 s |
|
35.16 | -32.68 | |
| Bulge2 | 5 |
18h 05m 21.3 s |
|
1.26 | 4.23 | |
| 7.7.1999 | NGC 6284 | 3 |
17h 04m 28.8 s |
|
358.35 | 9.94 |
| NGC 5927 | 2 |
15h 28m 00.5 s |
|
326.60 | 4.86 | |
| NGC 6356 | 3 |
17h 23m 35.0 s |
|
6.72 | 10.22 | |
| NGC 6637 | 3 |
18h 31m 23.2 s |
|
1.72 | -10.27 | |
| NGC 6981 | 1 |
20h 53m 27.9 s |
|
35.16 | -32.68 | |
| Bulge3 | 5 |
17h 58m 38.3 s |
|
1.63 | 2.35 |
He-Ne-Ar-Fe lines were used to calibrate all spectra to better than
0.13 Å (rms). Unfortunately, the beam of the calibration lamp
covers only the central 3.3![]() along the slit's spatial axis
(perpendicular to the dispersion direction), which allows no precise
wavelength calibration for the outer parts close to the edge of the
CCD chip. We tried, however, to extrapolate a 2-dim.
along the slit's spatial axis
(perpendicular to the dispersion direction), which allows no precise
wavelength calibration for the outer parts close to the edge of the
CCD chip. We tried, however, to extrapolate a 2-dim.
![]() -calibration to the edges of the long-slit and found a
significant increase in the rms up to an unacceptable
0.7 Å. Hence, to avoid calibration biases we use data only from
regions which are covered by the arc lamp beam. Our effective slit
length is therefore 3.3
-calibration to the edges of the long-slit and found a
significant increase in the rms up to an unacceptable
0.7 Å. Hence, to avoid calibration biases we use data only from
regions which are covered by the arc lamp beam. Our effective slit
length is therefore 3.3![]() with a slit width of 3
with a slit width of 3
![]() .
For
each single pixel row along the dispersion axis an individual
wavelength solution was found and subsequently applied to each object,
bulge, and sky spectrum. After wavelength calibration the signal
along the spatial axis was averaged in
.
For
each single pixel row along the dispersion axis an individual
wavelength solution was found and subsequently applied to each object,
bulge, and sky spectrum. After wavelength calibration the signal
along the spatial axis was averaged in ![]() -space, i.e. the flux
of 3.3
-space, i.e. the flux
of 3.3![]() was averaged to obtain the final spectrum of a single
pointing.
was averaged to obtain the final spectrum of a single
pointing.
Finally, spectrophotometric standard stars, Feige 56, Feige 110, and Kopff 27 (Stone & Baldwin 1983; Baldwin & Stone 1984) were used to convert counts into flux units.
Following the rule of thumb, by which 1/10 of the instrumental
resolution (![]() 6.7 Å) transforms into the radial velocity
resolution, we estimate for our spectra a resolution of
6.7 Å) transforms into the radial velocity
resolution, we estimate for our spectra a resolution of
![]() 40 km s-1. In order to estimate the real uncertainty
we compare the radial velocity measurements of one globular cluster
(NGC 6981) which was observed in all three nights. We find a
dispersion in radial velocity
40 km s-1. In order to estimate the real uncertainty
we compare the radial velocity measurements of one globular cluster
(NGC 6981) which was observed in all three nights. We find a
dispersion in radial velocity
![]() km s-1 and a
maximal deviation of 32.4 km s-1. A comparison of measured radial
velocities of all our Lick standard stars with values taken from the
literature gives a dispersion of
km s-1 and a
maximal deviation of 32.4 km s-1. A comparison of measured radial
velocities of all our Lick standard stars with values taken from the
literature gives a dispersion of
![]() km s-1 which
matches the earlier rough estimate. In the case of NGC 6981, the internal error estimate (
km s-1 which
matches the earlier rough estimate. In the case of NGC 6981, the internal error estimate (
![]() km s-1) underestimates the real radial velocity uncertainty
assumed to be of the order of
km s-1) underestimates the real radial velocity uncertainty
assumed to be of the order of ![]() 40 km s-1 by a factor of
40 km s-1 by a factor of
![]() 2. Note however, that data of lower S/N will produce larger
radial velocity uncertainties. Moreover, taking into account the slit
width of 3
2. Note however, that data of lower S/N will produce larger
radial velocity uncertainties. Moreover, taking into account the slit
width of 3
![]() the maximum possible radial velocity error for a
star positioned at the edge of the slit is
the maximum possible radial velocity error for a
star positioned at the edge of the slit is ![]() 200 km s-1. For
high surface-brightness fluctuations inside the slit, this would
inevitably result in larger radial velocity errors than originally
expected from the calibration quality. Since we sum up all the flux
along the slit, we most effectively eliminate this surface-brightness
fluctuation effect. In fact, after a check of all our single spectra,
we find no exceptionally bright star inside the slit aperture, which
could produce a systematic deviation from the mean radial velocity.
200 km s-1. For
high surface-brightness fluctuations inside the slit, this would
inevitably result in larger radial velocity errors than originally
expected from the calibration quality. Since we sum up all the flux
along the slit, we most effectively eliminate this surface-brightness
fluctuation effect. In fact, after a check of all our single spectra,
we find no exceptionally bright star inside the slit aperture, which
could produce a systematic deviation from the mean radial velocity.
After all, we estimate that our real radial velocity
uncertainties are larger by a factor ![]() 2-4 than the values given
in Table 1.
2-4 than the values given
in Table 1.
The Lick system provides two sets of index passband definitions. One set of 21 passband definitions was published in Worthey et al. (1994) to which we will refer as the old set. A new and refined set of passband definitions is given in Trager et al. (1998) which is supplemented by the Balmer index definitions of Worthey & Ottaviani (1997). This new set of 25 indices is used throughout the subsequent analysis. However, we also provide Lick indices based on the old passband definitions (see Appendix D) which enable a consistent comparison with predictions from SSP models which make use of fitting functions based on the old set of passband definitions. Note that indices and model predictions which use two different passband definition sets are prone to systematic offsets. This point will be discussed in the second paper of the series (Maraston et al. 2002).
Before measuring indices, one has carefully to degrade spectra with
higher resolution to adapt to the resolution of the Lick system. We
strictly followed the approach of Worthey & Ottaviani (1997) and degraded our
spectra to the wavelength-dependent Lick resolution (![]() 11.5 Å at 4000 Å, 8.4 Å at 4900 Å, and 9.8 Å at 6000 Å). The
effective resolution (FWHM) of our spectra has been determined from
calibration-lamp lines and isolated absorption features in the object
spectra. The smoothing of our data is done with a wavelength-dependent
Gaussian kernel with the width
11.5 Å at 4000 Å, 8.4 Å at 4900 Å, and 9.8 Å at 6000 Å). The
effective resolution (FWHM) of our spectra has been determined from
calibration-lamp lines and isolated absorption features in the object
spectra. The smoothing of our data is done with a wavelength-dependent
Gaussian kernel with the width
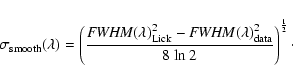 |
(1) |
The smoothing kernel for the bulge stellar fields is generally
narrower since one has to account for the non-negligible velocity
dispersion of bulge field stars. A typical line-of-sight velocity
dispersion
![]() km s-1 was assumed for
the bulge data (e.g. Spaenhauer et al. 1992). We do not correct for the
mean velocity dispersion of the globular clusters (
km s-1 was assumed for
the bulge data (e.g. Spaenhauer et al. 1992). We do not correct for the
mean velocity dispersion of the globular clusters (
![]() km s-1 Pryor & Meylan 1993).
km s-1 Pryor & Meylan 1993).
Another point of concern for low-S/N spectra (
![]() per
resolution element) is the slope of the underlying continuum
(see Beasley et al. 2000, for detailed discussion of this effect) which
influences the pseudo-continuum estimate for broad features and biases
the index measurement. However, since all our spectra are of high S/N(
per
resolution element) is the slope of the underlying continuum
(see Beasley et al. 2000, for detailed discussion of this effect) which
influences the pseudo-continuum estimate for broad features and biases
the index measurement. However, since all our spectra are of high S/N(![]() 50 per resolution element), we are not affected by a noisy
continuum.
50 per resolution element), we are not affected by a noisy
continuum.
After taking care of the resolution corrections, one has to correct
for systematic, higher-order effects. These variations are mainly due
to imperfect smoothing and calibration of the spectra. To correct the
small deviations 12 index standard stars from the list of
Worthey et al. (1994) have been observed throughout the observing run.
Figure 2 shows the comparison between the Lick data and
our index measurements for all passbands. Least-square fits using a
![]() -
-![]() -clipping (dashed lines) are used to parameterize the
deviations from the Lick system as a function of wavelength. The
functional form of the fit is
-clipping (dashed lines) are used to parameterize the
deviations from the Lick system as a function of wavelength. The
functional form of the fit is
| index | rms | units | ||
| CN1 | -0.0017 | -0.0167 | 0.0251 | mag |
| CN2 | -0.0040 | -0.0389 | 0.0248 | mag |
| Ca 4227 | -0.2505 | -0.0105 | 0.2582 | Å |
| G4300 | 0.6695 | -0.1184 | 0.4380 | Å |
| Fe 4384 | -0.5773 | 0.0680 | 0.2933 | Å |
| Ca 4455 | -0.1648 | 0.0249 | 0.4323 | Å |
| Fe 4531 | -0.3499 | 0.0223 | 0.1566 | Å |
| Fe 4668 | -0.8643 | 0.0665 | 0.5917 | Å |
| H |
0.0259 | 0.0018 | 0.1276 | Å |
| Fe 5015 | 1.3494 | -0.2799 | 0.3608 | Å |
| Mg1 | 0.0176 | -0.0165 | 0.0160 | mag |
| Mg2 | 0.0106 | 0.0444 | 0.0112 | mag |
| Mgb | 0.0398 | -0.0392 | 0.1789 | Å |
| Fe 5270 | -0.3608 | 0.0514 | 0.1735 | Å |
| Fe 5335 | -0.0446 | -0.0725 | 0.3067 | Å |
| Fe 5406 | -0.0539 | -0.0730 | 0.2054 | Å |
| Fe 5709 | -0.5416 | 0.3493 | 0.1204 | Å |
| Fe 5782 | -0.0610 | -0.0116 | 0.2853 | Å |
| NaD | 0.3620 | -0.0733 | 0.2304 | Å |
| TiO1 | 0.0102 | 0.2723 | 0.0133 | mag |
| TiO2 | -0.0219 | 0.1747 | 0.0342 | mag |
| H
|
-0.1525 | -0.0465 | 1.5633 | Å |
| H
|
0.4961 | 0.0117 | 0.6288 | Å |
| H
|
-0.1127 | -0.0639 | 0.4402 | Å |
| H
|
-0.0062 | -0.0343 | 0.1480 | Å |
Note, that most passbands require only a small linear offset, but no
offset as a function of index strength. While the former is simply due
to a small variation in the wavelength calibration, the latter is
produced by over/under-smoothing of the spectra. Absorption lines for
which the smoothing pushes the wings outside narrowly defined feature
passbands are mostly affected by this non-linear effect. However, for
passbands of major interest (such as CN, H![]() ,
Fe 5270, Fe 5335,
Mgb, and Mg2) the Lick indices are satisfactorily reproduced by a
simple offset (no tilt) in the index value (see
Fig. 2).
,
Fe 5270, Fe 5335,
Mgb, and Mg2) the Lick indices are satisfactorily reproduced by a
simple offset (no tilt) in the index value (see
Fig. 2).
Copyright ESO 2002