4 Line depth ratio and temperature variation of the active stars

Line-depth ratios variations are analysed separately for each active star considered. Since we have 10 different pairs of lines we have first analysed each ratio as a function of the rotational phase for the three stars and then we have transformed the LDRs in temperature. Some line pairs could not be used for our active star due to the non-negligible $v\sin i$ of the targets that causes blending of the lines that are too close in wavelength. Temperature values from all pairs for each spectrum were finally combined to yield an average temperature value, thus reducing the temperature errors. We have excluded from the means those LDR values that are outside the 3$\sigma$ box around the mean value.

Temperature variation curves have been obtained for each active star by folding in phase individual $<T_{\rm eff}>$ data, analogously to what is performed with photometric measurements.

As can be seen from Tables 5-7, our $<T_{\rm eff}>$ measurements span a time range of 4-5 stellar rotations, but it has been shown that the big spots observed in very active stars have typical lifetimes of several rotations. For a set of four spotted RS CVn stars, Henry et al. (1995) observed individual spot lifetimes between 0.5 years and over 6 years. Spot lifetimes in the same range were also found for other RS CVn stars, including VY Ari, IM Peg and HK Lac (Strassmeier & Bopp 1992; Strassmeier et al. 1994; Oláh et al. 1997; Strassmeier et al. 1997; Frasca et al. 1998).

4.1 VY Ari

Due to blends induced by the rotational broadening and by the crowding related to the spectral type of the visible component of VY Ari (K3-4 V-IV) only seven combinations of LDRs could be used for the temperature variation study. The useful measured line-depth ratios of VY Ari are plotted in Fig. 8 as a function of the rotational phase, computed from the following ephemeris

$${\rm HJD}_{\phi=0} = 24~~ 51856.0+16\hbox{$.\!\!^{\rm d}$ }1996~\times~E,$$ (5)

where the rotational period is taken from Strassmeier et al. (1997) and the epoch of zero phase corresponds to the first observing date (November 7th, 2000) at noon.

   

Table 5: Average surface temperature of VY Ari.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
856.4761	0.029	4799$~\pm~$16
857.4544	0.090	4767$~\pm~$9
859.4971	0.216	4760$~\pm~$13
860.4516	0.275	4798$~\pm~$5
861.4502	0.336	4822$~\pm~$6
862.4862	0.400	4821$~\pm~$13
863.5280	0.465	4850$~\pm~$4
864.5596	0.528	4895$~\pm~$4
865.4910	0.586	4916$~\pm~$21
866.5074	0.649	4899$~\pm~$7
867.5400	0.712	4850$~\pm~$12
913.3357	0.539	4855$~\pm~$8
915.3436	0.663	4909$~\pm~$2
916.3325	0.724	4888$~\pm~$9
917.4153	0.791	4881$~\pm~$4

Figure 8: LDRs of VY Ari versus rotational phase as computed according to Eq. (5). The temperature scale for each ratio is displayed on the right side of the boxes.

All LDRs show a clear modulation with the rotational phase with a maximum around $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }2$ and a minimum around $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }6$. The latter value, for all the LDRs, corresponds to the maximum temperature value as displayed on the right side scale. The amplitude variation of the LDRs ranges from 16% for the $\lambda$6252 V I-$\lambda$6253 Fe I ratio to 46% for the $\lambda$6266 V I-$\lambda$6265 Fe I ratio which appears to be the more sensitive to the temperature. These variations are well above (3-5 times) the average errors, which are determined according to error propagation rule as:

 

$$\frac{\sigma_r}{r} = \sqrt{\left( \frac{\sigma_{d_1}}{d_1} \right)^2 + \left( \frac{\sigma_{d_2}}{d_2} \right)^2},$$ (6)

where d₁ and d₂ are the line depths and $\sigma_{d_1}$ and $\sigma_{d_2}$ are the corresponding absolute errors as fixed by the S/Nratio for the measured continuum and central line flux.

Figure 9: Temperature curves of VY Ari obtained from the LDRs in Fig. 8 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.

Temperature values derived from the LDR- $T_{\rm eff}$ calibration from each pair are plotted in Fig. 9 using different symbols.

The temperature variation derived from all the LDRs displays a common behaviour, with a spread consistent with error estimate. Apart from the very similar shape, the temperature curves derived from different LDRs display a small offset one with respect to the other. Since we are mainly interested in the temperature variation, not in its absolute value, we have evaluated the average $T_{\rm eff}$ from all curves and have shifted each $T_{\rm eff}$ curve of the offset needed to make its average level equal to the average from all curves. These temperature offsets are in the range 20-50 K and may be due to some residual gravity dependence that has not been completely accounted for by the correction procedure or to the influence of some other physical parameter that has a minor effect on the LDR. This scaling procedure, applied to several LDRs, can statistically compensate for such effects and, also in the present case with only 6 or 7 useful LDRs, will give also a good evaluation of the absolute temperature scale that, however, has its intrinsic setting uncertainty of a few tens of Kelvin degrees (see e.g. Gray 1992).

We have then derived an average temperature variation by making a weighted mean of the values obtained from each spectrum. The weighted mean has been given by:

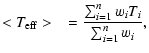$$<T_{\rm eff}>~~= \frac{\sum_{i=1}^{n} w_{i}T_{i}}{\sum_{i=1}^{n} w_i},$$ (7)

and the corresponding error has been computed as:

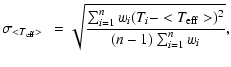$$\sigma_{<T_{\rm eff}>}~~ = \sqrt{\frac{\sum_{i=1}^{n} w_i(T_i - <T_{\rm eff}>)^2}{(n - 1)\sum_{i=1}^{n} w_i}},$$ (8)

where T_i = T(r_i) is the effective temperature obtained from the ith line-depth ratio, and $w_i = 1/\sigma_{T_i}^2$ is the corresponding statistical weight.

The final temperature variation ranges from 4739 K to 4916 K, i.e. with a $\Delta <T_{\rm eff}>$ = 177 K. As can be seen in Table 5, $\sigma_{<T_{\rm eff}>}$ errors are typically of a few Kelvin degree.

4.2 IM Peg

Figure 10: LDRs of IM Peg versus rotational phase as computed according to Eq. (9). The temperature scale for each ratio is displayed on the right side of the boxes.

For IM Peg we were also able to use seven LDRs, but with some differences, as displayed in Fig. 10, where single LDR values are plotted as function of the rotational phase. Phases are reckoned from the ephemeris given by Strassmeier et al. (1997)

$${\rm HJD}_{\phi=0} = 24~~ 43734.0+24\hbox{$.\!\!^{\rm d}$ }494~\times~E.$$ (9)

In this case the amplitude of the LDR variation is smaller and the average behaviour is more noisy and not well defined.

IM Peg actually represents a proper test case for the application and reliability of the method. Its rotational broadening (26.5 km s^-1) is a bit larger than our spectral resolution so that the Doppler shifts of the bumps produced by the spots could be partially resolved in our spectra, and for sure are responsible for the larger noise. As a matter of fact, Berdyugina et al. (2000) from high resolution spectra (R = 30 000-80 000) were able to obtain surface images with the Doppler-imaging technique.

Notwithstanding this limitation a maximum LDR variation of 37% is obtained for the $\lambda$6275 V I-$\lambda$6270 Fe I ratio.

   

Table 6: Average surface temperature of IM Peg.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
798.4555	0.242	4615$~\pm~$8
800.4203	0.322	4608$~\pm~$4
801.4724	0.365	4666$~\pm~$7
829.4298	0.507	4654$~\pm~$18
830.3874	0.546	4645$~\pm~$19
831.3436	0.585	4622$~\pm~$13
833.3725	0.668	4589$~\pm~$6
835.3963	0.750	4569$~\pm~$9
856.3316	0.605	4621$~\pm~$11
859.3944	0.730	4585$~\pm~$10
860.2836	0.766	4606$~\pm~$9
861.2989	0.808	4593$~\pm~$5
862.3525	0.851	4578$~\pm~$25
863.3614	0.892	4547$~\pm~$6
865.3533	0.973	4613$~\pm~$14
913.2565	0.929	4582$~\pm~$14
915.2733	0.011	4574$~\pm~$7
917.3364	0.096	4585$~\pm~$12

However, all the LDRs converted to temperature and combined in a single temperature curve, as displayed in Fig. 11, lead to a fairly well-defined temperature variation as a function of the rotational phase. The average curve obtained from the weighted mean (lower panel in Fig. 11) appears still well defined. The temperature maximum, with a value of 4666 K, occurs around phase $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }5$. The full amplitude variation is $\Delta <T_{\rm eff}>$ = 119 K, corresponding to a 3% of the determined average temperature value.

Figure 11: Temperature curves of IM Peg obtained from the LDRs in Fig. 10 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.

4.3 HK Lac

Figure 12: LDRs of HK Lac versus rotational phase as computed according to Eq. (10). The temperature scale for each ratio is displayed on the right side of the boxes.

For HK Lac we were able to use six LDRs, as displayed in Fig. 12 where single values are plotted as a function of the rotational phase computed from the ephemeris

$${\rm HJD}_{\phi=0} = 24~~ 40017.17+24\hbox{$.\!\!^{\rm d}$ }4284~\times~E,$$ (10)

which is the orbital ephemeris already given by Gorza & Heard (1971) with the initial epoch given by Strassmeier et al. (1993) corresponding to inferior conjunction (more massive star closer to the observer).

All the ratios exhibit a well-defined parallel behaviour; even single values have slightly larger errors due to the average lower S/N ratio of the observations.

   

Table 7: Average surface temperature of HK Lac.

HJD	$\phi$	$~~<T_{\rm eff}>$
(+2 451 000)		(K)
798.4325	0.277	4686$~\pm~$3
800.4422	0.360	4716$~\pm~$15
801.4907	0.402	4698$~\pm~$52
830.3564	0.584	4765$~\pm~$8
831.3613	0.625	4720$~\pm~$12
833.3913	0.708	4734$~\pm~$12
835.4153	0.791	4709$~\pm~$3
836.4205	0.832	4689$~\pm~$12
856.3085	0.646	4741$~\pm~$33
858.2968	0.728	4708$~\pm~$15
860.2632	0.808	4724$~\pm~$19
861.2775	0.850	4702$~\pm~$17
862.3297	0.893	4660$~\pm~$6
863.3362	0.934	4682$~\pm~$8
865.3329	0.016	4640$~\pm~$14
913.2360	0.977	4651$~\pm~$11
915.2508	0.059	4656$~\pm~$2
916.2584	0.101	4641$~\pm~$7
917.3159	0.144	4638$~\pm~$31

The largest amplitude variation is displayed by the V I-Fe II at 6243 Å and 6247 Å, with a full variation of 40%. The corresponding temperature range is very similar for all the LDRs, as displayed in Fig. 13 (upper panel) where the temperature values deduced according to the above calibrations are plotted. The spread of the points is consistent with the estimated errors, and the mean curve resulting from weighted average has a well defined variation. The temperature maximum of 4765 K seems to occur around phase $0~\hbox{$.\!\!^{\scriptscriptstyle\rm p}$ }6$. The temperature variation we get is 127 K, corresponding to $\simeq$3% of the average value.

Figure 13: Temperature curves of HK Lac obtained from the LDRs in Fig. 12 (upper panel). Different symbols have been used for the different ratios. The average effective temperature $<T_{\rm eff}>$ as a function of rotational phase is displayed in the lower panel.