Various methods have been used to remove background flares from XMM-Newton and
Chandra data sets. For XMM-Newton observations, perhaps the most
simple is direct visual inspection of the binned high-energy (10-12)
keV light curve over the whole field of view, the adoption of a
threshold level, and the exclusion of any intervals above the selected
threshold (see e.g., Arnaud et al. 2001). For Chandra data,
an ![]() clipping is used, where the average count rate in the (3-6) keV band over the field of view is calculated, thresholds are set
depending on this value, and the light curve cleaned for any intervals
where the thresholds are not met.
clipping is used, where the average count rate in the (3-6) keV band over the field of view is calculated, thresholds are set
depending on this value, and the light curve cleaned for any intervals
where the thresholds are not met.
It is known that the XMM-Newton quiescent background level is variable by
![]()
![]() ,
and so it is not possible to set a rigid threshold
level for flare rejection because of the risk of losing good data.
The threshold level should ideally be dependent on the quiescent rate
of the observation in question.
,
and so it is not possible to set a rigid threshold
level for flare rejection because of the risk of losing good data.
The threshold level should ideally be dependent on the quiescent rate
of the observation in question.
For the A1413 observation, we extracted the MOS (10-12) keV light
curves in the field of view in 104 s bins (chosen as this is an
integral multiple of the frame readout time). Similar light curves
were made for the pn, but in the (12-14) keV band. We then made a
histogram of each light curve and fitted this histogram with a
Poisson distribution
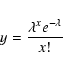 |
(A.1) |
This method is effective at finding the quiescent periods,
even for data strongly affected by flares. As such it is not prone to
the overestimation of the mean rate, the main problem with the
![]() clipping method.
clipping method.
Copyright ESO 2002