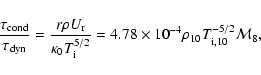Up: Ion-dominated plasma and the
Angular momentum in standard disks (Shakura & Sunyaev 1973, hereforth SS-disks)
is transported outwards mainly via small scale magneto-hydrodynamical
turbulence. Magnetic fields (-MFs) however were assumed to be weak, and remain so during
the whole viscous evolution of the disk.
Here we adopt a different view. Let
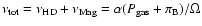 be a modified dynamical viscosity (see
the caption of Fig. 1 for elaboration).
Unlike
be a modified dynamical viscosity (see
the caption of Fig. 1 for elaboration).
Unlike
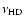 which transports angular momentum outwards,
which transports angular momentum outwards,
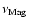 transports angular momentum in the vertical direction, provided that
transports angular momentum in the vertical direction, provided that 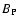 is of large scale topology. Taking into account that
is of large scale topology. Taking into account that
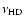 in SS-disks
decreases inwards, a transition radius
in SS-disks
decreases inwards, a transition radius
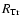 at which
result
at which
result![[*]](/icons/foot_motif.gif) .
the time scale of angular momentum removal
by MFs at
.
the time scale of angular momentum removal
by MFs at
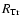 is of the same order as that by the turbulent viscosity. Hence
is of the same order as that by the turbulent viscosity. Hence
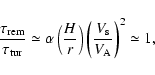 |
(1) |
where
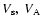 are the sound and transverse
are the sound and transverse
 speeds
speeds
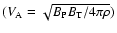 ,
respectively.
Taking into account that
,
respectively.
Taking into account that
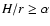 ,
we end up with
,
we end up with
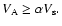 The last optimistic inequality applies everywhere in the disk, irrespective whether
turbulence is mediated by
The last optimistic inequality applies everywhere in the disk, irrespective whether
turbulence is mediated by
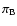 or not. Therefore, vertical transport of angular momentum via MFs
is at least as efficient as
or not. Therefore, vertical transport of angular momentum via MFs
is at least as efficient as 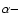 viscosity. This is even more justified by the fact that
Balbus-Hawley instability in Keplerian-disks
amplifies initially weak fields to considerably large values,
but remain still below equipartition (Hawley et al. 1996). Imposing appropriate
boundary conditions, and carrying the MHD-Box calculations with high spatial
resolution, MFs could be amplified up to equipartition (Ziegler 2002), yielding thereby
viscosity. This is even more justified by the fact that
Balbus-Hawley instability in Keplerian-disks
amplifies initially weak fields to considerably large values,
but remain still below equipartition (Hawley et al. 1996). Imposing appropriate
boundary conditions, and carrying the MHD-Box calculations with high spatial
resolution, MFs could be amplified up to equipartition (Ziegler 2002), yielding thereby
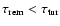 .
Furthermore, the dynamo-action model proposed by Tout & Pringle (1992), if applied, would make
.
Furthermore, the dynamo-action model proposed by Tout & Pringle (1992), if applied, would make
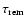 even shorter.
even shorter.
To be noted here that when taking a more realistic density and temperature stratification
in global 3D MHD disk-calculations, vertical transport of angular momentum is inevitable (Arlt 2002).
Efficient vertical transport of angular momentum rises the following important issues:
1) Turbulence in the disk need not be dissipated, or it might be even suppressed by the
amplified  .
This allows accretion to evolve without necessarily
emitting the bulk of the their potential energy as radiation, and gives rise to
energy re-distribution.
2) Accretion flows may not proceed as slowly as in
SS-disk, but they may turn into
advection-dominated
.
This allows accretion to evolve without necessarily
emitting the bulk of the their potential energy as radiation, and gives rise to
energy re-distribution.
2) Accretion flows may not proceed as slowly as in
SS-disk, but they may turn into
advection-dominated![[*]](/icons/foot_motif.gif) .
This occurs because
the time scale of angular momentum removal
from the disk scales as:
.
This occurs because
the time scale of angular momentum removal
from the disk scales as:
 |
(2) |
where
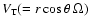 is the angular velocity (Fig. 1).
This indicates that angular momentum removal is more efficient at smaller radii.
is the angular velocity (Fig. 1).
This indicates that angular momentum removal is more efficient at smaller radii.
To maintain dynamical stability, angular
momentum removal from the disk should be compensated by rapid advection from larger radii,
i.e.,
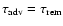 .
Further, rapid and steady generation of
.
Further, rapid and steady generation of 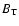 in the disk yields
in the disk yields
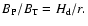 The later two conditions imply that the radial velocity
The later two conditions imply that the radial velocity
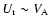 ,
which means that the stronger the MF threading the disk, the more advection-dominated
it becomes, and therefore the faster is the establishment of the super-Keplerian layer.
,
which means that the stronger the MF threading the disk, the more advection-dominated
it becomes, and therefore the faster is the establishment of the super-Keplerian layer.
Based on the present calculations
(see the caption of Figs. 1 and 2-5), it is found that: 1) Angular velocity
in the transition layer (TL) adopts approximately the profile
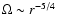 .
2) Energy dissipation is injected primarily
into the ions that cool predominantly through fast outflows.
3) The generated
toroidal magnetic field is quenched by a magnetic diffusion (reconnection)
and fast outflows.
The width of the TL is pre-dominantly determined through the transverse
variation of the ion-pressure across the jet, i.e.,
.
2) Energy dissipation is injected primarily
into the ions that cool predominantly through fast outflows.
3) The generated
toroidal magnetic field is quenched by a magnetic diffusion (reconnection)
and fast outflows.
The width of the TL is pre-dominantly determined through the transverse
variation of the ion-pressure across the jet, i.e.,
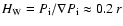 ,
and so strongly dependent on whether the flow is a one- or two-temperature plasma.
In the steady-state case, this implies:
,
and so strongly dependent on whether the flow is a one- or two-temperature plasma.
In the steady-state case, this implies:
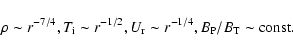 |
(3) |
We note that 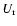 adopts a profile and attains values similar to those
in the innermost part of the disk.
Provided that energy exchange between the matter
in the disk and in the TL is efficient, the incoming matter can easily be
re-directed into outwards-oriented motions. This implies that the Bernoulli number (Be)
can change sign in dissipative flows. As Fig. 5 shows,
Be is everywhere negative save the TL, where it attains large positive
values, so that the ion-plasma can start its kpc-journey.
Worth-noting is the resulting MF topology (see Fig. 4). Apparently, the outflow
is sufficiently strong to shift the MF lines outwards, while the large
diffusivity prevents the formation of large electric currents along the equator. In the corona
however, MFs are too weak to halt the diffusive plasma in the dynamically unstable
corona against gravity, and instead, they drift with the
infalling gas inwards. In the case of very weak MFs (
adopts a profile and attains values similar to those
in the innermost part of the disk.
Provided that energy exchange between the matter
in the disk and in the TL is efficient, the incoming matter can easily be
re-directed into outwards-oriented motions. This implies that the Bernoulli number (Be)
can change sign in dissipative flows. As Fig. 5 shows,
Be is everywhere negative save the TL, where it attains large positive
values, so that the ion-plasma can start its kpc-journey.
Worth-noting is the resulting MF topology (see Fig. 4). Apparently, the outflow
is sufficiently strong to shift the MF lines outwards, while the large
diffusivity prevents the formation of large electric currents along the equator. In the corona
however, MFs are too weak to halt the diffusive plasma in the dynamically unstable
corona against gravity, and instead, they drift with the
infalling gas inwards. In the case of very weak MFs (
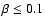 ),
our calculations indicate a considerably weak outflow. This is a consequence of the tendency of
the MFs to establish a monopole like-topology, i.e, a one-dimensional MF-topology in which
),
our calculations indicate a considerably weak outflow. This is a consequence of the tendency of
the MFs to establish a monopole like-topology, i.e, a one-dimensional MF-topology in which
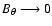 .
In this case, the magnetic tension
.
In this case, the magnetic tension
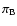 becomes inefficient in feeding the matter
in the TL with the angular momentum required for launching jets, indicating herewith that
cold accretion disks alone are in-appropriate for initiating winds (Ogilvie & Livio 2001).
becomes inefficient in feeding the matter
in the TL with the angular momentum required for launching jets, indicating herewith that
cold accretion disks alone are in-appropriate for initiating winds (Ogilvie & Livio 2001).
![\begin{figure}
\par\includegraphics[width=7cm,clip]{Eg221_f2.ps}
\end{figure}](/articles/aa/full/2002/40/aaeg221/Timg66.gif) |
Figure 2:
The horizontal distribution of the normalized density 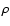 ,
angular velocity ,
angular velocity 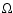 ,
radial and horizontal velocities ,
radial and horizontal velocities
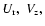 the radial and horizontal
MF-components
the radial and horizontal
MF-components
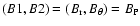 and the toroidal
MF-component
and the toroidal
MF-component 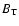 at r=2.5. Note the density plateau,
the positive radial velocity (outflows), the super-Keplerian rotation and
the strongly enhanced strength of the MF-components in the TL. The inwards-oriented
motions in the disk (inflows) and strongly increasing density towards the equator
are obvious.
at r=2.5. Note the density plateau,
the positive radial velocity (outflows), the super-Keplerian rotation and
the strongly enhanced strength of the MF-components in the TL. The inwards-oriented
motions in the disk (inflows) and strongly increasing density towards the equator
are obvious. |
Comparing the flux of matter in the wind to that in the disk, we find that
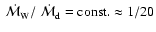 .
The angular momentum flux associated with
the wind is
.
The angular momentum flux associated with
the wind is
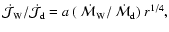 where a is a constant of order unity.
Consequently, at
where a is a constant of order unity.
Consequently, at
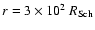 ,
almost
,
almost 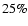 of the total accreted angular momentum
in the disk re-appears in the wind.
of the total accreted angular momentum
in the disk re-appears in the wind.
Why is the TL geometrically thin?
In stratified dissipative flows the density scale height is much smaller than
the scale height of the angular velocity (Hujeirat & Camenzind 2000). Since the flow
in TL rotates super-Keplerian, Coriolis forces act to compress the
disk-matter and make its density scale height even smaller. This implies that advective-disks
are geometrically thin, much thinner than what ADAF-solutions predict.
On the other hand, unless there is a significant energy flux that heats up the plasma
from below, as in the case of stars, heat conduction will always force the BH-coronae
to collapse dynamically.
To elaborate this point, let us compare the conduction time scale with the dynamical
time scale along 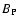 -field at the last stable orbit of a
SMBH:
-field at the last stable orbit of a
SMBH:
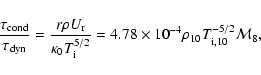 |
(4) |
where 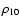 ,
,
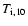 and
and
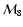 are respectively in
are respectively in
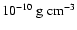 ,
1010 K and in
,
1010 K and in
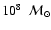 units.
This is much less than unity for most reasonable values of density and temperature typical for
AGN-environments. In writing Eq. (4) we have taken optimistically the upper limit
units.
This is much less than unity for most reasonable values of density and temperature typical for
AGN-environments. In writing Eq. (4) we have taken optimistically the upper limit
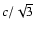 for the velocity,
and set
for the velocity,
and set
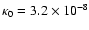 for the ion-conduction coefficient.
When modifying the conduction operator to respect causality, we obtain
for the ion-conduction coefficient.
When modifying the conduction operator to respect causality, we obtain
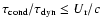 ,
which is again smaller than unity.
,
which is again smaller than unity.
This agrees with our numerical calculations which rule out the
possibility of outflows along the rotation axis, and in particular not
from the highly unstable polar region of the BH, as ADAF-solutions predict.
![\begin{figure}
\par\includegraphics*[width=16cm,clip]{Eg221_f3.ps}
\end{figure}](/articles/aa/full/2002/40/aaeg221/Timg80.gif) |
Figure 3:
The distribution of the velocity field superposed on the logarithmic-scaled ratio of the ion- to electron-temperatures (red color corresponds to high ratios
and blue to low-ratios). The lower figure is a zoom-in of the flow
configuration in the innermost part of the disk. |


Up: Ion-dominated plasma and the
Copyright ESO 2002
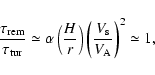
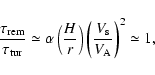
![]() .
This allows accretion to evolve without necessarily
emitting the bulk of the their potential energy as radiation, and gives rise to
energy re-distribution.
2) Accretion flows may not proceed as slowly as in
SS-disk, but they may turn into
advection-dominated
.
This allows accretion to evolve without necessarily
emitting the bulk of the their potential energy as radiation, and gives rise to
energy re-distribution.
2) Accretion flows may not proceed as slowly as in
SS-disk, but they may turn into
advection-dominated![]() .
This occurs because
the time scale of angular momentum removal
from the disk scales as:
.
This occurs because
the time scale of angular momentum removal
from the disk scales as:
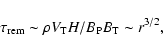
![]() .
Further, rapid and steady generation of
.
Further, rapid and steady generation of ![]() in the disk yields
in the disk yields
![]() The later two conditions imply that the radial velocity
The later two conditions imply that the radial velocity
![]() ,
which means that the stronger the MF threading the disk, the more advection-dominated
it becomes, and therefore the faster is the establishment of the super-Keplerian layer.
,
which means that the stronger the MF threading the disk, the more advection-dominated
it becomes, and therefore the faster is the establishment of the super-Keplerian layer.
![]() .
2) Energy dissipation is injected primarily
into the ions that cool predominantly through fast outflows.
3) The generated
toroidal magnetic field is quenched by a magnetic diffusion (reconnection)
and fast outflows.
The width of the TL is pre-dominantly determined through the transverse
variation of the ion-pressure across the jet, i.e.,
.
2) Energy dissipation is injected primarily
into the ions that cool predominantly through fast outflows.
3) The generated
toroidal magnetic field is quenched by a magnetic diffusion (reconnection)
and fast outflows.
The width of the TL is pre-dominantly determined through the transverse
variation of the ion-pressure across the jet, i.e.,
![]() ,
and so strongly dependent on whether the flow is a one- or two-temperature plasma.
In the steady-state case, this implies:
,
and so strongly dependent on whether the flow is a one- or two-temperature plasma.
In the steady-state case, this implies:
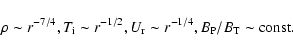
![]() .
The angular momentum flux associated with
the wind is
.
The angular momentum flux associated with
the wind is
![]() where a is a constant of order unity.
Consequently, at
where a is a constant of order unity.
Consequently, at
![]() ,
almost
,
almost ![]() of the total accreted angular momentum
in the disk re-appears in the wind.
of the total accreted angular momentum
in the disk re-appears in the wind. ![]() -field at the last stable orbit of a
SMBH:
-field at the last stable orbit of a
SMBH: