

Up: Ion-dominated plasma and the
1 Introduction
Jets have been observed in many systems including active galaxies, X-ray binaries,
black holes X-ray transients, supersoft X-ray sources and young stellar objects
(Königl 1997; Livio 1999; Mirabel 2001).
Each of these systems is considered to contain an accretion disk, while
jet-speeds have been verified to be of the order of the escape velocity at the
vicinity of the central object (Mirabel 1999; Livio 1999 and the references therein).
Recent observations of the M 87 galaxy reveal a significant jet-collimation
already at 100 gravitational radii from the central engine, and that jet-launching
should occur close to the last stable orbit (Biretta et al. 2002).
Several scenarios have been suggested to uncover the mechanisms underlying
jet-initiations and their connection to accretion disks (Pudritz & Norman 1986).
In most of these models magnetic
fields (-MFs) are considered to play
the major role in powering and collimating jets (e.g., the magneto-centrifugal acceleration
model of Blandford & Payne 1982, the ion-torus model of Rees et al. 1982, X-point
model of Shu et al. 1994, ADAF and ADIOS models of Narayan & Yi 1995 and
Blandford & Begelman 1999).
Previous radiative hydrodynamical studies without magnetic fields have confirmed
the formation of a transition
layer (-TL) between the disk and the corona, governed by thermally-induced
outflows (Hujeirat & Camenzind 2000).
The aim of this paper is to show that incorporating large scale magnetic fields (-MFs)
manifests such formation and dramatically strengthen the dynamic of the in- and
out-flows. Moreover, the TL is shown to be an optimal runaway region
where highly energetic ion-jets start off. The back reaction of jet-flows
on the structure of the disk and on the corona surrounding the nucleus is investigated also.
The study is based on self-consistent 3D axi-symmetric quasi-stationary MHD calculations,
taking into account magnetic and hydro-turbulent diffusion, and adopting the two-temperature
description (Shapiro et al. 1976).
This adaptation is fundamental as 1) the dynamical time scale
around the last stable orbit may become shorter than the Coulomb-coupling time. Therefore
turbulent dissipation, adiabatic or shock compression preferentially heat up the ions rather than
electrons (
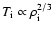 ,
while
,
while
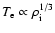 ).
2) Taking into account that ions radiate inefficiently, having virial-heated ions
in the vicinity of the last stable orbit
is essential for the total energy-budget of large scale jets.
).
2) Taking into account that ions radiate inefficiently, having virial-heated ions
in the vicinity of the last stable orbit
is essential for the total energy-budget of large scale jets.
![\begin{figure}
\par\includegraphics[width=8.0cm,clip]{Eg221_f1.eps}
\end{figure}](/articles/aa/full/2002/40/aaeg221/Timg38.gif) |
Figure 1:
The model consists of
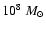 Schwarzschild BH at the center
(its gravity
is described in terms of the quasi-Newtonian potential of Paczynski & Wiita 1980),
and an SS-disk (blue color, extending from r=1 to r=20 in units of the radius of the
last stable orbit i.e., in
Schwarzschild BH at the center
(its gravity
is described in terms of the quasi-Newtonian potential of Paczynski & Wiita 1980),
and an SS-disk (blue color, extending from r=1 to r=20 in units of the radius of the
last stable orbit i.e., in
 ,
thickness ,
thickness
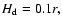 an accretion rate of
an accretion rate of
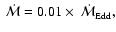 and a
central disk
temperature of
and a
central disk
temperature of
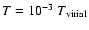 at the outer radius). The ion-temperature
at the outer radius). The ion-temperature
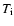 is set to be equal to the electron temperature
is set to be equal to the electron temperature
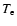 initially.)
The low-density hot corona
(
initially.)
The low-density hot corona
(
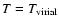 ,
and density ,
and density
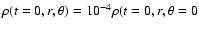 )
is set to envelope the disk.
A large scale magnetic field is set to thread the disk and the overlying corona
(blue lines, )
is set to envelope the disk.
A large scale magnetic field is set to thread the disk and the overlying corona
(blue lines,
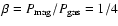 at the outer radius,
where
at the outer radius,
where
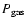 is the ion-pressure, is the ion-pressure,
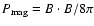 is the magnetic pressure, and B is the magnetic field whose components are
is the magnetic pressure, and B is the magnetic field whose components are
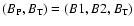 .)
The low-density hot corona
( .)
The low-density hot corona
(
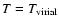 ,
and density ,
and density
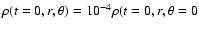 )
is set to envelope the disk.
A large scale magnetic field is set to thread the disk and the overlying corona
(blue lines, )
is set to envelope the disk.
A large scale magnetic field is set to thread the disk and the overlying corona
(blue lines,
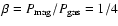 at the outer radius, where
at the outer radius, where
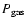 is the ion-pressure, is the ion-pressure,
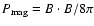 is the magnetic pressure, and B is the magnetic field whose components are
is the magnetic pressure, and B is the magnetic field whose components are
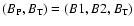 .)
The numerical procedure is based on using the implicit solver IRMHD3 to search steady-state
solution for the 3D axi-symmetric two-temperature diffusive MHD equations in spherical
geometry (for further clarifications about the equations and the numerical method
see Hujeirat & Rannacher 2001; Hujeirat & Camenzind 2000).
The ion-pressure is used to describe the turbulent viscosity: .)
The numerical procedure is based on using the implicit solver IRMHD3 to search steady-state
solution for the 3D axi-symmetric two-temperature diffusive MHD equations in spherical
geometry (for further clarifications about the equations and the numerical method
see Hujeirat & Rannacher 2001; Hujeirat & Camenzind 2000).
The ion-pressure is used to describe the turbulent viscosity:
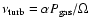 ,
where ,
where 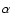 is the usual viscosity
coefficient, and
is the usual viscosity
coefficient, and 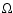 is
the angular frequency. The magnetic diffusivity
is taken to be equal to
is
the angular frequency. The magnetic diffusivity
is taken to be equal to
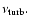
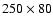 strongly stretched finite volume cells in the radial and vertical direction
have been used. Normal symmetry and anti-symmetry boundary conditions have been imposed along
the equator and the rotation axis. Extrapolation has been adopted to fix down-stream values
at the inner boundary. Non-dimensional formulation is adopted, using the reference scaling variables:
strongly stretched finite volume cells in the radial and vertical direction
have been used. Normal symmetry and anti-symmetry boundary conditions have been imposed along
the equator and the rotation axis. Extrapolation has been adopted to fix down-stream values
at the inner boundary. Non-dimensional formulation is adopted, using the reference scaling variables:
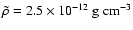 , ,
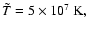
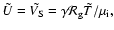
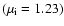 . .
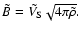 The location of the transition layer (-TL), where the ion-dominated plasma
is expected to rotate super-Keplerian and being accelerated into jets,
is shown for clarity.
The location of the transition layer (-TL), where the ion-dominated plasma
is expected to rotate super-Keplerian and being accelerated into jets,
is shown for clarity.
|


Up: Ion-dominated plasma and the
Copyright ESO 2002
![]() ,
while
,
while
![]() ).
2) Taking into account that ions radiate inefficiently, having virial-heated ions
in the vicinity of the last stable orbit
is essential for the total energy-budget of large scale jets.
).
2) Taking into account that ions radiate inefficiently, having virial-heated ions
in the vicinity of the last stable orbit
is essential for the total energy-budget of large scale jets.