3 Power spectrum of the 60 and 100
For a given image, the power spectrum P(k) is
the absolute value of the Fourier Transform (we use
the Fast Fourier Transform (FFT) function of IDL)
of the image, averaged over constant values of
![]() .
To make sure that map boundaries are not
contaminating the computed power spectrum, we apodize the image with a
cosine function before computing the Fourier Transform. This prevents
the introduction of strong discontinuities when the image is periodized
in the FFT algorithm (see Appendix A).
.
To make sure that map boundaries are not
contaminating the computed power spectrum, we apodize the image with a
cosine function before computing the Fourier Transform. This prevents
the introduction of strong discontinuities when the image is periodized
in the FFT algorithm (see Appendix A).
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{H3453F1.ps}
\end{figure}](/articles/aa/full/2002/39/aah3453/Timg21.gif) |
Figure 1:
Top left: the 100 |
The power spectrum of the 100 ![]() m ISSA map of one of our fields is shown in Fig. 1.
Since the zodiacal emission has been subtracted in the ISSA maps,
there are four main contributions to the power
spectrum at these wavelengths:
the cirrus emission, point sources,
the CIB (resolved and unresolved) and the noise.
Therefore, and if the noise and the signal are not correlated,
the power spectrum P(k)
can be expressed in the following manner:
m ISSA map of one of our fields is shown in Fig. 1.
Since the zodiacal emission has been subtracted in the ISSA maps,
there are four main contributions to the power
spectrum at these wavelengths:
the cirrus emission, point sources,
the CIB (resolved and unresolved) and the noise.
Therefore, and if the noise and the signal are not correlated,
the power spectrum P(k)
can be expressed in the following manner:
One of the main limitation of the component separation to the power spectrum is the estimate of the noise contribution. For ISSA maps, this contribution can be estimated accurately as they are the combination of up to three HCON maps. Indeed the noise power spectrum of the HCON maps, and therefore of the ISSA map, can be estimated by subtracting two HCON maps of the same region. An example of the difference between two HCON maps for a typical low brightness ISSA map is shown in Fig. 1 (top-right). The characteristic stripping of the IRAS data is seen in this difference map. The distribution of difference values is symmetric (when there is no strong point sources) and well fitted by a sum of two Gaussian functions (see Fig. 1, bottom-right).
As the distribution of the difference values is the sum of two Gaussian functions with
an equivalent width
![]() and assuming that the noise in the IRAS survey
is stationary to a good approximation (as tested below), we can conclude that the noise
of an individual HCON can also be characterized by an equivalent width:
and assuming that the noise in the IRAS survey
is stationary to a good approximation (as tested below), we can conclude that the noise
of an individual HCON can also be characterized by an equivalent width:
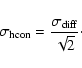 |
(2) |
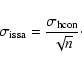 |
(3) |
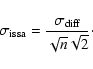 |
(4) |
In general three HCON maps were averaged but parts of them may be undefined.
Therefore, for each ISSA map we looked at the three corresponding HCON maps and
built a mask n(x,y) that gives the number of defined values that were averaged at each positions.
Then, the noise map of a given ISSA map is estimated by subtracting
two HCON maps and divide the result by
![]() .
.
The power spectra of the ISSA map and of its noise map are shown in Fig. 1 (bottom-left).
Both power spectra meet at small scales (
![]() pixel-1)
where the signal is noise dominated. The noise map is characterized by a
pixel-1)
where the signal is noise dominated. The noise map is characterized by a ![]() k-0.8 power spectrum.
We have investigated the variations of the statistical properties of the noise
on ISSA maps where three complete HCONs exists. By looking at the three possible
difference maps built from three HCONs, we found that
the shape of the power spectrum
of the noise is rather constant with time and that the absolute level of the noise varies
by less than 15% from one HCON to the other.
This is equally true at 60 and 100
k-0.8 power spectrum.
We have investigated the variations of the statistical properties of the noise
on ISSA maps where three complete HCONs exists. By looking at the three possible
difference maps built from three HCONs, we found that
the shape of the power spectrum
of the noise is rather constant with time and that the absolute level of the noise varies
by less than 15% from one HCON to the other.
This is equally true at 60 and 100 ![]() m.
m.
The multiplicative factor ![]() in Eq. (1) represents
the effective instrumental filter function of the system
(telescope, focal plane assembly, sky scanning and map making).
For some ISSA maps the instrumental function can be estimated directly from the power
spectrum of the map. This is the case for maps where the brightness fluctuations are dominated by the cirrus
emission and where the power spectrum is simply:
in Eq. (1) represents
the effective instrumental filter function of the system
(telescope, focal plane assembly, sky scanning and map making).
For some ISSA maps the instrumental function can be estimated directly from the power
spectrum of the map. This is the case for maps where the brightness fluctuations are dominated by the cirrus
emission and where the power spectrum is simply:
| (5) |
To estimate ![]() directly on the power spectrum of ISSA maps, we have selected 20 relatively bright
regions (mean brightness greater than 8 MJy/sr) where the noise and CIB contributions are negligible.
To make sure that the fluctuations are dominated by the cirrus emission, point sources were filtered
out using a median filtering. An example of the power spectrum of such
an ISSA map is shown in Fig. 2.
We found that the effective IRAS instrumental filter function in Fourier space is well describe
by a Gaussian function both at 60 and 100
directly on the power spectrum of ISSA maps, we have selected 20 relatively bright
regions (mean brightness greater than 8 MJy/sr) where the noise and CIB contributions are negligible.
To make sure that the fluctuations are dominated by the cirrus emission, point sources were filtered
out using a median filtering. An example of the power spectrum of such
an ISSA map is shown in Fig. 2.
We found that the effective IRAS instrumental filter function in Fourier space is well describe
by a Gaussian function both at 60 and 100 ![]() m.
To determine the width of the instrumental function,
the power spectrum of the 20 fields were fitted by the following equation:
m.
To determine the width of the instrumental function,
the power spectrum of the 20 fields were fitted by the following equation:
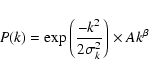 |
(6) |
The cutoff seen in Fig. 2 at frequencies larger than 0.05 arcmin-1
is where the effect of the instrumental filter function is expected.
When the power spectrum is divided by the Gaussian instrumental function (grey line)
one sees that this modeling does not stand
for scales smaller than 4.5 arcmin (k > 0.22 arcmin-1).
This is due to the effective resolution of the IRAS data.
The power spectrum has to be cut at the Nyquist frequency
corresponding to the 1.5' pixel ISSA map.
However, the effective resolution of the IRAS data is
about 3.8' and 4.25' respectively at 60 and 100 ![]() m. For that reason,
all the power spectrum at frequency above 0.1 arcmin-1, which corresponds
to the Nyquist frequency of the effective resolution, has to be taken
with cautious.
m. For that reason,
all the power spectrum at frequency above 0.1 arcmin-1, which corresponds
to the Nyquist frequency of the effective resolution, has to be taken
with cautious.
Copyright ESO 2002