The power spectrum of an image f(x,y) of Fourier Transform
![]() is computed from the
amplitude
A(kx, ky) defined as
is computed from the
amplitude
A(kx, ky) defined as
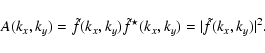 |
(A.1) |
makes an "infinite pavement'' with the image prior to compute the Fourier Transform. As the ISSA images are not periodic objects, this operation produces discontinuities where the left (top) meets the right (bottom) side of the image. These horizontal and vertical discontinuities are responsible for the cross seen in the amplitude image. The main problem with this cross is that it increases artificially the power when the average over k is done. Furthermore, the power increase is not constant as a function of k which modify the slope of the spectrum as well as the normalization.
The usual method to get rid of this effect is to apodize the image so that
the left (top) and right (bottom) sides of the image have a similar flux level.
Another method which do not modify the image but acts on the amplitude image itself is to
compute P(k) by taking the median value at constant k. For ![]() 85% of
the ISSA maps we have inspected, these two methods give very
similar results (see Fig. A.1). But when the cross is very strong,
the power at small scales is still overestimated by the "median'' method.
Furthermore, at small k values, there are less points to average and
a large fraction of them are affected by the cross effect;
at these frequencies, the median value may not be significant.
For all these reasons, we have adopted the "apodization'' method.
85% of
the ISSA maps we have inspected, these two methods give very
similar results (see Fig. A.1). But when the cross is very strong,
the power at small scales is still overestimated by the "median'' method.
Furthermore, at small k values, there are less points to average and
a large fraction of them are affected by the cross effect;
at these frequencies, the median value may not be significant.
For all these reasons, we have adopted the "apodization'' method.
Copyright ESO 2002