

Up: Rotational velocities of A-type stars
Subsections
In total, projected rotational velocities were derived for 249 B8 to
F2-type stars, 86 of which have no rotational velocities in
Abt & Morrell (1995).
The results of the
 determinations are presented in
Table 5 which contains the following data: Col. 1
gives the HD number, Col. 2 gives the HIP number, Col. 3
displays the spectral type as given in the HIPPARCOS catalogue
(ESA 1997), Cols. 4, 5, 6 give respectively the derived value of
determinations are presented in
Table 5 which contains the following data: Col. 1
gives the HD number, Col. 2 gives the HIP number, Col. 3
displays the spectral type as given in the HIPPARCOS catalogue
(ESA 1997), Cols. 4, 5, 6 give respectively the derived value of
 ,
the associated standard deviation and the corresponding number
of measured lines (uncertain
,
the associated standard deviation and the corresponding number
of measured lines (uncertain
 are indicated by a colon), Col. 7 presents possible remarks about the spectra: SB2 ("SB'') and
shell ("SH'') natures are indicated for stars showing such feature in
these observed spectra, as well as the reason why
are indicated by a colon), Col. 7 presents possible remarks about the spectra: SB2 ("SB'') and
shell ("SH'') natures are indicated for stars showing such feature in
these observed spectra, as well as the reason why
 is uncertain - "NO''
for no selected lines, ``SS'' for variation from spectrum to spectrum
and "LL'' for variation from line to line (see Appendix A).
is uncertain - "NO''
for no selected lines, ``SS'' for variation from spectrum to spectrum
and "LL'' for variation from line to line (see Appendix A).
Nine stars are seen as double-lined spectroscopic binary in the data
sample. Depending on the
 of each component, their difference
in Doppler shift and their flux ratio, determination of
of each component, their difference
in Doppler shift and their flux ratio, determination of
 is
impossible in some cases.
is
impossible in some cases.
 |
Figure 7:
Part of the spectra are displayed for the six SB2 stars that
have been observed only once: a) HD 35189, b) HD 40183,
c) HD 42035, d) HD 181470, e) HD 203439, f)
HD 203858. Three of them are well separated b), d), f), allowing
measurement of
 for both components. The three others a), c),
e) have low differential Doppler shift (
for both components. The three others a), c),
e) have low differential Doppler shift (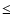 60 60
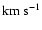 )
which makes
all the lines blended. No )
which makes
all the lines blended. No
 has been determined for these objects.
has been determined for these objects. |
 |
Figure 8:
The three following SB2 stars have been observed twice, in
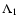 (upper panels) and
(upper panels) and 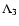 (lower panels): a)
HD 79763 at HJD 2449025, b) HD 98353 at HJD 2448274, c) HD 119537 at HJD 2449025, d)
HD 79763 at HJD 2449365, e) HD 98353 at HJD 2449413, f)
HD 119537 at HJD 2449415. SB2 nature of these objects is not
detected in
(lower panels): a)
HD 79763 at HJD 2449025, b) HD 98353 at HJD 2448274, c) HD 119537 at HJD 2449025, d)
HD 79763 at HJD 2449365, e) HD 98353 at HJD 2449413, f)
HD 119537 at HJD 2449415. SB2 nature of these objects is not
detected in 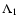 spectral range, and the derived
spectral range, and the derived
 is
a "combined'' broadening. The triple system HD 98353 is observed
close to conjunction, and lines remain blended. For HD 79763 d)
and HD 119537 f), the difference in radial velocity is large
enough to measure separately the rotational velocities.
is
a "combined'' broadening. The triple system HD 98353 is observed
close to conjunction, and lines remain blended. For HD 79763 d)
and HD 119537 f), the difference in radial velocity is large
enough to measure separately the rotational velocities. |
Table 6 displays the results for the stars in our sample which
exhibit an SB2 nature. Spectral lines are identified by
comparing the SB2 spectrum with a single star spectrum. Projected
rotational velocities are given for each component when measurable, as
well as the difference in radial velocity
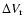 computed from a few lines in the spectrum.
computed from a few lines in the spectrum.
- 110 Tau (HD 35189) is highly suspected to be a
spectroscopic binary due to its spectra taken in the
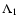 domain. As it can be seen in Fig. 7a, core of the
lines is double in most cases, corresponding to a difference in
radial velocity of about 37
domain. As it can be seen in Fig. 7a, core of the
lines is double in most cases, corresponding to a difference in
radial velocity of about 37
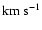 .
However, this case does not allow the measurement of the projected rotational velocity.
.
However, this case does not allow the measurement of the projected rotational velocity.
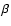 Aur (HD 40183) is a well known early A-type eclipsing binary
of Algol type. The derived
Aur (HD 40183) is a well known early A-type eclipsing binary
of Algol type. The derived
 corresponds well with the values
of Nordström & Johansen (1994) (respectively 33 and 34
corresponds well with the values
of Nordström & Johansen (1994) (respectively 33 and 34
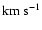 )
that indicate
synchronous rotation. Knowing the time of minimum from Johansen & Sørensen (1997):
)
that indicate
synchronous rotation. Knowing the time of minimum from Johansen & Sørensen (1997):
where E is an integer of phases,
and the Julian date of observation (HJD 2449413.3301), the phase is equal to 0.4.
- HD 42035 has no indication of any binary status in the
literature and it is flagged as a photometrically constant star from
HIPPARCOS data. Nevertheless the observed line profiles in its
spectrum tend to suggest that it is composite. The cross-correlation function (CCF) of the observed spectrum with a synthetic one
(
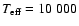 K,
K,
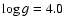 ,
,

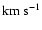 )
has been computed. This CCF is not
characteristic of a single star, and it is perfectly fitted by the
sum of two Gaussian components centered at 26 and 34
)
has been computed. This CCF is not
characteristic of a single star, and it is perfectly fitted by the
sum of two Gaussian components centered at 26 and 34
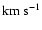 respectively and whose FWHM are 30 and 120
respectively and whose FWHM are 30 and 120
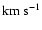 .
This indicates that the system is composed of a low
.
This indicates that the system is composed of a low
 star
and a faster rotator.
star
and a faster rotator.
- HD 79763 is known as a SB2 system whose orbital period
is P=15.986 d (Batten et al. 1989). Using the spectrum in
 range (Fig. 8d), the difference in radial velocity is sufficient to estimate
range (Fig. 8d), the difference in radial velocity is sufficient to estimate
 of both components.
of both components.
- 55 UMa (HD 98353) is a triple system for which components
are early A-type stars. Using tomographic separation, Liu et al. (1997)
estimate the
 of each of them:
of each of them: 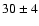
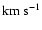 ,
,
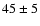
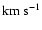 ,
,
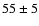
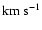 .
Knowing the orbital parameters:
P=2.5538380 d and
.
Knowing the orbital parameters:
P=2.5538380 d and
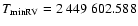 (Horn et al. 1996) for the close pair, our spectra correspond to phases
(Horn et al. 1996) for the close pair, our spectra correspond to phases
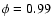 (Fig. 8b, HJD 2448274.6233) and
(Fig. 8b, HJD 2448274.6233) and
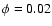 (Fig. 8e, HJD 2449413.5500). This means that
both observations were unfortunately made close to opposition, and
the difference in radial velocity is not large enough to see separated
lines. The measured
(Fig. 8e, HJD 2449413.5500). This means that
both observations were unfortunately made close to opposition, and
the difference in radial velocity is not large enough to see separated
lines. The measured
 corresponds to a blend.
corresponds to a blend.
- HD 119537 is indicated as SB in the Bright Star Catalogue
(Hoffleit & Jaschek 1982) and was not detected as a double-lined system with the spectrum collected
at ESO, within the context of the southern sample (Grenier et al. 1999;
Royer et al. 2002). The rotational velocity derived in Paper I is
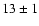
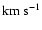 ,
whereas it equals 23.9
,
whereas it equals 23.9
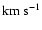 in Ramella et al. (1989). The spectrum in the
in Ramella et al. (1989). The spectrum in the 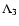 domain displays evidence of
SB2 nature and Fig. 8f shows perfectly the faint lines
around Ti II 4501, Fe II 4508 and
Ti II 4515 which are usually well isolated in a single star
with such a spectral type.
domain displays evidence of
SB2 nature and Fig. 8f shows perfectly the faint lines
around Ti II 4501, Fe II 4508 and
Ti II 4515 which are usually well isolated in a single star
with such a spectral type.
- HD 181470 is a close binary system first detected by
speckle observations by Miura et al. (1993) and later confirmed by
Hartkopf et al. (2000). The measured separation is
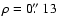 with a
magnitude difference
with a
magnitude difference
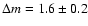 .
In the observed
spectrum, the difference in radial velocity is large: 229
.
In the observed
spectrum, the difference in radial velocity is large: 229
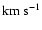 .
.
- HD 203439 is known as a spectroscopic binary system in Batten et al. (1989).
- HD 203858 is a known spectroscopic
binary. Abt & Morrell (1995) do not see the two components of the system
and give a
 which is likely overestimated, 70
which is likely overestimated, 70
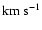 ,
because of blend
due to binarity. In this case, the components are well separated and
each
,
because of blend
due to binarity. In this case, the components are well separated and
each
 is measured.
is measured.
4.2.1 South versus North
Fourteen stars are common to both the southern sample from Paper I
and the northern one studied here. Matching of both determinations allows
us to ensure the homogeneity of the data or indicate variations intrinsic
to the stars otherwise. Results for these objects are listed in
Table 7.
Instrumental characteristics differ from ECHELEC to AURÉLIE
data. First of all, the resolution is higher in the ECHELEC spectra,
which induces a narrower instrumental profile and allows the
determination of
 down to a lower limit. Taking the calibration
relation from SCBWP as a rule of thumb (
down to a lower limit. Taking the calibration
relation from SCBWP as a rule of thumb (
![$FWHM{\scriptstyle [{\rm\AA}]} \approx
0.025~\ensuremath{v\sin i} {\scriptstyle [\ensuremath{{\rm km}~{\rm s}^{-1}} ]}$](/articles/aa/full/2002/39/aa2413/img47.gif) ), the
low limit of
), the
low limit of
 is:
is:
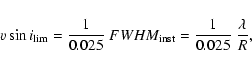 |
(4) |
where R is the power of resolution, and 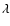 the considered
wavelength. For ECHELEC spectra (
the considered
wavelength. For ECHELEC spectra (
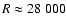 )
this limit is
6.4
)
this limit is
6.4
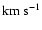 at 4500 Å, whereas for AURÉLIE data (
at 4500 Å, whereas for AURÉLIE data (
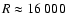 ), it reaches
11.3
), it reaches
11.3
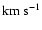 .
These limits correspond to the "rotational velocity'' associated with the FWHMof the instrumental profile. There is no doubt that in Fourier space, the
position of the first zero of a line profile dominated by the
instrumental profile is rather misleading and the effective lowest
measurable
.
These limits correspond to the "rotational velocity'' associated with the FWHMof the instrumental profile. There is no doubt that in Fourier space, the
position of the first zero of a line profile dominated by the
instrumental profile is rather misleading and the effective lowest
measurable
 may be larger. This effect explains the discrepancy found for slow
rotators, i.e. HD 27962 and HD 72660 in Table 7.
The
may be larger. This effect explains the discrepancy found for slow
rotators, i.e. HD 27962 and HD 72660 in Table 7.
The
 determination using AURÉLIE spectra is 5
determination using AURÉLIE spectra is 5
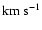 larger
than using ECHELEC spectra.
The two stars are slow rotators for which
larger
than using ECHELEC spectra.
The two stars are slow rotators for which
 has already been
derived using better resolution. HD 27962 is found to have
has already been
derived using better resolution. HD 27962 is found to have
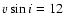 and 11
and 11
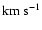 by Varenne & Monier (1999) and Hui-Bon-Hoa & Alecian (1998)
respectively. HD 72660 has a much smaller
by Varenne & Monier (1999) and Hui-Bon-Hoa & Alecian (1998)
respectively. HD 72660 has a much smaller
 ,
lower than the limit
due to the resolution of our spectra: 6.5
,
lower than the limit
due to the resolution of our spectra: 6.5
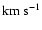 in Nielsen & Wahlgren (2000)
and 6
in Nielsen & Wahlgren (2000)
and 6
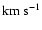 in Varenne (1999).
in Varenne (1999).
Second of all, one other difference lies in the observed spectral
domain. HD 198001 has no observation in the 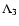 domain using
AURÉLIE, so that
domain using
AURÉLIE, so that
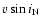 in Table 7 is not derived
on the basis of the Mg II line. The overestimation of
in Table 7 is not derived
on the basis of the Mg II line. The overestimation of
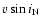 reflects the use of weak metallic lines instead the strong
Mg II line for determining rotational velocity.
reflects the use of weak metallic lines instead the strong
Mg II line for determining rotational velocity.
Using the same ECHELEC data, Grenier et al. (1999) flagged the stars according to
the shape of their cross-correlation function with synthetic
templates. This gives a hint about binary status of the stars. Three
stars in Table 7 are flagged as "probable binary or
multiple systems'' (CCF: 4 and 6).
When discarding low rotators, probable binaries and data of HD 198001 that induce biases
in the comparison, the relation between the eight remaining points is fitted
using GaussFit by:
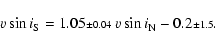 |
(5) |
Although common data are very scarce, they seem to be consistent. It
suggests that both data sets can be merged as long as great care is
taken for cases detailed above, i.e. extremely low rotators, high
rotators with no
 from Mg II line, spectroscopic binaries.
from Mg II line, spectroscopic binaries.
4.2.2 Standard stars
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2413f9}\end{figure}](/articles/aa/full/2002/39/aa2413/Timg93.gif) |
Figure 9:
Comparison of
 data for the 163 common stars between this work and
Abt & Morrell (1995). The solid line stands for the one-to-one
relation.
data for the 163 common stars between this work and
Abt & Morrell (1995). The solid line stands for the one-to-one
relation. |
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2413f10}\end{figure}](/articles/aa/full/2002/39/aa2413/Timg94.gif) |
Figure 10:
Comparison between
 data from this work and from
Slettebak et al. (1975). The solid line stands for the one-to-one
relation. The 21 standard stars are plotted with error bar on both
axes (see text). HD number of the stars that deviate most from the one-to-one
relation are indicated and these stars are listed in Table 8 and detailed in Appendix B.
data from this work and from
Slettebak et al. (1975). The solid line stands for the one-to-one
relation. The 21 standard stars are plotted with error bar on both
axes (see text). HD number of the stars that deviate most from the one-to-one
relation are indicated and these stars are listed in Table 8 and detailed in Appendix B. |
A significant part of the sample is included in the catalogue of
Abt & Morrell (1995). The intersection includes 163 stars. The
comparison of the
 (Fig. 9) shows that our determination is higher on average than
the velocities derived by Abt & Morrell (AM). The linear relation given by GaussFit is:
(Fig. 9) shows that our determination is higher on average than
the velocities derived by Abt & Morrell (AM). The linear relation given by GaussFit is:
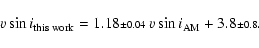 |
(6) |
Abt & Morrell use the standard stars of SCBWP to calibrate the relation FWHM-
 .
There are 21 stars in common between our sample and these standard stars.
Figure 10 displays the
.
There are 21 stars in common between our sample and these standard stars.
Figure 10 displays the
 derived in this paper
versus the
derived in this paper
versus the
 from SCBWP for these 21 common stars. The solid line represents the one-to-one relation. A clear trend is observed:
from SCBWP for these 21 common stars. The solid line represents the one-to-one relation. A clear trend is observed:
 from SCBWP are on average 20% lower. A linear least squares fit carried out with GaussFit on these values makes the systematic effect explicit:
from SCBWP are on average 20% lower. A linear least squares fit carried out with GaussFit on these values makes the systematic effect explicit:
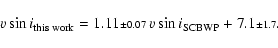 |
(7) |
The relation is computed taking into account the error bars of both sources. The error bars on the values of SCBWP are assigned according to the accuracy given in their paper (10% for
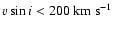 and 15% for
and 15% for
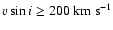 ). Our error bars are derived from the formal error found in Sect. 3.3 (Eq. (3)).
). Our error bars are derived from the formal error found in Sect. 3.3 (Eq. (3)).
Table 8:
Highlight of the discrepancy between
 values from SCBWP and ours (standard deviation of our measurement is indicated; dash "-'' stands for only one measurement). Comparison with data from the literature for the twelve stars that exhibit the largest differences.
values from SCBWP and ours (standard deviation of our measurement is indicated; dash "-'' stands for only one measurement). Comparison with data from the literature for the twelve stars that exhibit the largest differences.
 are classified in three subgroups according to the way they are derived: by-product of a spectrum synthesis, frequency analysis of the lines profiles or infered from a FWHM-
are classified in three subgroups according to the way they are derived: by-product of a spectrum synthesis, frequency analysis of the lines profiles or infered from a FWHM-
 relation independent from SCBWP's one. Flags from HIPPARCOS catalogue are indicated: variability flag H52 (C: constant, D: duplicity-induced variability, M: possibly micro-variable, U: unsolved variable, -: no certain classification) and double annex flag H59 (O: orbital solution, G: acceleration terms, -: no entry in the Double and Multiple Systems Annex).
relation independent from SCBWP's one. Flags from HIPPARCOS catalogue are indicated: variability flag H52 (C: constant, D: duplicity-induced variability, M: possibly micro-variable, U: unsolved variable, -: no certain classification) and double annex flag H59 (O: orbital solution, G: acceleration terms, -: no entry in the Double and Multiple Systems Annex).
|
Name |
HD |
Sp. type |
 (
(
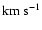 ) ) |
HIPPARCOS |
| |
|
|
SCBWP |
this
work |
depth 0pt
height 0.4pt width 3.0cm literature
depth 0pt height 0.4pt width 3.0cm |
H52 |
H59 |
| |
|
|
|
| |
spec. synth. |
freq. analysis |
FWHM |
|
|
 Gem Gem |
47105 |
A0IV |
<10 |
15 |
 |
11.2(1) |
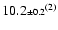 ,
19.0(3) ,
19.0(3) |
|
- |
X |
| 30 Mon |
71155 |
A0V |
125 |
161 |
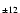 |
|
|
|
C |
- |
 UMa UMa |
95418 |
A1V |
35 |
47 |
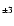 |
44.8(1), 39(4) |
44.3(3) |
|
- |
- |
 Leo Leo |
97633 |
A2V |
15 |
24 |
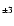 |
21(5),
22.1(1) |
24(6),
27.2(3) |
23(7) |
- |
- |
 UMa UMa |
103287 |
A0V SB |
155 |
178 |
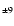 |
|
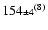 |
|
M |
- |
 Dra Dra |
123299 |
A0III SB |
15 |
25 |
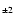 |
|
27(9) |
|
M |
O |
 Boo Boo |
128167 |
F3Vwvar |
10 |
15 |
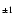 |
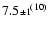 |
7.5(11) |
7.8(12),
8.1(13) |
- |
- |
 CrB CrB |
139006 |
A0V |
110 |
139 |
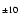 |
|
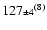 |
|
U |
O |
 Her Her |
147394 |
B5IV |
30 |
46 |
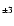 |
|
32(6) |
|
P |
- |
 Lyr Lyr |
172167 |
A0Vvar |
<10 |
25 |
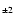 |
22.4(1),
23.2(14) |
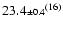 ,
24(6) ,
24(6) |
|
U |
- |
| |
|
|
|
| |
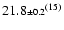 |
29.9(3) |
|
|
|
 Lyr Lyr |
176437 |
B9III |
60 |
72 |
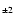 |
|
|
|
M |
- |
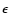 Aqr Aqr |
198001 |
A1V |
85 |
130 | - |
95(17),
108.1(1) |
|
|
- |
- |
| (1) Hill (1995). |
(6) Smith & Dworetsky (1993). |
(11) Gray (1984). |
(16) Gray (1980b). |
| (2) Scholz et al. (1997). |
(7) Fekel (1998). |
(12) Fekel (1997). |
(17) Dunkin et al. (1997). |
| (3) Ramella et al. (1989). |
(8) Gray (1980a). |
(13) Benz & Mayor (1984). |
|
| (4) Holweger et al. (1999). |
(9) Lehmann & Scholz (1993). |
(14) Erspamer & North (2002). |
|
| (5) Lemke (1989). |
(10) Soderblom (1982). |
(15) Gulliver et al. (1994). |
|
The standard stars for which a significant
discrepancy occurs between our values and those derived by SCBWP
- i.e. their error box does not intersect with the one-to-one
relation - have their names indicated in Fig. 10. They are
listed with data from the literature in Table 8 and
further detailed in Appendix B.


Up: Rotational velocities of A-type stars
Copyright ESO 2002
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2413f9}\end{figure}](/articles/aa/full/2002/39/aa2413/Timg93.gif)
![\begin{figure}
\includegraphics[width=8.8cm,clip]{MS2413f10}\end{figure}](/articles/aa/full/2002/39/aa2413/Timg94.gif)