

Up: Distant stable direct orbits
Subsections
The results obtained in the previous sections are in the framework of the restricted three-body
problem, Earth-Moon-Particle. However, the real system involves some perturbations that could
affect the stability of the regions studied. One kind of perturbation that could be relevant is the
tidal force produced by the Moon on the Earth. As a result of such force, the orbit of the Moon
evolves outward. However, the effects due to the tidal force become relevant only on relatively
large time scales. For instance, the rate at which the Moon moves away from the Earth is about 4
cm per year. Therefore, it will take about
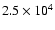 years for the orbit of the Moon to
move just one kilometer. Since we are dealing with stability on a time scale of the order of a few
years, it is reasonable to neglect the tidal effects. On the other hand, a perturbation that can
actually affect the stability regions is the solar gravitational field.
years for the orbit of the Moon to
move just one kilometer. Since we are dealing with stability on a time scale of the order of a few
years, it is reasonable to neglect the tidal effects. On the other hand, a perturbation that can
actually affect the stability regions is the solar gravitational field.
In order to investigate the effects of solar perturbations we numerically simulated and compared
two dynamical systems: the restricted three-body problem, Earth-Moon-Particle, and the restricted
four-body problem, Sun-Earth-Moon-Particle. The range of initial conditions considered covers the
area of the region h2. In fact the stable region h2 is the one that might be more useful for
practical purposes, since it is much larger than the region h1. Different from the results
presented in Fig. 2, we considered the initial conditions at pericenter at inferior
conjunction (
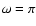 and
and 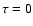 )
in order to be able to see the whole stable region of
h2 at pericenter. The time span was reduced to 103 days since that is the length of time
useful for practical purposes. In Fig. 10 we present the results in the initial
conditions frame
)
in order to be able to see the whole stable region of
h2 at pericenter. The time span was reduced to 103 days since that is the length of time
useful for practical purposes. In Fig. 10 we present the results in the initial
conditions frame 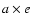 in terms of capture times.
in terms of capture times.
![\begin{figure}
\par\includegraphics[width=12.5cm,clip]{MS2168f10a.eps}\\ [3mm]
\includegraphics[width=12.5cm,clip]{MS2168f10b.eps} \end{figure}](/articles/aa/full/2002/38/aa2168/Timg32.gif) |
Figure 10:
Stability region in terms of capture times. Each initial condition has its capture
time indicated by the gray coded color. The white areas inside the gray region
correspond to initial conditions that remain captured for the whole period of integration
(103 days). Two dynamical systems were considered: a) Restricted three-body problem,
Earth-Moon-particle (top). b) Restricted four-body problem,
Sun-Earth-Moon-particle (bottom). |
The top figure corresponds to the results
on the Earth-Moon-Particle system while in the bottom figure the solar perturbation is included. A
comparison of such figures clearly show that the solar perturbation is not negligible. It reduces
the size of the stable region, whose trajectories remain captured for more than a thousand days
(white area inside the gray region). Actually, it almost divides that region into two parts.
Nevertheless, the size of the stable region is still significant. The solar perturbation reduces
the size of the stable region to about half of its size.
The effects of gravitational attraction of the Sun on the trajectories of the stable region can be
noted in two examples presented in Figs. 11 and 12.
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2168f11a.eps}\hspace*{4mm}\in...
...\hspace*{4mm}\includegraphics[width=8.8cm]{MS2168f11f.eps}\\ [5mm]
\end{figure}](/articles/aa/full/2002/38/aa2168/Timg33.gif) |
Figure 11:
Example of a trajectory with initial conditions
a=27,751.7 km and e=0.3227,
which is stable in both systems:
Earth-Moon-particle (left column), and Sun-Earth-Moon-particle (right column).
In the first row is given the trajectory in the baricentric rotating Earth-Moon system
for one thousand days. The plots of the semimajor axis and the eccentricity are given for
a time span of one hundred days, but the behaviour is the same for one thousand days.
|
![\begin{figure}
\par\includegraphics[width=8.8cm]{MS2168f12a.eps}\hspace*{4mm}\in...
...\hspace*{4mm}\includegraphics[width=8.8cm]{MS2168f12f.eps}\\ [5mm]
\end{figure}](/articles/aa/full/2002/38/aa2168/Timg34.gif) |
Figure 12:
Example of a trajectory with initial conditions
a=27,248.3 km and e=0.4638,
which is stable in both systems:
Earth-Moon-particle (left column), and Sun-Earth-Moon-particle (right column).
In the first row is given the trajectory in the baricentric rotating Earth-Moon system
for one thousand days. The plots of the semimajor axis and the eccentricity are given for
a time span of one hundred days, but the behaviour is the same for one thousand days.
|
First, it is important to
note that, as we have shown in the previous sections, the trajectories of the stable region found
in the Earth-Moon-particle system are periodic/quasi-periodic orbits. Therefore, those
trajectories will never escape, and the region is "stable for ever''. On the other hand, the
trajectories of the stable region found in the Sun-Earth-Moon-particle system are not
periodic/quasi-periodic orbits. Those are trajectories that remain captured for the whole time of
integration (103 days). So, they are stable in the sense that they do not escape. In order to
see the typical behaviour of such trajectories we chose two initial conditions that are stable in
both systems: 1)
a = 27,751.7 km and e=0.3227 (Fig. 11). 2)
a = 27,248.3 km and
e=0.4638 (Fig. 12). In the first case, Fig. 11, it can be seen that the
solar perturbation increased the amplitude of oscillation and the complexity of the evolution of
the semimajor axis and eccentricity. The trajectory in the baricentric rotating Earth-Moon system
shows a significant increase in oscillation, but it maintains a regular behaviour for one thousand
days. In the second case, Fig. 12, the solar perturbation increased the complexity of
the evolution of the semimajor axis and eccentricity, but the amplitudes of oscillation are very
close. The trajectory in the baricentric rotating Earth-Moon system shows a regular behaviour for
one thousand days and, differently from the first case, its amplitude of oscillation decreased.
Therefore, including the solar perturbations there still exists a significant region where the
trajectories show regular behaviour for at least a few years. This information can be useful in
spacecraft missions. These "stable regions'' could be used to keep missions around the Moon, at a
far distance, based on a very low fuel consumption, for at least 103 days.
Acknowledgements
This work was funded by Fapesp (Proc. 98/ 15025-7) and CNPq (Proc. 300347/01-4). These supports are
gratefully acknowledged.


Up: Distant stable direct orbits
Copyright ESO 2002
![]() years for the orbit of the Moon to
move just one kilometer. Since we are dealing with stability on a time scale of the order of a few
years, it is reasonable to neglect the tidal effects. On the other hand, a perturbation that can
actually affect the stability regions is the solar gravitational field.
years for the orbit of the Moon to
move just one kilometer. Since we are dealing with stability on a time scale of the order of a few
years, it is reasonable to neglect the tidal effects. On the other hand, a perturbation that can
actually affect the stability regions is the solar gravitational field.
![]() and
and ![]() )
in order to be able to see the whole stable region of
h2 at pericenter. The time span was reduced to 103 days since that is the length of time
useful for practical purposes. In Fig. 10 we present the results in the initial
conditions frame
)
in order to be able to see the whole stable region of
h2 at pericenter. The time span was reduced to 103 days since that is the length of time
useful for practical purposes. In Fig. 10 we present the results in the initial
conditions frame ![]() in terms of capture times.
in terms of capture times.