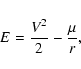 |
(1) |
In a previous paper (Vieira Neto & Winter 2001) we studied the problem of temporary gravitational capture of hypothetical satellites of Uranus. The approach adopted was to compute the capture times for a significant part of the initial condition space. One of the important features presented in the results was the regions of prisoner trajectories, trajectories that did not escape for an integration period of 105 years. Winter & Vieira Neto (2001) showed that the prisoner trajectories are actually stable trajectories. So, this approach proved to be an excellent way to detect regions of stability. In the following we describe the methodology of gravitational capture time.
The idea is based on the two-body orbital energy monitoring. The orbital energy is defined as:
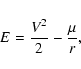 |
(1) |
Due to the perturbation of the third body (Earth), the two-body energy (Moon-particle) is not constant. By monitoring E, it is possible to have a clue of which primary has the dominant gravitational influence on the particle's trajectory. The changing of the energy's sign indicates that the osculating orbit changed from a closed orbit to an open one (escape) or from an open orbit to a closed one (capture). However, this effect is temporary and the trajectories that present a relatively large capture time (longer than the integration time) are strong candidates to be regular stable orbits.
The procedure is to explore the space of initial conditions and present the results in terms of
diagrams indicating the region explored and the initial conditions that are labeled as prisoner
trajectories. Each graphic is obtained with a grade of the semi-major axis and eccentricity,
maintaining the values of the other orbital elements constant. The orbital elements are all
relative to the Moon. The initial value of the semi-major axis, a, is chosen from 10 000 km to
50 000 km, in steps of 100 km. The eccentricity initial value, e, is chosen from 0 to 0.99, in
steps of 0.01. So, each point in the graphic corresponds to one trajectory. Moreover, each
trajectory is integrated with a negative time step from zero to -5000 days. Due to the
configuration of the initial orbital elements, the initial two-body energy has a negative value
(closed orbit). With the perturbation of the third body (the Earth), the energy changes its value.
When the value of the orbital energy changes to a positive value (open orbit) the integration is
interrupted and the time is stored. This time is called the capture time. Actually, the length of
time for a temporary capture is higher than this value. The initial conditions satisfy the mirror
theorem (Roy & Ovenden 1955) for almost all the cases considered (![]() or
or ![]() ,
where
,
where ![]() is
the argument of pericenter), which means that in those cases the precisely correct values for the
capture time are twice the values of the integration time. The integration could also stop if the
particle had a collision with the planet or the integration time surpassed 5000 days. If the
particle does not escape in the period of 5000 days its trajectory is called prisoner.
is
the argument of pericenter), which means that in those cases the precisely correct values for the
capture time are twice the values of the integration time. The integration could also stop if the
particle had a collision with the planet or the integration time surpassed 5000 days. If the
particle does not escape in the period of 5000 days its trajectory is called prisoner.
Figure 2 shows a diagram of the initial conditions in terms of a versus e.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{MS2168f03.eps} \end{figure}](/articles/aa/full/2002/38/aa2168/Timg14.gif) |
Figure 3:
Set of Poincaré surfaces of section for different values of Jacobi constant,
|
We also explored regions of the initial condition space for prograde orbits at pericenter for a
range of values of the argument of pericenter,
![]() ,
with
,
with
![]() .
No
other region of prisoner trajectories was found for such values of
.
No
other region of prisoner trajectories was found for such values of ![]() .
.
Copyright ESO 2002