3 Average spectrum and emission lines variations

The mean normalized spectrum of IP Peg, based on first dataset, is shown in Fig. 1. The mean spectrum for second dataset can be found in Wolf et al. (1998, Fig. 2). Before averaging the single spectra were shifted according to the $K_{1}\sin(\phi)$, with K₁ = 168 km s^-1 (Wolf et al. 1998). For the calculation of orbital phases the ephemeris of Wolf et al. (1993) was used:

$$T_{0}(HJD) = 2445615.4156 + 0.15820616 \cdot E,$$

where T₀ is the moment of mid-eclipse.

Both spectra show strong, broad hydrogen and helium emission lines. The trailed spectra of the major hydrogen lines are shown in Fig. 2 (note that the data are displayed twice for clarity). Their double-peaked profiles are thought to be associated with the accretion disk. They are superposed by asymmetric structures produced by anisotropically radiating emission regions of the binary system. The line profiles demonstrate a puzzling behaviour the blue-shifted peak being stronger than the red-shifted peak when averaged over the orbit.

Figure 3: The degree of asymmetry of the emission line H$\beta$ folded with the orbital period (top panel: first dataset, bottom panel: second dataset). The degree of asymmetry is the ratio between the areas of violet and red peaks of the emission line. The data are plotted twice for continuity.

Figure 4: Some profiles of the H$\beta$ line which show the rather considerable asymmetry of its wings. It can be seen that from time to time on blue and red wings a hump appears.

We have measured the degree of asymmetry of each line profile, and have plotted this parameter against the orbital phase (in the following this plot is named: the S-wave graph). We have calculated the degree of asymmetry S as the ratio between the areas of violet and red peaks of the emission line. Let us highlight the principal features of the resulting curves (Fig. 3). Note first that their shape obviously deviates from of a sine wave, although for an accretion disk with a single bright spot it should be nearly sinusoidal (Borisov & Neustroev 1998). In addition to this, the amplitude of this intensity variation of the blue peak exceeds by far that for the red peak. However, it can be seen that the degree of asymmetry with S > 1 is observed only during one-half of the orbital period, whereas $S \leq 1$ is found at other times. The possible reasons for such variations of the degree of asymmetry can be an anisotropic radiation of the bright spot and/or an eclipse of the bright spot by the outer edge of the accretion disk. These assumptions will be discussed in the course of further analysis.

A closer inspection of the line profiles shows that all the emission lines exhibit a considerable asymmetry of their wings which varies with time. This effect is observed in both data sets but most notably in the first one. The visual analysis has shown that from time to time a hump appears on the blue and red wings (Fig. 4). Its shift concerning the center of the line does not exceed $\sim$1200-1400 km s^-1.

To describe the wing asymmetry WA quantitatively, we define the following quantity:

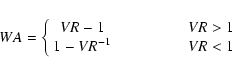$$WA = \left\{ {\begin{array}{*{20}c} {VR - 1} & {\begin{array... ...space{1.5cm} VR < 1} \\ \end{array}} \\ \end{array}} \right.$$ (1)

where

$$VR = {{\sum\nolimits_{\lambda_0 - {\rm d}\lambda }^{\lambda_0... ...lambda_0 + ({\rm d}\lambda + \Delta\lambda )} {I_\lambda } }}.$$

Here ${\lambda_0 }$ is the wavelength of the center of the line, and d${\lambda}$defines the beginning of the wavelength interval  ${\Delta\lambda}$in which the fluxes are summed up.

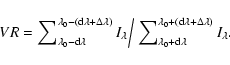
To see how the wing asymmetry of the emission lines depends on time, we calculated the degree of the wing asymmetry of all H$\beta$ profiles and plotted their values against the time of observations (Fig. 5, upper left panel). In this case we have used following parameters: d ${\lambda} = 15$ Å and ${\Delta\lambda} = 10$ Å. It can be seen that the wing asymmetry shows quasi-periodic modulations with a period much shorter than the orbital one. This indicates the presence of an emission source rotating asynchronously with the binary system.

We looked for periods in this data sample using the Scargle (1982) method and tested our results using the AoV method (Schwarzenberg-Czerny 1989) and the PDM algorithm (Phase Dispersion Minimization, Stellingwerf 1978).

The calculated periodogram shows three strong peaks at 0 $.\!\!^{\rm h}$61, 0 $.\!\!^{\rm h}$33 and 1 $.\!\!^{\rm h}$67, the first one being little bit stronger of them (Fig. 5, lower left panel). This result was confirmed applying the AoV and PDM methods. As an example we have fitted the wing asymmetry's data from Fig. 5 (upper left panel) by a simple sinusoid with the period of 0 $.\!\!^{\rm h}$61 and have plotted this curve by a dotted line in the same figure.

A detailed discussion of the line-wings' variations is given in Sect. 5.

Figure 5: In the upper left panel is shown the degree of the wing asymmetry of the emission line H$\beta$ from the first dataset plotted against the time of observations. These data have been fitted by the simple sinusoid with the period 0 $.\!\!^{\rm h}$61 (dotted line). In the lower left panel the periodogram of the above data is shown. The periodogram shows three strong peaks at 0 $.\!\!^{\rm h}$61, 0 $.\!\!^{\rm h}$33 and 1 $.\!\!^{\rm h}$67, the first one is the little bit stronger of them. In the right-hand column are shown some profiles of the H$\beta$ line in which the wavelength range used for the determination of the degree of the wing asymmetry has been marked.