Appendix B: Segment Cox processes

We used the segment Cox point process (see Stoyan et al. 1995) to model the correlation properties of our observational samples. This process is constructed as follows: segments of length l are randomly generated inside a cube of size L (a Poisson distribution of starting points and a uniform distribution of directions in space) and Poisson-distributed points are generated along these segments. The second parameter we have to choose after l is the intensity (mean density) of segments $\lambda_{\rm S}$. Then the length density of all segments $L_{\rm V}$ is defined as

$$\begin{eqnarray*}L_{\rm V}=\lambda_{\rm S} L. \end{eqnarray*}$$

The last parameter we have to choose in order to specify the process is the line intensity of points $\lambda_{\rm L}$. The intensity of the point process $\lambda$ is

$$\begin{eqnarray*}\lambda=\lambda_{\rm L} L_{\rm V}=\lambda_{\rm L}\lambda_{\rm S} l. \end{eqnarray*}$$

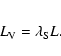
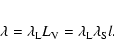
Although this distribution of points might seem rather artificial, the good news is that the pair correlation function $\xi(r)$ for this process is known exactly (Stoyan et al. 1995):

$$\xi(r)=\left\{ \begin{array}{r@{\quad}l} \frac{\displaystyl... ...style rl}\Big), &x\le r_0,\\ 0,&x>r_0. \end{array} \right.$$ (B.1)

As we can see, the correlation function depends on r as $\xi(r)\sim(r/r_0)^{-2}$for small r. This makes it suitable for modeling observed clustering of galaxies and galaxy clusters. It does not depend on the intensity $\lambda_{\rm L}$ at all. Also, the process is homogeneous on large scales by construction. We illustrate the correlation function in Fig. B.1.

Figure B.1: The correlation function of a segment Cox process for different correlation amplitudes.

If we want to simulate a cosmological sample, we are usually given the sample size L, the correlation length r₀ and the number of objects in the sample. How do we choose the parameters $l,\lambda_{\rm S}$ and $\lambda_{\rm L}$ that describe a segment Cox process?

First, we have to choose the segment length l. It certainly has to be larger than r₀ and can be chosen by the location of the first zero of the observed correlation function. Also, as seen in Fig. B.1, the smaller the ratio r₀/l, the better is the approximation $\xi(r)\sim r^{-2}$. This, however, frequently gives too large a value for d. A large d means that the intensity of segments will be small and their total number $N_{\rm S}=\lambda_{\rm S} L^3$ will be small, too; we get a rather unrealistic distribution of points along a few long segments.

On the other hand, if we do not worry too much about the exact slope of the correlation function, we could choose l rather close to r₀ (the upper curve in Fig. B.1). We have found that taking $l\approx1.5r_0$ works well in practice.

Let us say that we have decided to choose $l=\alpha r_0$. Then, formula (B.1) for the correlation function tells us that

$$\begin{eqnarray*}L_V=\frac{1}{2\pi r_0^2}\left(1-\frac{1}{\alpha}\right). \end{eqnarray*}$$

We obtain for the intensity (mean density) of the segments:

$$\begin{eqnarray*}\lambda_{\rm S}=L_{\rm V}/d, \end{eqnarray*}$$

and the last parameter $\lambda_{\rm L}$:

$$\begin{eqnarray*}\lambda_{\rm L}=\frac{N}{L^3 L_{\rm V}}\cdot \end{eqnarray*}$$

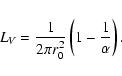
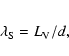
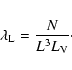
An important point to remember when generating a segment Cox process is that having a mean number of segments $N_{\rm S}=\lambda_{\rm S} L^3$does not mean that we have to generate $N_{\rm S}$ segments. The number of segments is a Poisson-distributed random number with intensity (mean) $N_{\rm S}$, and it is useful to recall that its variance is also $N_{\rm S}$. So every realization will give us a different number of segments. The same concerns the number of points on the segments. All this combines to give us a different total number of points with every realization.