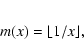
Regularity periodograms for constant density cubes can be found analytically, counting regions of different density generated by partially filled period cells at the boundaries. This is effectively a description of edge effects.
We found these expressions useful when debugging our code. Moreover, we discovered that our original estimator was biased, by comparing the results of our program with the analytic formula.
As this method can be used in a similar way also for 2-D and 1-D cubes (squares and line segments), we give formulae for these cases, too.
We shall use two auxiliary functions below:
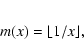
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h1676f34.eps}\end{figure}](/articles/aa/full/2002/37/aah1676/Timg164.gif) |
Figure A.1: Periodograms for uniform density cubes (using the full estimator), for 1D, 2D and 2D cases. The full period range is shown. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h1676f35.eps}\end{figure}](/articles/aa/full/2002/37/aah1676/Timg165.gif) |
Figure A.2: Periodograms for uniform density cubes (using the estimator that discards local correlations), for 1D, 2D and 2D cases. |
The formulae:
3-D, all points:
![\begin{eqnarray*}\kappa_{3D}(y)&=&y^3\big\{[y-v(y)]^3 m^6(y)\\
&&+{}3v(y)[y-v(...
...t]^2\\
&&+{}v^3(y)\left[m^3(y)+3m^2(y)+3m(y)+1\right]^2\big\};
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img166.gif)
![\begin{eqnarray*}\kappa'_{3D}(y)&=&y^3\big\{[y-v(y)]^3 m^3(y)\left[m^3(y)-1\righ...
...+1\right]\\
&&\times{}\left[m^3(y)+3m^2(y)+3m(y)\right]\big\};
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img167.gif)
2-D, all points:
![\begin{eqnarray*}\kappa_{2D}(y)&=&y^2\big\{[y-v(y)]^2 m^4(y)\\
&&+{}2v(y)[y-v(...
...y)\right]^2\\
&&+{}2v^2(y)\left[m^2(y)+2m(y)+1\right]^2\big\};
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img168.gif)
![\begin{eqnarray*}\kappa'_{2D}(y)&=&y^2\big\{[y-v(y)]^2 m^2(y)\left[m^2(y)-1\righ...
...y)+2m(y)+1\right]\\
&&\times{}\left[m^2(y)+2m(y)\right]\big\};
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img169.gif)
![\begin{eqnarray*}\kappa_{1D}(y)&=&y\{[y-v(y)]m^2(y)\\
&&+{}v(y)[m(y)+1]^2\};
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img170.gif)
![\begin{eqnarray*}\kappa'_{1D}(y)&=&y\{[y-v(y)]m(y)[m(y)-1]\\
&&+{}v(y)[m(y)+1]m(y)\}.
\end{eqnarray*}](/articles/aa/full/2002/37/aah1676/img171.gif)
The amplitudes of both estimators (edge effects) grow with dimension. Nevertheless the second estimator that discards local correlations, also reduces the edge effects considerably.
Copyright ESO 2002