We shall use in this study the 1999 version of the compilation by Andernach & Tago (1998) of all published galaxy redshifts towards galaxy clusters in the catalogue of rich clusters of galaxies by Abell (1958) and Abell et al. (1989) (hereafter Abell clusters). The 1999 version of the compilation will be described in detail elsewhere (Einasto et al. 2001). Individual galaxies were associated with a given Abell cluster if they lay within a projected distance of $\leq$ 1.5 h^-1 Mpc (one Abell radius) and within a factor of two of the redshift estimated from the brightness of the clusters 10th brightest galaxy, using the photometric estimate of Peacock & West (1992). For the present analysis we used a sample of all rich clusters (richness class $R \ge 0$ and excluding clusters from ACO's supplementary list of S-clusters) in this compilation with redshifts up to z=0.13. The sample contains 1665 clusters, 1071 of which have measured redshifts for at least two galaxies. Distances of clusters without measured redshifts and of clusters with only one galaxy measured have been estimated on the basis of the apparent magnitude of the 10th brightest galaxy of the cluster. The spatial distribution (in supergalactic coordinates) of the sample is shown in Fig. 12. The Galactic zone of avoidance breaks the distribution into two cones. The slight inclination of the cones with respect to the coordinate axes is due to the $6.3^\circ$ angle between the supergalactic Y axis and the Galactic North Pole.

As representatives of high-density regions in the Universe we used rich superclusters from the list of superclusters presented in Paper I. Superclusters were identified using the friend-of-friends algorithm (used first in studies of large-scale structure by Zeldovich et al. 1982) with a neighbourhood radius of 24 h^-1 Mpc. In this way all clusters of a supercluster have at least one neighbour at a distance not exceeding the neighbourhood radius. To illustrate the distribution of clusters in high-density regions we plot in Fig. 13 only clusters in rich superclusters, while in the quantitative analysis below we shall use both the sample shown in the figure and the full cluster sample. The sheets plotted are 300 h^-1 Mpc thick, thus some superclusters overlap in projection. The sheet in the left panel of Fig. 13 crosses the majority of the cells of the supercluster-void network present in our cluster sample; the sheet in the right panel contains all clusters of the sample in the southern Galactic hemisphere. Figure 13 shows clearly the quasi-regular network of superclusters interspersed with voids. The three-dimensional distribution of all Abell and APM clusters in rich superclusters in the whole volume within a limiting radius 350 h^-1 Mpc around us can be viewed at the home page of Tartu Observatory (http://www.aai.ee).

$\begin{figure} \par\includegraphics[width=18cm,clip]{h1676f16.eps}\end{figure}$

Figure 13: Distribution of clusters in high-density regions in supergalactic coordinates. The left panel shows the clusters within a sheet, limited by $-100 \leq X \leq 200$ h^-1 Mpc (in supergalactic coordinates). Abell and APM clusters in superclusters with at least 8 or 4 members are plotted with symbols as indicated. The supergalactic Y=0 plane coincides approximately with the Galactic equatorial plane and marks the Galactic zone of avoidance. In the right panel only clusters in the southern Galactic hemisphere are plotted; here the depth is $-350 \leq Y \leq -50$ h^-1 Mpc.

For comparison we plot in Fig. 13 also the distribution of the APM clusters of galaxies in rich superclusters. We see that the APM cluster sample covers a much smaller volume in space which makes it difficult to investigate the regularity of the distribution of high-density regions on large scales. The APM cluster sample is defined only in the southern Galactic hemisphere, and even here the APM sample containing clusters with measured redshifts covers only three high-density regions defined by very rich superclusters with at least 8 cluster members. These are the Sculptor (SC9), Pisces-Cetus (SC10), and Horologium-Reticulum (SC48) superclusters of the catalogue in Paper I. To investigate the regularity of the supercluster-void network, the sample volume must exceed the period of the network at least several times. For this reason we have used only Abell clusters in the following analysis.

Using the friend-of-friends algorithm, we generated from the full catalog (ACO1) catalogs of clusters belonging to superclusters with at least 2 members (ACO2), at least 4 members (ACO4) and at least 8 members (ACO8). As the strongest regularity was observed in the ACO8 sample, we concentrated our studies on that sample and compared it with the full cluster sample. We also studied separately the northern and southern (with respect to Galactic coordinates) half-cones ACO1N, ACO1S, ACO8N and ACO8S.

3.2 Reference samples

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f17.eps}\end{figure}$

Figure 14: Determination of the radial selection function for the ACO8 sample with 373 clusters. Crosses show the observed radial distribution. The solid line (marked F) is the fitted selection function found, and the dashed line (marked n) is the spatial number density derived from the selection function, rescaled to fit in the same plot.

In order to eliminate the influence of the sample geometry and of selection effects we have to construct reference samples with the same geometry and selection function as those observed. As the regularity test is sensitive to small cubic signals, considerable care has to be taken when building reference samples.

We started with determining the selection functions for all samples we used in the analysis. As the main sources that determine the observability of a cluster are its distance and Galactic obscuration that are independent of each other, the selection function F(r,b) (r is the distance and b is the Galactic latitude) can be represented as a product of two selection functions, F_r(r) and F_b(b). We delineate our procedure on the example of the radial selection function F_r(r).

We started by building an integral probability distribution F_r(r) of cluster distances - ordering all r_i (the distance to the ith cluster) by their values and forming a step function with the increment 1/N (where N is the total number of points in the sample). We then found a least-squares polynomial fit to this distribution. Checking the form of the approximation and its derivative (which is equal to the spatial density multiplied by r²), we chose the order of the approximation and the upper and lower boundaries $r_{\min}$ and $r_{\max}$ for the distribution.

This procedure is illustrated in Fig. 14 for the radial selection function for the ACO8 sample. The number of clusters in that sample is fairly small (373) and binning this number would not be useful. The radial distribution is rather lumpy, too, as seen from the wiggles in the observed probability distribution, shown with crosses in Fig. 14. The polynomial approximation smoothes these wiggles out nicely. The density distribution obtained from that function is also shown in the Figure.

**Table 1:** Coefficients of the selection functions (columns a₀, a₁, a₂, a₃, a₄) and the coordinate ranges (d₁, d₂).
F(x)=a₀+a₁x+a₂x²+a₃x³+a₄x⁴,
$F_{\min}=F(d_1), F_{\max}=F(d_2)$ .
Data	type	a₀	a₁	a₂	a₃	a₄	d₁	d₂
ACO1	sinb	0.181088	-1.53176	3.59138	-1.53302	0.292309	0.26	1
ACO1N	sinb	0.0760189	-0.860193	2.57105	-0.786879	0	0.19	1
ACO1S	sinb	0.107172	-0.718337	0.75158	1.88259	-1.023	0.28	1
ACO1	r	-0.00981878	-0.000147744	3.70636e-06	1.32363e-08	0	65.2	355.4
ACO1N	r	-0.0820001	0.00135584	-4.48581e-06	2.59908e-08	0	70.2	355.4
ACO1S	r	0.0615636	-0.00172044	1.19554e-05	8.86643e-10	0	72.0	355.4
ACO8	sinb	0.392894	-2.0418	2.6489	0	0	0.4	1
ACO8N	sinb	-0.12838	0.908411	-2.45742	2.67739	0	0.33	1
ACO8S	sinb	-0.5535	0.337642	1.21586	0	0	0.55	1
ACO8	r	0.076307	-0.00274636	2.65024e-05	-3.21016e-08	0	60.0	353.7
ACO8N	r	-0.717997	0.0111047	-3.97325e-05	6.23955e-08	0	89.1	353.7
ACO8S	r	-0.334387	-0.00102197	2.72916e-05	-3.87503e-08	0	151.0	352.7

Will smoothing of the selection functions introduce an artificial regularity signal? It is natural to assume that selection functions should be monotonic functions of their arguments, and the wiggles in the observed probability distribution are caused by real inhomogeneous large-scale structure. A regular cubic alignment will certainly introduce slight irregularities in the radial distribution of clusters. An attempt to exactly mimic these wiggles in the reference sample would introduce a specific undesirable regularity there. Thus we shall use reference samples with smooth radial and angular density distributions.

The last step is a linear transformation that ensures that the fitted function satisfies strictly the conditions $F_r(r_{\min})=0$ and $F_r(r_{\max})=1$ :

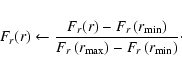
We proceeded in a similar way for the angular selection function. As found before (Einasto et al. 1997d), it can be best approximated as a distribution of $\sin(b)$ .

When generating the reference samples, we used ten times more particles than in the observed samples to avoid the shot noise from normalization. As we know the integral distribution functions, generation of the random reference samples is straightforward. We generate a uniform random number $f \in [0,1]$ and solve the equation F_r(r)=f for r. Then we select another f and solve the equation $F_{{\rm sinb}}(\sin b)=f$ for $\sin(b)$ , select a uniformly distributed Galactic longitude $l\in[0,2\pi]$ and place our point.

We fitted selection functions for each sample separately, as the spatial effects of the procedures used to select clusters for different samples are difficult to quantify.

The coefficients of the selection functions and the coordinate limits are given in Table 1.

3.3 Regularity analysis

Although we should search first for the best orientation of our cubic alignment, we rely on our visual impressions that tell us that the distribution of clusters in high-density regions looks fairly regular when seen in supergalactic coordinates (see Fig. 13). Thus we shall study the orientation problems later and suppose now that the best orientation is just along supergalactic SGX,SGY,SGZ. We shall learn that this is not a bad assumption at all.

Let us turn first to the analysis of the full sample. The (reduced) regularity periodogram for that sample is shown in Fig. 15 and the periodograms for the sub-cones in Fig. 16. In all these figures the periodogram is shown along with the confidence regions obtained from 100 Poisson models with the same number of clusters, same geometry and same selection functions as those of the observed sample. Dotted lines show the 99% and 80% confidence regions.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f18.eps}\end{figure}$

Figure 15: Regularity periodogram for the full cluster sample (solid line). Dotted lines show the 80% and 90% confidence regions.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f19.eps}\par\includegraphics[width=8.8cm,clip]{h1676f20.eps}\end{figure}$

Figure 16: Regularity periodograms for the northern sub-cone of the full cluster sample (upper panel), and for the southern sub-cone of the full cluster sample (lower panel). Periodograms are shown with solid lines, the 80% and 90% confidence regions with dotted lines.

We see that the regularity periodogram shows a clear signal on scales of 130 h^-1 Mpc and 220-240 h^-1 Mpc. If the distribution contained an ideal cubic signal, the second peak (the first sub-harmonic) should have been at 260 h^-1 Mpc, but there is none. The first harmonic, if it exists, has a bit too large a period of $\sim$ 75 h^-1 Mpc. The widening of the confidence regions at $\sim$ 350 h^-1 Mpc is due to the double-cone geometry of the sample, given that 350 h^-1 Mpc is the characteristic size of both cones.

Analysis of separate cones allows us to see where the regularity signal comes from. So, the northern cone (Fig. 16, upper panel) supports both the 130 h^-1 Mpc peak (rather weakly) and the 260 h^-1 Mpc peak (note the exact match of the two periods) but the southern cone (Fig. 16, lower panel) supports only the 130 h^-1 Mpc peak (and its harmonic, the 65 h^-1 Mpc peak can be seen here, too). Surprisingly, the expected 260 h^-1 Mpc signal is practically absent in the southern cone. Thus there seems to be a good regularity signal from both cones, but joining them together mixes the periods and amplitudes.

As suggested by correlation analysis (Tago et al. 2000), the subsample of clusters from dense regions (ACO8) should be especially regular. The regularity periodograms for that sample are shown in Figs. 17, 18 and 19.

The double-cone sample (ACO8) shows a very strong signal at 140 h^-1 Mpc, the first harmonic at 60-70 h^-1 Mpc, a signal at 225 h^-1 Mpc and another at 340 h^-1 Mpc. The latter is probably due to an extremely inhomogeneous nature of the distribution that is difficult to model correctly. The surprise comes from the northern cone (Fig. 18), where only a 60-70 h^-1 Mpc period can be seen, moreover at a low confidence level. For most of the periods this sample is more uniform than the Poisson one (this is no surprise, in principle, as Poisson distributions are not too uniform). Such a uniformity could be the side effect of our recipe that discards nearby points in real space when estimating densities.

The southern cone of the ACO8 sample shows a pronounced regularity signal, although at a slightly larger period than expected, at 140 h^-1 Mpc. The first harmonic at 70 h^-1 Mpc is also clearly seen. The small size of the sample prevents the search for sub-harmonics.

3.4 Low-dimensional regularities

The first indications of large-scale periodicity in the distribution of galaxies and clusters were found by Broadhurst et al. (1990). The period they found was along a pencil beam and thus a one-dimensional regularity with a period in the range of those we are seeing here. A periodic signal along two axes, or a single axis of a cube will be detected by the regularity periodogram as a cubic signal, too, only of a lower amplitude. Thence we have to check whether the periods seen in the periodograms above really imply a cubic network.

The approach we used can be easily modified to be applied to 2-D and 1-D "cubes''. For this purpose the points (clusters) have to be projected either on a coordinate plane or on a coordinate axis, and the kernel has to be modified accordingly. This needs only slight modifications of the programs. We performed this exercise for the ACO8 sample of clusters in dense regions and its southern sub-cone ACO8S. Given that the periodicity discovered by Broadhurst et al. (1990) was observed towards the Galactic poles and this direction is very close to the supergalactic Y-axis, we performed the 1-D analysis along this axis and the 2-D analysis for the supergalactic X-Z plane.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f21.eps}\end{figure}$

Figure 17: Regularity periodogram for the subsample of clusters from dense regions (ACO8, solid line). Dotted lines show the 80% and 90% confidence regions.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f22.eps}\end{figure}$

Figure 18: Regularity periodogram for the northern sub-cone of the ACO8 cluster sample (solid line). Confidence regions are as above.

These 2-D and 1-D results are shown in Fig. 20. The periodogram for the full sample shows rather weak one-dimensional periodicity. The sequence of periods ( $\sim$ 65 h^-1 Mpc, $\sim$ 130 h^-1 Mpc, $\sim$ 210 h^-1 Mpc) indicates that $\sim$ 65 h^-1 Mpc seems to be the main period in the supergalactic Y-direction.

The 2-D periodicity is stronger and clearer. However, the 1-D and 2-D periods are not well correlated. The rapid growth of the 2-D signal at 300 h^-1 Mpc is probably a normalization effect.

The 2-D and 1-D periodograms for the ACO8S sample are closer to each other, although they are also shifted relative to each other. The small volume of this sample does not allow us to search for larger periods.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f23.eps}\end{figure}$

Figure 19: Regularity periodogram for the southern sub-cone of the ACO8 cluster sample (solid line). Confidence regions are as above.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f24.eps}\par\includegraphics[width=8.8cm,clip]{h1676f25.eps}\end{figure}$

Figure 20: Low-dimensional regularity periodograms for the ACO8 sample. The solid line show 1-D regularity along the supergalactic Y-axis (along the Galactic poles) and the dashed lines shows 2-D regularity in the X-Z plane. The upper panel shows the periodogram for the full sample and the lower panel for the southern ACO8S subsample.

We conclude from this analysis that although the main cubic signal comes from the distribution of rich clusters in the supergalactic X-Z plane, there is a substantial contribution from the perpendicular direction, too. This is, however, smaller than could be expected from the clear periodicity observed by Broadhurst et al. (1990) in that direction. And, as before, we see that the main source of this signal is the southern sample of clusters belonging to rich superclusters.

3.5 Search for the best alignment

The results presented above tell us that there is a clear regularity in the distribution of clusters of galaxies (especially those from high-density regions) when the trial cubes are aligned along supergalactic coordinates. Is this the best orientation, or are there other preferred alignments, too?

A cube is a solid body and so its orientation in space (with respect to a fixed coordinate system) is described by three Euler angles. We have chosen the following convention for these angles: 1) $\alpha$ is the angle of rotation of the cube around the z-axis, 2) $\beta$ is the angle of rotation around the resulting y-axis of the cube and 3) $\gamma$ is the angle of rotation around the resulting z-axis of the cube. The first two angles determine the direction of the new z-axis and the last one rotates the cube around the latter. Because of the cubic symmetry all the possible alignments are described by the range of angles $\alpha,\beta,\gamma\in[0,90^\circ]$ . As we have to compute a full periodogram for every combination of the Euler angles, the full parameter space is 4-dimensional.

So far our analysis was one-dimensional, the only parameter we varied was the trial period d. This is similar to the conventional case of isotropic statistics, which depend only on the distance r. In contrast to that, the search for special spatial arrangements is much more difficult and time-consuming. In our case, we had to search the 4-dimensional parameter space, and this formed the main amount of work done in this study.

To start, we have also to quantify what we mean by a "better periodogram''. The maximum amplitude of a periodogram is probably not the best candidate for that - in the periodograms shown above we have seen examples when periodograms grow at large d because of insufficient compensation for edge effects. We would like to see well-separated maxima in periodograms, and we can quantify that by doing a discrete wavelet decomposition of a periodogram and choosing the maximum wavelet amplitude to describe the periodogram. Since the wavelet decomposition represents a function as a sum of localized "peaks'' (see, e.g. Press et al. 1997), the result should be close to our expectations. Our experience has shown that in almost all cases we studied it corresponded to our notion of the best periodogram. An example of the procedure is shown in Fig. 21.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f26.eps}\end{figure}$

Figure 21: Two regularity periodograms (upper panel) and their wavelet decompositions (lower panel). The "better'' periodogram is shown by solid line in both panels. The wavelet amplitudes of the second (dashed line) periodogram in the lower panel are slightly shifted in the wavelet index n.

We used the fast discrete wavelet transform from Press et al. (1997) with the simplest Daubechies 4-coefficient wavelet filter. We tried also the "Mexican hat'' wavelet, but the results were similar. As the fast wavelet transform requires a data vector of a length equal to a power of 2 and supposes that this vector is periodic, we padded the remainder of our periodogram, interpolating linearly between its first and last points. This should diminish the amplitude of the first wavelet coefficient; to be on the safe side, we ignored this coefficient when finding the maximum amplitude, anyway. Given that the positive amplitude of basis wavelet functions is usually larger than the negative amplitude (this is certainly the case with the Daubechies wavelet we used), we chose the maximum wavelet transform amplitude as a result, not the maximum absolute magnitude.

As seen in Fig. 21, when comparing the two slightly different periodograms, the better periodogram gives a larger maximum wavelet amplitude, as expected. Since the padding procedure expanded the periodogram range to 512 h^-1 Mpc (256 steps of 2 h^-1 Mpc resolution), the scale of this (4th) amplitude is 128 h^-1 Mpc, and corresponds to the $\sim$ 130-140 h^-1 Mpc peak in the upper panel.

Having replaced a periodogram by its amplitude (let us denote it by A), we have reduced our problem of period search to a 3-D cube of Euler angles that is easier to manage. We used for the period search the Powell algorithm described in Press et al. (1997) and the algorithm from that book. However, as we cannot suppose that the function $A(\alpha,\beta,\gamma)$ has only one (local) maximum, we have to explore first the full cube of Euler angles and to find the coordinates for the starting points for our search.

The computation of A for that cube is rather time-consuming. We computed a cube with a $5^\circ$ resolution; it took about a full day on an SGI Origin 200 for the largest ACO1 cluster sample. We also computed only the unreduced periodogram, as otherwise the computational time would have grown too large. As the periodogram for the reference sample is fairly smooth, that probably did not change much the local properties of the amplitude field.

In order to better see local maxima, we then generated an inhomogeneous Poisson point field in the Euler cube with a density of

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f27.eps}\end{figure}$

Figure 22: An inhomogeneous Poisson point process for the cube of Euler angles. The high-density clumps show the local maxima of the wavelet amplitude of the regularity periodogram for the ACO8S sample.

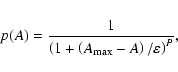
The coordinates of the densest clusters of points in the Euler cube are approximate solutions for the best orientation periodograms. In order to obtain the final solutions, we used the Powell algorithm. The periodogram interval for the search was limited to d=260 h^-1 Mpc in order to avoid possible normalization effects. Usually the final location of the maximum remained close to the initial one; the change was in most cases less than $10^\circ$ in every coordinate.

The most crowded cluster of final solutions for the Euler angles for the ACO8S sample was close to $(\alpha,\beta,\gamma)= (6^\circ,3^\circ,0^\circ)$ with a scatter of about $2^\circ$ . The effect of that rotation is to bring the Y-axis closer to the direction to the (northern) Galactic pole (the angle between the supergalactic Y-axis and the Galactic pole is $6.3^\circ$ ). This gave also the maximum amplitude for the 140 h^-1 Mpc peak of the periodogram. We illustrate this in Fig. 23. We do not show confidence limits on periodograms here and below to avoid crowding; they are similar to those shown in Figs. 15 to 19.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f28.eps}\end{figure}$

Figure 23: Maximum amplitude periodograms for the ACO8 and ACO8S samples. The low amplitude periodograms are for ACO8, the high amplitude pair is for ACO8S. Dotted lines describe the cubic grid aligned with supergalactic coordinates, solid lines - the best solutions.

As we see, the solution is better, but not much; for the full ACO8 sample the improvement is minimal, mainly in the amplitude of the second sub-harmonic.

We show the best solutions for the ACO8S sample in Fig. 24, with the very best solution labelled as "1''. The Euler coordinates for other solutions are given in Table 2. As we see, all other acceptable periodograms have considerably smaller amplitudes than the solution aligned approximately along the supergalactic coordinate axes. Some of the acceptable solutions in Fig. 24 also display shorter main periods, starting from 110 h^-1 Mpc. The 130 h^-1 Mpc periodicity favored in our previous papers can be seen here too at a rather high amplitude.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f29.eps}\end{figure}$

Figure 24: The best periodograms (local maxima) for the ACO8S sample. The curve labeled "1'' is the overall best solution. The Euler angles for all periodograms are given in Table 2.

The best solution for the full ACO8 sample, also shown in Fig. 23, has a sightly different alignment than that for the ACO8S cone: ( $10.1^\circ, 10.1^\circ, 81.9^\circ$ ); the last rotation is equivalent to $\gamma=-8.9^\circ$ . This reduces mainly to the rotation by $\sim$ $10^\circ$ around the supergalactic Y-axis. This solution has a period of 130 h^-1 Mpc, and the 260 h^-1 Mpc sub-harmonic is also clearly seen.

All searches for the best solutions converged to that solution or to the other three solutions, which are listed in Table 2. In contrast with the ACO8S subsample, these solutions have amplitudes similar to the best solution. Rather than single well-defined periods there are whole ranges of acceptable periods.

The best solutions for the full sample are all of similar amplitude. They display a variety of periods, one of these always in the range 120-140 h^-1 Mpc, as we have found for previous samples. The Euler angles for the solutions are given in Table 2. The total number of points in the signal can be estimated by formula (9), supposing that the filling factor of the structure is around 0.3. Using the amplitude $\sim$ 0.06 of the best periodogram for the sample ACO1, we obtain $\sim$ 0.13 for S/N, or $\sim$ 200 points for the signal. The number of clusters in sample ACO8S, where most of the signal comes from, is 205. Does the periodogram see them all in the full sample? Probably it does, but it cannot define the structure well, due to the small amplitude of the signal. The large number of possible periods tells us that the cubic structure is rather vague so that the full sample can be tiled into cubes in different ways. In the contrary, the ACO8S sample displays a unique regular cubic tiling.

As the final best solutions are close to the supergalactic alignment that we started with, it may seem that the large amount of work done to analyze the full Euler cube was unnecessary. We do not think so; we can be sure that this is the best alignment only after having searched the full parameter space. We also stress that there are no shortcuts, and the full analysis can not be avoided.

Table 2: The best alignments for cubic patterns for various samples. The numeration of the curves for the ACO8S sample is the same as in Fig. 24. All angles are in degrees.
No $\alpha$ $\beta$ $\gamma$ No $\alpha$ $\beta$ $\gamma$

ACO1 ACO8

1 0.0 0.0 0.0 1 10.1 10.1 81.9

2 55.9 87.4 81.0 2 86.2 33.6 82.4

3 72.9 11.0 38.2 3 38.7 22.0 19.1

4 82.0 11.5 27.4 4 66.9 30.3 85.1

5 6.5 81.9 78.1 ACO8S

6 77.0 41.3 85.9 1 6.7 3.9 0.0

7 22.2 11.0 50.1 2 72.0 81.8 69.6

8 68.3 12.1 41.4 3 10.0 14.0 82.3

4 65.0 56.9 80.1

5 55.7 25.1 0.7

6 69.4 65.4 2.7

**Table 2:** The best alignments for cubic patterns for various samples. The numeration of the curves for the ACO8S sample is the same as in Fig. 24. All angles are in degrees.
No	$\alpha$	$\beta$	$\gamma$	No	$\alpha$	$\beta$	$\gamma$
ACO1		ACO8
1	0.0	0.0	0.0	1	10.1	10.1	81.9
2	55.9	87.4	81.0	2	86.2	33.6	82.4
3	72.9	11.0	38.2	3	38.7	22.0	19.1
4	82.0	11.5	27.4	4	66.9	30.3	85.1
5	6.5	81.9	78.1	ACO8S
6	77.0	41.3	85.9	1	6.7	3.9	0.0
7	22.2	11.0	50.1	2	72.0	81.8	69.6
8	68.3	12.1	41.4	3	10.0	14.0	82.3
				4	65.0	56.9	80.1
				5	55.7	25.1	0.7
				6	69.4	65.4	2.7

3.6 Special orientations

Finally, we can check how perfect our cubic symmetry is by computing periodograms for special orientations, like e.g. those aligned along the diagonals of the original cube. In a perfect cubic world there would appear new periods $\sqrt{2}$ times larger, or $\sqrt{3}$ times larger than the basic period, depending on the orientation. In fact, this does not happen in the samples we have studied here. There is almost no trace of a signal for such alignments, and when we choose those as starting points for our period search, the search ends in the same (oblique) alignments summarized in Table 2, or returns to the almost perfect alignment. The two best special orientation periodograms are shown in Fig. 25. Their amplitude is a little larger than for other special orientations, but small compared with the best solution (for ACO8S), that is shown in that Figure for reference. The periodograms describe both the ACO8 and ACO8S samples and their orientation is the same, ( $0^\circ,45^\circ,0^\circ$ ), i.e. they describe cubes rotated around the supergalactic Y-axis by $45^{\circ }$ . A look at Fig. 13 shows that one could really see such a pattern, knowing that it exists.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f30.eps}\end{figure}$

Figure 25: The best periodograms for special orientations of the cubes (the cube axes form $45^{\circ }$ angles with the supergalactic coordinate axes). Our overall best solution for ACO8S (short-dashed line) is shown to compare the amplitudes. The solid line shows the solution for the full ACO8 sample and the dashed line for the ACO8S sample.

3.7 Resolution effects

We used the resolution of 30 points per density kernel throughout this analysis. From the point of view of density calculations, this seems the smallest one can safely choose. On the other hand, for smaller samples this will certainly give a very low spatial resolution (only 7 cubic bins for the 205 clusters of ACO8S). Let us see how the resolution influences the results, and how small one could take the kernel. We compared periodograms with different kernel widths for the ACO8 and ACO8S samples. The results are shown in Fig. 26.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f31.eps}\end{figure}$

Figure 26: Periodograms produced with different kernel sizes (expressed in points per kernel volume) for the ACO8S subsample. The periodograms are labeled with the kernel sizes used.

We chose the best alignments for both samples, started with the standard 30 points per kernel, and then lowered this number down to 5 and 3. We see that the periodograms remain rather smooth even for extremely small kernels (individual densities might be noisy already, but summation smoothes them) and edge effects grow fast. Larger kernels smooth the signal and lower its amplitude, as expected. An interesting trend is that in both cases the periods move towards the magic 130 h^-1 Mpc with smaller smoothing. The choice of a best kernel size is a matter of practice, but we think that our choice of a 30-point kernel was correct since otherwise edge effects could have ruined our search for best alignments. Thus the strategy of using smoother periodograms first for alignment search and refining the periods by a subsequent use of smaller kernels, appears to be good.

3.8 Phase patterns

The regularity periodogram is an interesting curve to study, but it does not tell us exactly what the structure looks like. However, we can find it out easily by plotting the phase cubes. We show two of those in Fig. 27, for the ACO8 and ACO8S samples. We do not show the phase cube for the full sample; as expected, it does not look much different from a Poisson point distribution - the number of points is large and the amplitude of the cubic signal small.

The phase cubes shown correspond to the best alignments, counted as number one in the alignment Table 2. The best periods for these alignments are 120 h^-1 Mpc for ACO8 and 140 h^-1 Mpc for ACO8S. As indicated by high-resolution runs described above (see Fig. 26), we chose a period of 130 h^-1 Mpc for both samples.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{h1676f32.eps}\par\includegraphics[width=8.8cm,clip]{h1676f33.eps}\end{figure}$

Figure 27: Phase cubes for the best alignments and for the period 130 h^-1 Mpc for the ACO8 sample (upper panel) and for the ACO8S subsample (lower panel).

The phase cubes show, firstly, that the cubic regularity really exists; the density distribution in the phase cube is highly inhomogeneous. The signal is mainly due to a rich point cluster plus filamentary features, obtained easiest by folding a lattice with highest concentrations at its vertices. The cubes confirm the picture we get from the amplitude of the signal: for ACO8S with 205 clusters, the extra regularity signal is about one. Assuming that the filling factor of the structure is about 0.3, formula (9) tells us that about 60% of all points could belong to the regular structure. Apart from that, the phase cubes show also that the cubic structure is far from perfect and that one could try to fit other tilings.

3 Regularity of the Abell cluster sample