The histograms of ![]() derived from B and I are presented in Fig. 8. The visible result is that both photometric bands give the
same mean.
derived from B and I are presented in Fig. 8. The visible result is that both photometric bands give the
same mean.
The means
![]() and
and
![]() are obviously not significantly different from each other.
This justifies that the distance moduli in B and I are combined as explained in
the previous section.
Similarly, the
are obviously not significantly different from each other.
This justifies that the distance moduli in B and I are combined as explained in
the previous section.
Similarly, the ![]() will be now the weighted mean of
will be now the weighted mean of ![]() in B and I.
In order to see the influence of Virgo, we plot now
in B and I.
In order to see the influence of Virgo, we plot now ![]() vs.
vs. ![]() .
Three regions are defined (Fig. 9):
.
Three regions are defined (Fig. 9):
Let us study in detail these regions with the target of fitting Peebles' model.
In region III the influence of Virgo is small on individual galaxies because they
are far from the Virgo center but the infall of our Local Group may be not
negligible. If the adopted LG-infall is too large the ![]() for this region
will be too high (and vice versa).
On the contrary, in region Ib (i.e., region I without the central region Ia of
the Virgo center)
one expects
for this region
will be too high (and vice versa).
On the contrary, in region Ib (i.e., region I without the central region Ia of
the Virgo center)
one expects ![]() to diminish when the adopted LG-infall increases. This
is confirmed by Fig. 10 where we calculated the mean
to diminish when the adopted LG-infall increases. This
is confirmed by Fig. 10 where we calculated the mean ![]() in regions Ib and III for different LG-infall velocities. The error bar on
each point is used to define internal uncertainties on
in regions Ib and III for different LG-infall velocities. The error bar on
each point is used to define internal uncertainties on
![]() and
and
![]() .
.
The intersection of the two curves of Fig. 10 gives accurately
both the infall velocity of the LG and ![]() .
We obtain:
.
We obtain:
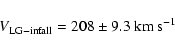 |
(16) |
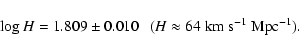 |
(17) |
 |
Figure 8:
Histograms of |
In order to search for possible residual bias, we plotted the mean ![]() of each
calibrator class versus the absolute magnitude of its calibrator, in Band I-band, (Fig. 11).
A tendency to have large
of each
calibrator class versus the absolute magnitude of its calibrator, in Band I-band, (Fig. 11).
A tendency to have large ![]() when the calibrator is
faint might be present for the less luminous calibrator. The slope of this
relation is
when the calibrator is
faint might be present for the less luminous calibrator. The slope of this
relation is
![]() .
This is barely significant at the 0.01 probability level
(to be significant, the Student's t test requires
t0.01>2.57, while we observe
t=0.015/0.006=2.5). If one removes the six less luminous calibrators
(NGC 598, NGC 4496A, NGC 2090, NGC 3319, NGC 3351 and NGC 4639), the
tendency disappears (t=0.4). In this case, the mean log of the Hubble constant
becomes
.
This is barely significant at the 0.01 probability level
(to be significant, the Student's t test requires
t0.01>2.57, while we observe
t=0.015/0.006=2.5). If one removes the six less luminous calibrators
(NGC 598, NGC 4496A, NGC 2090, NGC 3319, NGC 3351 and NGC 4639), the
tendency disappears (t=0.4). In this case, the mean log of the Hubble constant
becomes
![]() (instead of
(instead of
![]() ). Thus, the mean
Hubble constant is not severely affected, but small
). Thus, the mean
Hubble constant is not severely affected, but small
![]() is probably better.
is probably better.
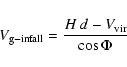 |
(18) |
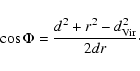 |
(19) |
Now, we can plot
![]() vs. r (Fig. 12) to check directly
Peebles' model (Eq. (1)).
From the previous relation it can be seen that the errors on
x- and y-axis are strongly correlated.
The dominant error comes from d.
The asymptotic velocity infall is zero at large r distances. The location of the LG is
represented by a large open square.
We calculated
vs. r (Fig. 12) to check directly
Peebles' model (Eq. (1)).
From the previous relation it can be seen that the errors on
x- and y-axis are strongly correlated.
The dominant error comes from d.
The asymptotic velocity infall is zero at large r distances. The location of the LG is
represented by a large open square.
We calculated ![]() by minimizing the dispersion on
by minimizing the dispersion on
![]() .
For this
calculation we limited r between 3 Mpc and 30 Mpc in order to avoid the Virgo
center, where there is a very large uncertainty on
.
For this
calculation we limited r between 3 Mpc and 30 Mpc in order to avoid the Virgo
center, where there is a very large uncertainty on
![]() due to the small
value of r.
The best result is obtained for
due to the small
value of r.
The best result is obtained for
![]() .
This result is quite comparable with the value
adopted by Peeblees (
.
This result is quite comparable with the value
adopted by Peeblees (![]() )
but the uncertainty, estimated visually, is large
(about 0.2). The application to the Local Group infall leads to
)
but the uncertainty, estimated visually, is large
(about 0.2). The application to the Local Group infall leads to
![]() .
In order to highlight the tendency, we plot the mean x and y values of individual points
in four x-boxes: (3 to 7) Mpc, (7 to 13) Mpc, (13 to 21) Mpc and (21 to 31) Mpc.
These mean points (open circles) are represented with their observed scatter divided by
the square root of the number of points in each box.
.
In order to highlight the tendency, we plot the mean x and y values of individual points
in four x-boxes: (3 to 7) Mpc, (7 to 13) Mpc, (13 to 21) Mpc and (21 to 31) Mpc.
These mean points (open circles) are represented with their observed scatter divided by
the square root of the number of points in each box.
It is interesting to see in detail which galaxies are exactly in the direction of
the Virgo center. If we consider galaxies with
![]() and
and
![]() only 9 galaxies remain. They are presented in Table 3 following increasing
radial velocities. For each galaxy we give the observed Hubble constant H.
In this table two parameters are independent: the radial velocity and the distance
modulus.
only 9 galaxies remain. They are presented in Table 3 following increasing
radial velocities. For each galaxy we give the observed Hubble constant H.
In this table two parameters are independent: the radial velocity and the distance
modulus.
| PGC | NGC |
|
H | ||
| 0041934 | NGC 4548 | 587 |
|
2.4 | 38 |
| 0042833 | 917 |
|
5.1 | 39 | |
| 0043798 | 1089 |
|
11.7 | 38 | |
| 0042741 | NGC 4639 | 1097 |
|
3.1 | 50 |
| 0043451 | NGC 4725 | 1360 |
|
13.9 | 94 |
| 0041823 | NGC 4536 | 1846 |
|
10.2 | 120 |
| 0041812 | NGC 4535 | 2029 |
|
4.3 | 129 |
| 0041024 | 2069 |
|
4.7 | 114 | |
| 0042069 | 2342 |
|
1.8 | 119 | |
| Mean |
|
||||
| Adopted |
|
The main feature from this table is that the apparent Hubble constants are
sorted according to velocities. This means that the distance does not
intervene very much. The natural interpretation is that all these galaxies
are almost at the same distance (distance of Virgo). The Hubble constant
reflects only the infall velocity.
Large velocities correspond
to galaxies in front of Virgo and falling onto Virgo, away from us. On the contrary,
galaxies with small velocities are beyond Virgo and falling onto it in our direction.
Indeed, the four galaxies with small velocities have a mean distance modulus
of
![]() while the four galaxies with high velocities have a larger
mean distance modulus of
while the four galaxies with high velocities have a larger
mean distance modulus of
![]() .
The difference is significant at
about
.
The difference is significant at
about ![]() .
This confirms clearly the interpretation.
From the table one can conclude that the distance modulus of Virgo is
.
This confirms clearly the interpretation.
From the table one can conclude that the distance modulus of Virgo is
![]() .
However, it is difficult to give a mean radial velocity
because of the strong perturbation of the velocity field. Amazingly, it
is better to measure radial velocities out of the center to obtain a good
mean velocity of a cluster. If one adopts the velocity
of 980 km s-1 (see the discussion in Teerikorpi et al. 1992),
and both the LG-infall velocity and the Hubble constant
found in this paper, the distance modulus of the Virgo cluster is
.
However, it is difficult to give a mean radial velocity
because of the strong perturbation of the velocity field. Amazingly, it
is better to measure radial velocities out of the center to obtain a good
mean velocity of a cluster. If one adopts the velocity
of 980 km s-1 (see the discussion in Teerikorpi et al. 1992),
and both the LG-infall velocity and the Hubble constant
found in this paper, the distance modulus of the Virgo cluster is ![]() .
This gives a coherent system of parameters.
.
This gives a coherent system of parameters.
We can also discuss the region perpendicular to the direction of Virgo
(region II). The weighted mean Hubble constant in this region is
nearly the same as the one found in region III (i.e.,
![]() ).
In the direction of the Fornax cluster one can repeat what we have done
in the direction of Virgo, but the number of galaxies is smaller.
The center of Fornax is assumed to be
).
In the direction of the Fornax cluster one can repeat what we have done
in the direction of Virgo, but the number of galaxies is smaller.
The center of Fornax is assumed to be
![]() and
and
![]() .
In Table 4 we summarize the results. It appear that
galaxies PGC 12390 and PGC 10330 can be considered as backside galaxies
falling onto Fornax
towards us (small radial velocity, large distance, small apparent
Hubble constant). Galaxies PGC 13255 and PGC 13602 are roughly at the
position of Fornax, while PGC13179 and PGC 13059 are in front of Fornax
(large radial velocity, small distance and large apparent Hubble constant).
From the table one can conclude that the distance modulus of Fornax is
.
In Table 4 we summarize the results. It appear that
galaxies PGC 12390 and PGC 10330 can be considered as backside galaxies
falling onto Fornax
towards us (small radial velocity, large distance, small apparent
Hubble constant). Galaxies PGC 13255 and PGC 13602 are roughly at the
position of Fornax, while PGC13179 and PGC 13059 are in front of Fornax
(large radial velocity, small distance and large apparent Hubble constant).
From the table one can conclude that the distance modulus of Fornax is
![]() .
It is not possible to measure how the infall velocity changes with the distance
to the center of Fornax. Nevertheless, if one still adopt
.
It is not possible to measure how the infall velocity changes with the distance
to the center of Fornax. Nevertheless, if one still adopt
![]() one can determine the parameter C for Fornax. Indeed, the observed infall velocity
is roughly 270 km s-1 at a distance of 6 Mpc of the center.
This leads to
one can determine the parameter C for Fornax. Indeed, the observed infall velocity
is roughly 270 km s-1 at a distance of 6 Mpc of the center.
This leads to
![]() .
.
| PGC |
|
H | ||
| 0012390 | 767 |
|
14.5 | 31 |
| 0010330 | 1249 |
|
14.4 | 36 |
| 0013255 | 1279 |
|
11.1 | 53 |
| 0013602 | 1299 |
|
6.0 | 65 |
| 0013179 | 1423 |
|
2.1 | 91 |
| 0013059 | 1670 |
|
3.4 | 91 |
| Mean |
|
Copyright ESO 2002