Determining Local Group membership for nearby galaxies is not a trivial
undertaking. The well-established members of the Local Group have been
used to define a mass-weighted Local Group Standard of Rest,
corresponding to a solar motion of
![]() towards
towards
![]() (Karachentsev & Makarov
1996). The
(Karachentsev & Makarov
1996). The ![]() velocity dispersion of Local
Group galaxies with respect to this reference frame is about
60 km s-1 (Sandage 1986). A plot of heliocentric velocity versus
the cosine of the angular distance between the solar apex and the galaxy
in question, as shown in Fig. 10, has often been used to
assess the likelihood of Local Group membership (e.g. van den Bergh
1994) when direct distance estimates have not been available.
Local Group galaxies tend to lie within about one sigma of the line
defined by the solar motion in the LGSR reference frame. Braun
& Burton (1999) pointed out how the original LDS CHVC sample
followed this relationship, although offset with a significant infall
velocity. The all-sky CHVC sample has been plotted in this way in
Fig. 10. Both the sample size and sky coverage are
significantly enhanced relative to what was available to Braun & Burton. A
systematic trend now becomes apparent in the CHVC kinematics. While the
CHVCs at negative
velocity dispersion of Local
Group galaxies with respect to this reference frame is about
60 km s-1 (Sandage 1986). A plot of heliocentric velocity versus
the cosine of the angular distance between the solar apex and the galaxy
in question, as shown in Fig. 10, has often been used to
assess the likelihood of Local Group membership (e.g. van den Bergh
1994) when direct distance estimates have not been available.
Local Group galaxies tend to lie within about one sigma of the line
defined by the solar motion in the LGSR reference frame. Braun
& Burton (1999) pointed out how the original LDS CHVC sample
followed this relationship, although offset with a significant infall
velocity. The all-sky CHVC sample has been plotted in this way in
Fig. 10. Both the sample size and sky coverage are
significantly enhanced relative to what was available to Braun & Burton. A
systematic trend now becomes apparent in the CHVC kinematics. While the
CHVCs at negative
![]() (predominantly in the southern hemisphere)
tend to lie within the envelope defined by the LGSR solar apex and the
Local Group velocity dispersion, the CHVCs at positive
(predominantly in the southern hemisphere)
tend to lie within the envelope defined by the LGSR solar apex and the
Local Group velocity dispersion, the CHVCs at positive
![]() have a
large negative offset from this envelope. Obscuration by Galactic H I
may well be important in shaping this trend. Only by analyzing realistic
model populations and subjecting them to all of the selection and
sampling effects of the existing surveys can meaningful conclusions be
drawn.
have a
large negative offset from this envelope. Obscuration by Galactic H I
may well be important in shaping this trend. Only by analyzing realistic
model populations and subjecting them to all of the selection and
sampling effects of the existing surveys can meaningful conclusions be
drawn.
![\begin{figure}
\par {\includegraphics[width=16.6cm,clip]{ms2407f23.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg227.gif) |
Figure 23:
Predicted distribution on the sky of detected synthetic clouds
corresponding to the model #9 simulation of a CHVC population in the
Local Group, contrasting LDS and HIPASS sensitivities; the parameters
of the simulation are given in Table 4. The black
dots correspond to objects that exceed the LDS and HIPASS detection
threshold and are not obscured by Galactic H I. The red dots are
predicted additional detections if the HIPASS sensitivity were extended to
the northern hemisphere. The superposed grey-scale image shows, as in
Fig. 5, the observed H I column depths, following from
an integration of observed temperatures over velocities ranging from
|
Recently several simulations have been performed to test the hypothesis that the CHVCs are the remaining building blocks of the Local Group. Putman & Moore (2002) compared the results of the full N-body simulation described by Moore et al. (2001) with various spatial and kinematic properties of the CHVC distribution, as well as with properties of the more general HVC phenomenon, without regard to object size and degree of isolation. Putman & Moore were led to reject the Local Group deployment of CHVCs, for reasons which we debate below. Blitz et al. (1999) performed a restricted three body analysis of the motion of clouds in the Local Group. In their attempt to model the HVC distributions, Blitz et al. modeled the dynamics of dark matter halos in the Local Group and found support for the Local Group hypothesis when compared qualitatively with the deployment of a sample of anomalous-velocity H I containing most HVCs, but excluding the large complexes (including the Magellanic Stream) for which plausible or measured distance constraints are available. Assuming that 98% of the Local Group mass is confined to the Milky Way and M 31 and their satellites, Blitz et al. described the dynamics of the Local Group in a straightforward manner. Driven by their mutual gravity and the tidal field of the neighboring galaxies, the Milky Way and M 31 approach each other on a nearly radial orbit. The motion of the dark matter halos which fill the Local Group was determined by the gravitational attraction of the Milky Way and M 31, and the tidal field of the neighboring galaxies. All halos which ever got closer than a comoving distance of 100 kpc from the Milky Way or M 31 center were removed from the sample. Blitz et al. describe how their simulations account for several aspects of the HVC observations. We follow here the modeling approach of Blitz et al., but judge the results of our simulations against the properties of the CHVC sample, viewing the simulated data as if it were observed with the LDS and HIPASS surveys.
We use a test particle approach similar to that used by Blitz et al. (1999) to derive the kinematic history of particles as a
function of their current position within the Local Group, but combine
this with an assumed functional form (rather than simply a uniform
initial space density) to describe the number density distribution of
the test particles. The density function contains a free parameter
which sets the degree of concentration of the clouds around the Milky
Way and M 31. By determining a best fit of the models we are able to
constrain the values of this concentration parameter, and thereby
constrain the distance to the CHVCs. The fits depend upon the derived
velocity field and the H I properties of the clouds.
![\begin{figure}
{\includegraphics[width=11.3cm,clip]{ms2407f24.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg228.gif) |
Figure 24:
Demonstration of the quality of the fits of the
Galactic Halo models discussed in Sect. 5. The
upper panels show the column-density fits; the lower panels show the
size fits. The panels on the left represent one of the
better fits, characterized by
|
The density fields which we use are a sum of two Gaussian distributions,
centered on the Galaxy and M 31, respectively. As a free parameter we
use the radial dispersion of these distributions. This free parameter
has the same value for both the concentration around the Galaxy and that
around M 31. The ratio of the central densities of the distributions at
M 31 and the Galaxy must also be specified. We set this ratio
equal to the mass ratio of the two galaxies. The Gaussian dispersions
which are used in the models range from 100 kpc to 2 Mpc;
i.e. the distributions range from very tightly concentrated around
the galaxies to an almost homogeneous filling of the Local Group.
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f25.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg232.gif) |
Figure 25:
Summary of the simulated spatial and kinematic properties of
the CHVC ensemble, for one of the better fits of the empirical Galactic
Halo model described in Sect. 5. The panels give the
properties of the simulation in the same way as the panels in
Fig. 9 describe the observed data. This Galactic
Halo simulation is determined by the following parameters:
|
The CHVC kinematics are simulated by tracking the motions of small test
particles within the gravitational field of the Milky Way, the M 31
system, and the nearby galaxies. Both the description of the tidal
field that is produced by the nearby galaxies, and the properties of
the Galaxy-M 31 orbit, are taken from the analysis of Raychaudhury
& Lynden-Bell (1989), who studied the influence of
the tidal field on the motion of the Galaxy and M 31, deriving
the dipole tidal field from a catalog of galaxies compiled by
Kraan-Korteweg (1986). The motions of the Galaxy and
M 31 are determined in a simulation. In this simulation M 31
and the Galaxy are released a short time after the Big Bang. The
initial conditions are tuned in such a way that the relative radial
velocity and position correspond with the values currently measured.
![\begin{figure}
\par {\includegraphics[width=17.3cm,clip]{ms2407f26.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg235.gif) |
Figure 26:
Summary of the simulated spatial and kinematic properties of
the CHVC ensemble, for one of the better fits of the empirical Galactic
Halo model described in Sect. 5. The panels give the
properties of the simulation in the same way as the panels in
Fig. 9 describe the observed data. This Halo
simulation is determined by the following parameters:
|
We track not only the motions of M 31 and the Galaxy, but also the motions of a million test particles. The test particles are, together with M 31 and the Milky Way, released a short time after the Big Bang with a velocity equal to that of the Hubble flow. Initially, the test particles homogenously fill a sphere with a comoving radius of 2.5 Mpc. Their motions are completely governed by the gravitational field of M 31 and the Milky Way and by the tidal field of the nearby galaxies. The result of the simulation at the present age of the Universe is used to define the kinematic history as a function of current 3-D position within the Local Group for our simulated CHVC populations. For every 3-D position where an object is to be placed by our assumed density distribution, we simply assign the kinematic history from the test particle in the kinematic simulation which ended nearest to that 3-D position. The most important aspects of the kinematic history are merely the final space velocity vector as well as the parameters of the closest approach of the test particle to M 31 and the Milky Way, where the effects of ram pressure and tidal stripping will be assessed.
The parameters which determine the outcome of the simulation are the
Hubble constant, H, the average density of the Universe, ![]() ,
the total mass of the Local Group,
,
the total mass of the Local Group,
![]() ,
(=
,
(=
![]() +
+
![]() ), and the mass-to-light ratio of the nearby galaxies, which make
up the tidal field. The Hubble constant and the average density of the
Universe not only set the age of the Universe, but also the initial
velocities of the test particles. Further evolution is independent of
these parameters. The evolution is set by the values of the tidal
field and the masses of M 31 and the Galaxy. Values for all these
parameters were taken from Raychaudhury and Lynden-Bell
(1989), namely:
), and the mass-to-light ratio of the nearby galaxies, which make
up the tidal field. The Hubble constant and the average density of the
Universe not only set the age of the Universe, but also the initial
velocities of the test particles. Further evolution is independent of
these parameters. The evolution is set by the values of the tidal
field and the masses of M 31 and the Galaxy. Values for all these
parameters were taken from Raychaudhury and Lynden-Bell
(1989), namely:
![]() ,
,
![]() ,
a mass-to-light ratio of 60,
,
a mass-to-light ratio of 60,
![]() ,
and
,
and
![]() .
Whereas the mutual
gravitational attraction between the Milky Way and M 31 is described
by a point-mass potential, the gravitational attraction of these
galaxies on the test particles is described by an isochrone potential
of the form
.
Whereas the mutual
gravitational attraction between the Milky Way and M 31 is described
by a point-mass potential, the gravitational attraction of these
galaxies on the test particles is described by an isochrone potential
of the form
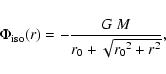 |
(4) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{ms2407f27.ps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg248.gif) |
Figure 27: Histogram of object distances for one of the best-fitting Local Group models. The detected objects in model #9 of Table 4 are plotted in the histogram. A broad peak in the distribution extends from about 200 to 450 kpc, with outliers as far as 1 Mpc. The filled circles along the top of the figure are the distance estimates for individual CHVCs of Braun & Burton (2000) and Burton et al. (2001), based on several different considerations. While few in number, they appear consistent with this distribution. |
![\begin{figure}
\includegraphics[width=7.6cm,clip]{ms2407f28.ps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg250.gif) |
Figure 28:
Comparison of a model Local Group CHVC population with the
population of Local Group galaxies. The distribution of H I masses of
one of our best-fitting Local Group models, model #9 of
Table 4, is plotted as a thin-line histogram after
accounting for ram-pressure and tidal stripping and as a thick line
after also accounting for Galactic obscuration and the finite
sensitivities of the LDS and HIPASS observations. The Local Group
galaxies (excluding M 31 and the Galaxy) tabulated by Mateo
(1998) are plotted as the hatched histogram after summing the
H I mass with the stellar mass assuming
|
Before we can simulate the way in which a Local Group population of
clouds would be observed by a HIPASS- or LDS-like survey, we have to
set the H I properties of the test clouds. To do so, we assume that
the H I clouds are isothermal gas spheres, with each such cloud located
inside a dark-matter halo. Given the temperature of the gas and the
potential in which it resides, the density profile follows from the
relation
The description of the gravitational potential of the dark matter halo
follows that of Burkert (1995), who was able to fit a
universal function to the rotation curves of four different
dwarf galaxies. The shape of the function is completely set by the
amount of dark matter in the core, M0. The potential, which is
derived from the rotation curve, has the form
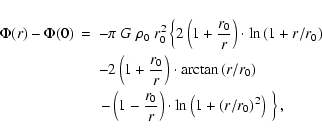
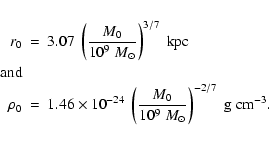
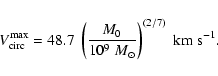 |
(7) |
Although we could use Eq. (5) directly to determine the
predicted 21-cm images of a CHVC given an H I mass, we instead chose
to approximate the corresponding column-density distribution by a
Gaussian, in order to enable faster evaluation of the simulation. Two
parameters specify the Gaussian, namely the central density, n0, and
the FWHM, derived as follows. The volume-density distribution given
by Eq. (5), can be closely approximated with an
exponential form with a matched scale-length, ![]() ,
defined by
,
defined by
![]() .
The column density distribution can then be
expressed in an analytic form, containing a modified Bessel function of
order 1 (e.g. Burton et al. 2001). This analytic
representation of the column-density distribution is then approximated
by a Gaussian of the same halfwidth from,
.
The column density distribution can then be
expressed in an analytic form, containing a modified Bessel function of
order 1 (e.g. Burton et al. 2001). This analytic
representation of the column-density distribution is then approximated
by a Gaussian of the same halfwidth from,
![]() .
Knowing
the mass of the H I gas cloud and its FWHM, the central density of the
Gaussian can be determined.
.
Knowing
the mass of the H I gas cloud and its FWHM, the central density of the
Gaussian can be determined.
To get the amount of H I mass in the cloud, we adopt the relations
between the dark-matter mass and baryonic mass for galaxies. For
normal, massive galaxies there is approximately ten times as much dark
matter as there is baryonic matter. Chiu et al. (2001) show
that this ratio depends on the total mass. Whereas the mass spectrum
of the dark-matter halos in their simulation has the form
![]() ,
the baryonic mass spectrum has the
form
,
the baryonic mass spectrum has the
form
![]() .
The difference in
slope is due to the ionizing extragalactic radiation field. The lowest
mass halos are simply unable to retain their ionized baryonic
envelopes, which have a kinetic temperature of 104 K. The slopes of
both the baryonic and the dark-matter distributions completely determine
the mass dependency of the ratio between dark matter and baryonic
matter. Furthermore, given the fact that the ratio equals 10 for
objects with a baryonic mass of
.
The difference in
slope is due to the ionizing extragalactic radiation field. The lowest
mass halos are simply unable to retain their ionized baryonic
envelopes, which have a kinetic temperature of 104 K. The slopes of
both the baryonic and the dark-matter distributions completely determine
the mass dependency of the ratio between dark matter and baryonic
matter. Furthermore, given the fact that the ratio equals 10 for
objects with a baryonic mass of
![]() ,
the ratio is set
for all masses. Although the simulation of Chiu et al. gives a value
of -1.6 for the baryonic mass spectrum slope, we explore a range of
values for the H I mass spectrum. The most appropriate value is then
obtained by fitting the models to the observations.
,
the ratio is set
for all masses. Although the simulation of Chiu et al. gives a value
of -1.6 for the baryonic mass spectrum slope, we explore a range of
values for the H I mass spectrum. The most appropriate value is then
obtained by fitting the models to the observations.
For the sake of simplicity, we assume that the baryonic mass of each simulated cloud is entirely in the form of H I. In fact, a significant mass fraction will be in the form of ionized gas. It is likely that the mass fraction of ionized gas will increase toward lower masses such that below some limiting mass the objects would be fully ionized. A realistic treatment of the ionized mass fraction was deemed beyond the scope of this study. However, we do comment further on the implications of this simplifying assumption where appropriate.
The definitions of the velocity and density fields of the test objects in the Local Group, together with their H I properties, resulted in simulated CHVC populations which could be sampled with the observational parameters of an LDS- or HIPASS-like survey. The free parameters, defined above, were allowed to take the following values:
Figure 12 shows the basic cloud properties as a
functions of H I mass. As indicated above, the dark-matter fraction as
function of mass is determined by ![]() ,
the slope of the H I mass
spectrum, so three curves are shown in each panel, corresponding to
,
the slope of the H I mass
spectrum, so three curves are shown in each panel, corresponding to
![]() ,
-1.6, and -2.0, respectively. The typical object
size and internal velocity dispersion increases only slowly with H I
mass, from about 1.5 to 4 kpc, and 10 to 20 km s-1, respectively, between
,
-1.6, and -2.0, respectively. The typical object
size and internal velocity dispersion increases only slowly with H I
mass, from about 1.5 to 4 kpc, and 10 to 20 km s-1, respectively, between
![]() and
and
![]() .
The central H I volume
density varies much more dramatically with H I mass, as does the peak
column density. Note that the peak column densities of simulated clouds
only exceed
.
The central H I volume
density varies much more dramatically with H I mass, as does the peak
column density. Note that the peak column densities of simulated clouds
only exceed
![]() cm-2 for
cm-2 for
![]() and
and ![]() in the range -1.6--2.0. It
is critical that peak column densities of this order are achieved in
long-lived objects, since this is required for self-shielding from the
extragalactic ionizing radiation field (e.g. Maloney 1993;
Corbelli & Salpeter 1993).
in the range -1.6--2.0. It
is critical that peak column densities of this order are achieved in
long-lived objects, since this is required for self-shielding from the
extragalactic ionizing radiation field (e.g. Maloney 1993;
Corbelli & Salpeter 1993).
In order to compare the simulation results with the observational data
in the most effective way, and thereby constrain the model parameters,
we created a single CHVC catalog from the HIPASS and LDS ones.
Thirty-eight CHVCs at
![]() were extracted from the de Heij
et al. (2002) LDS catalog, and 179 at
were extracted from the de Heij
et al. (2002) LDS catalog, and 179 at
![]() from the Putman et al. (2002) HIPASS one. A large
concentration of faint sources (Group 1 noted above) with an
exceptionally high velocity dispersion is detected toward the Galactic
south pole. Because this overdensity may well be related to the nearby
Sculptor group of galaxies (see Putman et al. 2002), the 53
CHVCs at
from the Putman et al. (2002) HIPASS one. A large
concentration of faint sources (Group 1 noted above) with an
exceptionally high velocity dispersion is detected toward the Galactic
south pole. Because this overdensity may well be related to the nearby
Sculptor group of galaxies (see Putman et al. 2002), the 53
CHVCs at
![]() were excluded from comparison with the
simulations.
were excluded from comparison with the
simulations.
A simulation was run for each set of model parameters. We
chose a position for each object, in agreement with the spatial density
distribution of the ensemble, but otherwise randomly. The velocity is
given by the velocity field described above. The H I mass of the test
cloud is randomly set in agreement with the given power-law mass
distribution between the specified upper mass limit and a lower mass
limit described below. The physical size and linewidth of each object
follow from the choice of
![]() .
Once all these parameters were set, we determined the observed
peak column density and angular size. Objects in the northern
hemisphere were convolved with a beam appropriate to the LDS, while
those at
.
Once all these parameters were set, we determined the observed
peak column density and angular size. Objects in the northern
hemisphere were convolved with a beam appropriate to the LDS, while
those at
![]() were convolved with the HIPASS beam.
Simulated objects were considered detected if the peak brightness
temperature exceeded the detection threshold of the relevant survey,
i.e. the LDS for objects at
were convolved with the HIPASS beam.
Simulated objects were considered detected if the peak brightness
temperature exceeded the detection threshold of the relevant survey,
i.e. the LDS for objects at
![]() ,
and HIPASS otherwise.
Furthermore, in order for a test object to be retained as detected its
deviation velocity was required to exceed
,
and HIPASS otherwise.
Furthermore, in order for a test object to be retained as detected its
deviation velocity was required to exceed
![]() in the LSR
frame, and its Galactic latitude to be above
in the LSR
frame, and its Galactic latitude to be above
![]() (for
consistency with the exclusion of Group 1 from our CHVC sample noted
above). In addition, as we describe below, each simulated cloud should
be stable against both tidal disruption and ram-pressure stripping by
the Milky Way and M 31. We continued simulating additional objects
following this prescription until the number of detected model clouds
was equal to the number of CHVCs in our observed all-sky sample.
(for
consistency with the exclusion of Group 1 from our CHVC sample noted
above). In addition, as we describe below, each simulated cloud should
be stable against both tidal disruption and ram-pressure stripping by
the Milky Way and M 31. We continued simulating additional objects
following this prescription until the number of detected model clouds
was equal to the number of CHVCs in our observed all-sky sample.
![\begin{figure}
\includegraphics[width=11cm,clip]{ms2407f29.ps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg284.gif) |
Figure 29:
External appearance of a model Local Group CHVC population.
The spatial distribution of one of our best-fitting Local Group models,
namely model #9 of Table 4, is shown projected onto a
plane as in Fig. 20. The grey
dots correspond to objects which have been disrupted by ram-pressure or
tidal stripping during a close passage. The red and black dots
correspond to are objects which should survive these processes, with the
color of the dot distinquishing objects by H I mass. The red dots
indicate clouds more massive than
|
Before carrying out each simulation with a power-law distribution of H I masses we began by determining an effective lower H I mass limit, M0, to the objects that should be considered. This was necessary to avoid devoting most of the calculation effort to objects too faint to be detected in any case. As a first guess we took M0=0.5 M1. A sub-sample of twenty objects in the mass range M0-M1 was simulated which were deemed stable to both disruption and stripping and were detectable with the relevant survey parameters. Generating twenty detectable objects typically required evaluating of order 500 test objects. Given the total number of test objects needed to generate this observable sub-sample and the slope of the H I mass distribution function, it is possible to extrapolate the number of required test objects in other intervals of H I mass belonging to this same distribution. The predicted number of test objects in the interval 0.67 M0 to M0 was simulated. If at least one of these was deemed detectable, then the lower H I mass limit was replaced with 0.67 M0 and the procedure outlined above was repeated. This process continued until no detectable object was found in the mass interval 0.67 M0 to M0. Tests carried out with better number statistics, involving a sub-sample size of 180 objects and requiring a minimum of nine detections in the lowest mass interval, demonstrated that this procedure was robust.
Figure 13 shows the distance out to which
simulated CHVCs of a given H I mass can be detected with the HIPASS
survey. Both the H I linewidth and spatial FWHM are dependent on the
dark-matter fraction, as illustrated in Fig. 12, so
separate curves are shown for
![]() ,
-1.6, and
-2.0. A limiting case is provided by
,
-1.6, and
-2.0. A limiting case is provided by
![]() which is
extremely dark-matter dominated for low H I mass. In this case the
objects are so spatially extended (about 5 kpc FWHM) and have such a
high linewidth (about 60 km s-1 FWHM) that they fall below the HIPASS
detection threshold for log(
which is
extremely dark-matter dominated for low H I mass. In this case the
objects are so spatially extended (about 5 kpc FWHM) and have such a
high linewidth (about 60 km s-1 FWHM) that they fall below the HIPASS
detection threshold for log(
![]() .
More plausible
linewidths and spatial FWHM follow for
.
More plausible
linewidths and spatial FWHM follow for
![]() and
-2.0. Such objects are sufficiently concentrated that they can still
be detected, even when highly resolved in the HIPASS data.
and
-2.0. Such objects are sufficiently concentrated that they can still
be detected, even when highly resolved in the HIPASS data.
The clouds are regarded stable against ram-pressure stripping if the
gas pressure at the center of the cloud exceeds the ram pressure,
![]() ,
for a cloud moving with
velocity V through a gaseous halo with density
,
for a cloud moving with
velocity V through a gaseous halo with density
![]() .
Because both the gaseous halo density and the cloud velocity are the
highest if the distance of the cloud to the galaxy is the smallest, the
stability against ram-pressure stripping was evaluated at closest
approach. We therefore kept track of the closest approach of each
test-particle to the Galaxy and to M 31, while simulating the velocity
field of the Local Group. We used a density profile for the Galactic
halo which is an adaptation of the model of Pietz et al.
(1998), derived to explain the diffuse soft X-ray emission as
observed by ROSAT. Whereas their model is flattened towards the
Galactic plane, we simply use a spherical density distribution, in
which the radial profile is equal to the Galactic plane density profile
of Pietz et al. The density at a distance r from the Galactic center
is given by
.
Because both the gaseous halo density and the cloud velocity are the
highest if the distance of the cloud to the galaxy is the smallest, the
stability against ram-pressure stripping was evaluated at closest
approach. We therefore kept track of the closest approach of each
test-particle to the Galaxy and to M 31, while simulating the velocity
field of the Local Group. We used a density profile for the Galactic
halo which is an adaptation of the model of Pietz et al.
(1998), derived to explain the diffuse soft X-ray emission as
observed by ROSAT. Whereas their model is flattened towards the
Galactic plane, we simply use a spherical density distribution, in
which the radial profile is equal to the Galactic plane density profile
of Pietz et al. The density at a distance r from the Galactic center
is given by
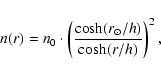 |
(8) |
A cloud will be tidally disrupted if the gravitational tidal field of
either the Galaxy or M 31 exceeds the self-gravity of the cloud.
We consider a cloud stable if
Before searching for a global best fit, we determined the range of
parameter values over which at least a moderately good representation
of the observed data was possible with the simulated data. To quantify
the degree of agreement between the simulated size-, column-density
and velocity-FWHM distributions with the observations, we used a
![]() -test taken from Sect. 14.3 of Numerical Recipes (Press et al. 1993). The size-, column-density, and velocity-FWHM
distributions of a simulation were considered reasonable if
-test taken from Sect. 14.3 of Numerical Recipes (Press et al. 1993). The size-, column-density, and velocity-FWHM
distributions of a simulation were considered reasonable if
![]() ,
,
![]() ,
and
,
and
![]() .
The incorporation of the spatial and kinematic information
was done by comparing the modeled (l,b),
.
The incorporation of the spatial and kinematic information
was done by comparing the modeled (l,b),
![]() ,
and
,
and
![]() distributions with those observed. We used the
two-dimensional K-S test described in Sect. 14.7 of Numerical
Recipes to make this comparison. The fits were considered acceptable if
distributions with those observed. We used the
two-dimensional K-S test described in Sect. 14.7 of Numerical
Recipes to make this comparison. The fits were considered acceptable if
![]() ,
,
![]() ,
and
,
and
![]() where all less than 0.3.
where all less than 0.3.
Table 3 shows which part of the parameter space
produces moderately good fits. The best fits have a Gaussian dispersion
between 150 and
![]() ,
an upper H I mass cut-off between
106.5 and
,
an upper H I mass cut-off between
106.5 and
![]() and a slope of the H I mass
distribution of -1.7 to -1.9.
and a slope of the H I mass
distribution of -1.7 to -1.9.
| M1=
|
|
|
|
|
|
|
|
|
|
|||||||
| -1.4 | |||||||
| -1.6 | |||||||
| -1.7 |
|
150
|
150
|
150
|
|||
| -1.8 |
|
|
|
||||
| -1.9 |
|
|
|||||
| -2.0 |
Each simulation contains a relatively small number of detectable
objects, namely the same number of objects as in our all-sky CHVC
catalog. Therefore the ![]() values are prone to shot-noise. By
performing a larger number of simulations for a specific combination of
free parameters, we are able to determine a more representative value
of
values are prone to shot-noise. By
performing a larger number of simulations for a specific combination of
free parameters, we are able to determine a more representative value
of ![]() for each model. The most promising combinations of
parameter values, i.e. the entries in Table 3, were
repeated 35 times to reduce the shot-noise, and the average results and
their dispersions are shown in Table 4. The range of
resulting fit quality due purely to this shot-noise is illustrated in
Fig. 16, which shows model data with the highest and
lowest
for each model. The most promising combinations of
parameter values, i.e. the entries in Table 3, were
repeated 35 times to reduce the shot-noise, and the average results and
their dispersions are shown in Table 4. The range of
resulting fit quality due purely to this shot-noise is illustrated in
Fig. 16, which shows model data with the highest and
lowest ![]() values from a sequence of 35 simulations.
values from a sequence of 35 simulations.
The best overall fits are fairly well-constrained to lie between
![]() and
and
![]() ,
with an upper H I mass cut-off of about
107 to
,
with an upper H I mass cut-off of about
107 to
![]() and a slope of the H I mass
distribution of -1.7 to -1.8. Comparison with
Fig. 12 suggests that populations of these types have
sufficiently high peak H I column densities that they can provide
self-shielding to the extragalactic ionizing radiation field for
and a slope of the H I mass
distribution of -1.7 to -1.8. Comparison with
Fig. 12 suggests that populations of these types have
sufficiently high peak H I column densities that they can provide
self-shielding to the extragalactic ionizing radiation field for
![]() .
The results of simulations #9
and #3 from Table 4 are shown in
Figs. 17 and 18, respectively. A
single instance of each simulation has been used in the subsequent
figures that had
.
The results of simulations #9
and #3 from Table 4 are shown in
Figs. 17 and 18, respectively. A
single instance of each simulation has been used in the subsequent
figures that had ![]() values consistent with the ensemble average.
values consistent with the ensemble average.
| Model |
|
M1 |
|
|
|
|
|
|
|
| # | (kpc) |
|
|||||||
| 1 | 150 | 106.5 | -1.7 | 2.0 |
1.9 |
4.0 |
0.29 |
0.25 |
0.29 |
| 2 | 150 | 107.0 | -1.7 | 2.2 |
2.3 |
3.5 |
0.27 |
0.23 |
0.28 |
| 3 | 150 | 107.5 | -1.7 | 2.6 |
2.7 |
3.9 |
0.25 |
0.21 |
0.25 |
| 4 | 150 | 108.0 | -1.7 | 3.0 |
3.0 |
3.9 |
0.24 |
0.21 |
0.24 |
| 5 | 150 | 107.0 | -1.8 | 2.0 |
2.4 |
4.5 |
0.27 |
0.23 |
0.28 |
| 6 | 150 | 107.5 | -1.8 | 2.4 |
2.6 |
4.1 |
0.25 |
0.21 |
0.24 |
| 7 | 150 | 108.0 | -1.8 | 2.7 |
2.7 |
4.0 |
0.24 |
0.21 |
0.24 |
| 8 | 200 | 106.5 | -1.7 | 2.4 |
2.9 |
4.9 |
0.29 |
0.28 |
0.30 |
| 9 | 200 | 107.0 | -1.7 | 2.3 |
2.9 |
4.1 |
0.28 |
0.24 |
0.29 |
| 10 | 200 | 107.5 | -1.7 | 2.9 |
3.0 |
4.8 |
0.26 |
0.22 |
0.26 |
| 11 | 200 | 108.0 | -1.7 | 3.0 |
3.1 |
4.9 |
0.26 |
0.22 |
0.25 |
| 12 | 200 | 107.0 | -1.8 | 2.2 |
3.6 |
4.2 |
0.28 |
0.24 |
0.29 |
| 13 | 200 | 107.5 | -1.8 | 2.5 |
3.7 |
3.8 |
0.27 |
0.22 |
0.27 |
| 14 | 200 | 108.0 | -1.8 | 2.7 |
3.7 |
3.6 |
0.26 |
0.22 |
0.26 |
| 15 | 200 | 107.5 | -1.9 | 2.3 |
4.0 |
4.8 |
0.26 |
0.22 |
0.27 |
| 16 | 200 | 108.0 | -1.9 | 2.4 |
4.0 |
4.3 |
0.26 |
0.22 |
0.26 |
| 17 | 250 | 107.0 | -1.7 | 2.3 |
4.3 |
4.8 |
0.28 |
0.24 |
0.29 |
| 18 | 250 | 107.0 | -1.8 | 2.2 |
5.2 |
4.1 |
0.26 |
0.23 |
0.27 |
| 19 | 250 | 107.5 | -1.8 | 2.5 |
5.1 |
3.8 |
0.25 |
0.22 |
0.26 |
| 20 | 250 | 108.0 | -1.8 | 2.7 |
5.3 |
3.6 |
0.25 |
0.22 |
0.25 |
| 21 | 250 | 107.5 | -1.9 | 2.3 |
5.6 |
4.8 |
0.26 |
0.22 |
0.26 |
| 22 | 250 | 108.0 | -1.9 | 2.5 |
5.6 |
4.3 |
0.25 |
0.22 |
0.25 |
Both of these Local Group simulations succeed reasonably well in reproducing the observed kinematic and population characteristics of the CHVC sample as summarized in Fig. 9. The CHVC concentrations, named Groups 2, 3, and 4 above, while not reproduced in detail, have counterparts in the simulations which arise from the combination of Gaussian density distributions centered on the Galaxy and M 31, together with the Local Group velocity field, population decimation by disruption effects, and the foreground H I obscuration. A notable success of these simulations is their good reproduction of the smoothed velocity field, including both the numerical values and the location of minima and maxima.
One aspect of the observed CHVC distributions which can not be reproduced accurately by our simulations is the distribution of observed linewidth. The model objects are assumed to contain only the warm component of H I with a minimum linewidth corresponding to a 8000 K gas. The profiles are then further broadened by the contribution of rotation as indicated in Eq. (6). The actual objects are known to have cool core components (e.g. Braun & Burton 2001; Burton et al. 2001) which can contribute a significant fraction of the H I mass and consequently lead to narrower observed line profiles. This shortcoming of the model distributions is illustrated in the central panel of Fig. 16. The narrow-linewidth tail of the observed distributions can never be reproduced by the models. The best-fitting models can only succeed in reproducing the median value and high-velocity tail of the distribution.
In order to better isolate the effect of foreground obscuration from the intrinsic distribution properties of the simulation itself we show the unobscured version of model #9 in Fig. 19. Comparison of Figs. 17 and 19 illustrates how the foreground obscuration from the H I Zone of Avoidance modifies the distribution of object density. The location of apparent object concentrations are shifted and density contrasts are enhanced. The comparison also reveals that the large gradient in the smoothed GSR velocity field is an intrinsic property of the Local Group model and not simply an artifact of the Galactic obscuration. Substantial negative velocities (<-100 km s-1) are predicted in the direction of M 31 (which effectively defines the Local Group barycenter), while slightly positive velocities are predicted in the anti-barycenter direction, just as observed.
A better appreciation of the physical appearance of these Local Group models is provided in Fig. 20, where two perpendicular projections of the model #9 population are displayed. The (x,y)plane in the figure is the extended Galactic plane, with the Galaxy centered at (x,y)=(0,0) with the positive z axis corresponding to positive b. The intrinsic distribution of objects is an elongated cloud encompassing both the Galaxy and M 31, which is dominated in number by the M 31 concentration. The objects that have at some point in their history approached so closely to either of these galaxies that their H I would not survive the ram-pressure or tidal stripping are indicated by the filled black circles. Cloud disruption appears to have been substantially more important in the M 31 concentration than for the Galaxy. The objects that are too faint to have been detected by the LDS or HIPASS observations, depending on declination, are indicated by grey circles. The bulk of the M 31 sub-concentration is not detected in our CHVC sample for two reasons: (1) these objects have a larger average distance than the objects in the Galactic sub-concentration, and (2) the M 31 sub-concentration is located primarily in the northern celestial hemisphere, where the lower LDS sensitivity compromises detection. We will return to this point below.
Those objects which are obscured by the H I distribution of the Galaxy
are indicated in Fig. 20 by open red circles. Somewhat
counter-intuitively, the consequences of obscuration are not
concentrated toward the Galactic plane, but instead occur in the plane
perpendicular to the LGSR solar apex direction
![]() .
This can be understood by referring back
to our discussion in Sect. 2.2.1 and the illustration in
Fig. 1. Obscuration from the position- and
velocity-dependent H I Zone of Avoidance is most dramatic when the
kinematic properties of a population result in overlap with
.
This can be understood by referring back
to our discussion in Sect. 2.2.1 and the illustration in
Fig. 1. Obscuration from the position- and
velocity-dependent H I Zone of Avoidance is most dramatic when the
kinematic properties of a population result in overlap with
![]() = 0 km s-1, since this can occur over a large solid angle, while the Galactic
plane is relatively thin.
= 0 km s-1, since this can occur over a large solid angle, while the Galactic
plane is relatively thin.
The various processes which influence the observed distributions are
further quantified in Table 5. Matching the detected
sample size of 163 CHVCs above
![]() ,
required the simulation
of some 6300 objects in the case of models #9 and #3. About three
quarters of the simulated populations were classified as disrupted due
to ram-pressure or tidal stripping; while 80% of the remaining objects
were deemed too faint to detect with the LDS (in the north) or
HIPASS (in the south). Obscuration by Galactic H I eliminated about
one half of the otherwise detectable objects. The total H I masses
involved in these two model populations were
,
required the simulation
of some 6300 objects in the case of models #9 and #3. About three
quarters of the simulated populations were classified as disrupted due
to ram-pressure or tidal stripping; while 80% of the remaining objects
were deemed too faint to detect with the LDS (in the north) or
HIPASS (in the south). Obscuration by Galactic H I eliminated about
one half of the otherwise detectable objects. The total H I masses
involved in these two model populations were
![]()
![]() and
and
![]()
![]() ,
respectively. In both cases, about 75%
of this mass had already been consumed by M 31 and the Galaxy via
cloud disruption, leaving only 25% still in circulation, although
distributed over some 1200 low-mass objects.
,
respectively. In both cases, about 75%
of this mass had already been consumed by M 31 and the Galaxy via
cloud disruption, leaving only 25% still in circulation, although
distributed over some 1200 low-mass objects.
| Fate of input CHVCs | model #9 | model #3 | ||
| number |
|
number |
|
|
| of CHVCs | (
|
of CHVCs | (
|
|
| Total number | 6281 | 43 | 6310 | 64 |
| Disrupted by ram or tide | 4759 | 31 | 5178 | 50 |
| Too faint to be detected | 1220 | 6.5 | 831 | 4.4 |
| Detectable if not obscured | 302 | 5.4 | 301 | 10 |
| Unobscured by H I ZoA | 173 | 3.3 | 172 | 6.5 |
| Unobscured, not at SGP | 163 | 3.2 | 163 | 6.4 |
The crucial role of survey sensitivity in determining what is seen of
such Local Group cloud populations is also illustrated in
Figs. 21 and 22. The red symbols in
these figures indicate objects detectable with the relevant LDS or
HIPASS sensitivities, while the black symbols indicate those that
remain undetected due to either limited sensitivity or obscuration. If these
models describe the actual distribution of objects, then the prediction
is that future deeper surveys will detect large numbers of objects at
high negative LSR velocities in the general vicinity (about
![]() )
of M 31. To make this prediction more specific, we
have imagined the sensitivity afforded by the current HIPASS survey in
the south extended to the entire northern hemisphere.
Figure 23 illustrates the prediction. A high
concentration of about 250 faint newly detected CHVCs is predicted in
the Local Group barycenter direction once HIPASS sensitivity is
available.
)
of M 31. To make this prediction more specific, we
have imagined the sensitivity afforded by the current HIPASS survey in
the south extended to the entire northern hemisphere.
Figure 23 illustrates the prediction. A high
concentration of about 250 faint newly detected CHVCs is predicted in
the Local Group barycenter direction once HIPASS sensitivity is
available.
Copyright ESO 2002