

Up: An all-sky study of
Subsections
3 All-sky spatial, kinematic, and column density properties of
the CHVC ensemble
We show in this section the basic observational data for the all-sky
properties of the CHVCs; specifically, the deployment in position and
velocity as well as the perceived size and H I column density
distributions. These basic properties constitute the observables
against which the simulations described in the following sections are
tested.
![\begin{figure}
{\includegraphics[width=12cm,clip]{ms2407f11.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg190.gif) |
Figure 11:
Average velocity field in the Local Group entering the
simulations described in Sect. 4. The velocity at each
grid point is given by the average velocity of all the test particles
located in a box centered on the grid point and with a width of 10 kpc.
Squares are drawn if the velocity dispersion of the ensemble of
particles exceeds
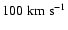 .
The length of the thick line
in the upper left corresponds to a velocity of .
The length of the thick line
in the upper left corresponds to a velocity of
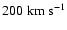 .
The image corresponds to a simulation with a Local Group mass of .
The image corresponds to a simulation with a Local Group mass of
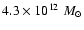 .
The Milky Way and M 31 are located at .
The Milky Way and M 31 are located at
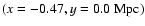 and
and
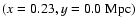 ,
respectively. The contours show the relative
density levels of a combination of two Gaussian distributions with
200 kpc dispersion, centered on the Milky Way and M 31 at 1, 5, 10,
20, 40, and 80% of the peak.
(This figure is available in color in electronic form.) ,
respectively. The contours show the relative
density levels of a combination of two Gaussian distributions with
200 kpc dispersion, centered on the Milky Way and M 31 at 1, 5, 10,
20, 40, and 80% of the peak.
(This figure is available in color in electronic form.) |
![\begin{figure}
{\includegraphics[width=12cm,clip]{ms2407f12.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg191.gif) |
Figure 12:
Properties of the CHVCs entering the simulations described in
Sect. 4. Plotted as a function of H I mass, the images
show the FWHM of the H I distribution, the central H I volume density,
the velocity dispersion of the gas, and the peak column
density. Details of the relation between the H I masses and cloud
properties depend on the dark-matter fraction via the power-law slope
of the H I mass distribution of the CHVC population being modeled: the
dashed lines in the images correspond to a slope
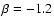 ;
the
solid lines, to a slope of -1.6; and the dotted lines, to a slope
of -2.0. ;
the
solid lines, to a slope of -1.6; and the dotted lines, to a slope
of -2.0. |
3.1 Distribution of CHVCs on the sky
Figure 5 shows the all-sky distribution of the
cataloged CHVCs superimposed on the integrated H I emission observed in
the range -450 <
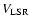 < +400 km s-1, but with
< +400 km s-1, but with
 >70 km s-1. The LDS
catalog and data are used in the north and the HIPASS catalog and data
in the south, with a solid line marking the demarcation at
>70 km s-1. The LDS
catalog and data are used in the north and the HIPASS catalog and data
in the south, with a solid line marking the demarcation at
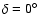 separating the LDS from the HIPASS material. Red
symbols indicate positive LSR velocities and black symbols negative
velocities
separating the LDS from the HIPASS material. Red
symbols indicate positive LSR velocities and black symbols negative
velocities![[*]](/icons/foot_motif.gif) The much higher object density observed in the
southern hemisphere is quite striking, as is the absence of diffuse
emission in the HIPASS MINMED5 data. We comment further below on
the extent to which the CHVC density is a consequence of the differing
observational parameters, especially that of sensitivity.
The much higher object density observed in the
southern hemisphere is quite striking, as is the absence of diffuse
emission in the HIPASS MINMED5 data. We comment further below on
the extent to which the CHVC density is a consequence of the differing
observational parameters, especially that of sensitivity.
To get a better impression of the CHVC clustering and distribution on
the sky, an average density field is constructed; this smoothed field
is more appropriate for comparison with simulated fields, which, as
indicated below, are similarly smoothed. A field of delta functions at
the CHVC locations was convolved with a Gaussian with a dispersion
of 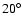 .
The total flux of each delta function is set to unity
for the LDS sources and to the value of the likelihood that such a
particular CHVC would be observed in an LDS-like survey for the HIPASS
sources. Changes in the likelihood relation do not change the overall
picture of the CHVC concentrations; only the contrasts of the
overdensity regions with respect to the average changes.
.
The total flux of each delta function is set to unity
for the LDS sources and to the value of the likelihood that such a
particular CHVC would be observed in an LDS-like survey for the HIPASS
sources. Changes in the likelihood relation do not change the overall
picture of the CHVC concentrations; only the contrasts of the
overdensity regions with respect to the average changes.
Figure 5 shows that the projected density of CHVCs
displays a number of local enhancements. The three most prominent of
these occur in the southern hemisphere, and were previously noted by
Putman et al. (2002) as Groups 1 through 3. Group 1 is
concentrated at the south Galactic pole and extends from about
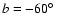 to
to 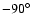 .
It is remarkable for possessing a local
velocity dispersion in excess of 150 km s-1, about twice that seen in any
other part of the sky. This region is bisected by a portion of the
Magellanic Stream and is also spatially coextensive with the nearest
members of the Sculptor group of galaxies (with
.
It is remarkable for possessing a local
velocity dispersion in excess of 150 km s-1, about twice that seen in any
other part of the sky. This region is bisected by a portion of the
Magellanic Stream and is also spatially coextensive with the nearest
members of the Sculptor group of galaxies (with 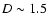 Mpc).
Group 2 is located near
Mpc).
Group 2 is located near
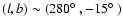 ,
with an
extent of about
,
with an
extent of about
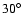 .
This concentration is approximately in the
direction of the leading arm of the Magellanic Clouds but is also near
the Local Group anti-barycenter direction, where the Blitz
et al. (1999) model predicts an enhancement of high-velocity
clouds. Group 3 is centered near
.
This concentration is approximately in the
direction of the leading arm of the Magellanic Clouds but is also near
the Local Group anti-barycenter direction, where the Blitz
et al. (1999) model predicts an enhancement of high-velocity
clouds. Group 3 is centered near
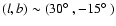 ,
a
region that Wakker & van Woerden (1991) have identified with
the GCN (Galactic Center Negative velocity) population. The most
diffuse concentration, which we label Group 4, is in the northern sky
near
,
a
region that Wakker & van Woerden (1991) have identified with
the GCN (Galactic Center Negative velocity) population. The most
diffuse concentration, which we label Group 4, is in the northern sky
near
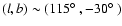 ,
approximately coinciding with
the Local Group barycenter. The Blitz et al. (1999) model
also predicts an enhancement of high-velocity clouds here, albeit a
stronger one than observed. Likewise the mini-halo simulations of
Klypin et al. (1999), Moore et al. (1999,
2001), and Putman & Moore (2002) predict a
strongly enhanced density of low mass objects around the major galaxies
of the Local Group, in particular toward M 31, which lies close to the
barycenter direction. We comment further on the expected strength of
such an enhancement in the observed distribution below.
,
approximately coinciding with
the Local Group barycenter. The Blitz et al. (1999) model
also predicts an enhancement of high-velocity clouds here, albeit a
stronger one than observed. Likewise the mini-halo simulations of
Klypin et al. (1999), Moore et al. (1999,
2001), and Putman & Moore (2002) predict a
strongly enhanced density of low mass objects around the major galaxies
of the Local Group, in particular toward M 31, which lies close to the
barycenter direction. We comment further on the expected strength of
such an enhancement in the observed distribution below.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2407f13.eps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg201.gif) |
Figure 13:
Distances out to which simulated CHVCs would be detected in
the HIPASS survey. The relation between the H I masses and maximum
observable distance depends on the dark-matter fraction via the slope
of the H I mass distribution of the CHVC population. The three curves
refer to clouds with a mass-distribution slope of
-2.0, -1.6, and
-1.2, as dotted, solid, and dashed lines, respectively. The
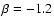 clouds are so diffuse that they fall below the HIPASS
detection threshold for log(
clouds are so diffuse that they fall below the HIPASS
detection threshold for log(
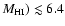 .
The horizontal
lines bracket distances to individual Sculptor Group galaxies. .
The horizontal
lines bracket distances to individual Sculptor Group galaxies. |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2407f14.eps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg202.gif) |
Figure 14:
Distances up to which simulated CHVCs of the indicated total
H I masses would be destroyed by ram-pressure stripping in the
Galactic halo. As an illustration, the limiting distance is calculated
assuming a relative velocity of
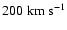 .
The relation
between the H I masses and the stripping distance depends on their
dark-matter content via the slope of the H I mass distribution of the
CHVC population. The dotted curve corresponds to
a slope of .
The relation
between the H I masses and the stripping distance depends on their
dark-matter content via the slope of the H I mass distribution of the
CHVC population. The dotted curve corresponds to
a slope of
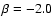 ,
the solid curve to ,
the solid curve to
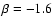 ,
and the
dashed one to a slope
of -1.2. ,
and the
dashed one to a slope
of -1.2. |
3.2 Distribution of CHVCs in velocity
The kinematic properties of the CHVC population provide an important
constraint that must be reproduced by a successful model of the
phenomenon. The kinematic distribution is plotted against Galactic
longitude and latitude, for the Local, Galactic, and Local Group
kinematic reference frames in Figs. 6 and 7,
respectively. The CHVCs are confined within a kinematic envelope
narrower in extent than the
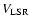 spectral coverage of the surveys; we
stressed above in Sect. 2.2.3 that this confinement is not a
selection effect; it is one of the global kinematic properties of the
ensemble which must be accounted for.
spectral coverage of the surveys; we
stressed above in Sect. 2.2.3 that this confinement is not a
selection effect; it is one of the global kinematic properties of the
ensemble which must be accounted for.
Table 2 shows that the ensemble of clouds has a lower
velocity dispersion in both the GSR and LGSR systems, compared to that
measured in the LSR frame, suggesting that either the Galaxy or the Local
Group might be the natural reference system of the CHVCs. By measuring
the dispersion in the LSR frame, one introduces the solar motion around
the Galactic center into the velocities, which results in a higher
dispersion.
The CHVC groups noted in the previous subsection can also be identified
in the (l,V) and (b,V) distributions. Group 1 is best seen in
Fig. 7 where it gives rise to the very broad velocity
extent in both the GSR and LGSR frames for
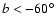 .
Group 2, on
the other hand, is best seen in Fig. 6, centered near
.
Group 2, on
the other hand, is best seen in Fig. 6, centered near
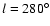 .
This group has a positive mean velocity in the GSR
frame. Only by going to the LGSR frame does the mean group velocity
approach zero. Group 3 is evident in both Figs. 6
and 7. This concentration is seen near
.
This group has a positive mean velocity in the GSR
frame. Only by going to the LGSR frame does the mean group velocity
approach zero. Group 3 is evident in both Figs. 6
and 7. This concentration is seen near
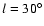 and has a remarkably high negative velocity of about
-200 km s-1 in both the GSR and LGSR frames. Group 4 can also be
distinguished near
and has a remarkably high negative velocity of about
-200 km s-1 in both the GSR and LGSR frames. Group 4 can also be
distinguished near
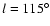 in Fig. 6. This group
also retains a large negative velocity in both the GSR and LGSR frames.
in Fig. 6. This group
also retains a large negative velocity in both the GSR and LGSR frames.
![\begin{figure}
\includegraphics[width=12cm,clip]{ms2407f15.ps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg208.gif) |
Figure 15:
Tidal force for different potentials as a function of
Galactocentric distance. The dashed line corresponds to a point source
with the mass of the Milky Way, the dotted line corresponds to a
potential consistent with a rotation curve flat at the level
of
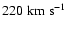 ,
while the solid line corresponds to the
isochrone potential which is used in the simulations to describe the
Milky Way. The dashed horizontal lines correspond to the indicated H I
mass slopes for a cloud mass of ,
while the solid line corresponds to the
isochrone potential which is used in the simulations to describe the
Milky Way. The dashed horizontal lines correspond to the indicated H I
mass slopes for a cloud mass of
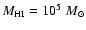 .
Only
for this low cloud mass and the low dark-matter fraction implied by .
Only
for this low cloud mass and the low dark-matter fraction implied by
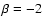 are clouds unstable to tidal disruption.
are clouds unstable to tidal disruption. |
![\begin{figure}
\par {\includegraphics[width=15.1cm,clip]{ms2407f16.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg210.gif) |
Figure 16:
Demonstration of the effects of shot-noise on fit quality,
showing the best- and worst-fitting instances from a sequence of 35 simulations with one of the lowest average 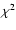 values. The
parameter values are
values. The
parameter values are
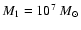 , ,
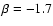 ,
and ,
and
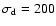 kpc, corresponding to model #9 from
Table 4. The best-fitting instance is plotted on the
right and the worst-fitting on the left. Black lines and symbols are
used for the simulations and red for the observations. Values of kpc, corresponding to model #9 from
Table 4. The best-fitting instance is plotted on the
right and the worst-fitting on the left. Black lines and symbols are
used for the simulations and red for the observations. Values of 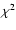 from top to bottom for the best-fitting case are 1.5, 2.2, 3.2, 0.19, and
0.21, respectively; while for the worst-fitting case these are 3.5, 3.3,
5.5, 0.29, and 0.36.
(This figure is available in color in electronic form.) from top to bottom for the best-fitting case are 1.5, 2.2, 3.2, 0.19, and
0.21, respectively; while for the worst-fitting case these are 3.5, 3.3,
5.5, 0.29, and 0.36.
(This figure is available in color in electronic form.) |
Table 2 gives the all-sky statistical parameters of
the CHVC ensemble, calculated by weighting the HIPASS objects with
the likelihood that they would be observed in an LDS-like survey. The
variation of these parameters with the (flux-dependent) relative
weighting of the HIPASS sub-sample is explored by considering both 25%
higher and lower relative sensitivity. Although the dispersion is not
affected strongly by the weighting given to the HIPASS sub-sample, the
mean velocity becomes increasingly negative as the fainter HIPASS
sub-sample receives a higher relative weight.
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f17.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg213.gif) |
Figure 17:
Overview of the spatial and kinematic properties of one of the
best fitting Local Group models from the simulations of
Sect. 4. The simulation, model #9 in
Table 4, has the following parameters:
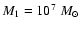 , ,
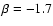 ,
and ,
and
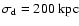 .
The quality
of the fit to the various observables is given by .
The quality
of the fit to the various observables is given by
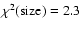 , ,
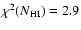 , ,
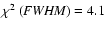 , ,
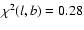 , ,
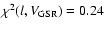 ,
and ,
and
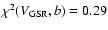 .
The panels provide the same information as
the panels in Fig. 9 for the observed data. The
simulation was sampled with the observational parameters of the LDS and
HIPASS surveys, depending on the declination of the test cloud, as
discussed in the text. The thick-line histograms indicate the LDS
(northern hemisphere) contributions to the total
detections. .
The panels provide the same information as
the panels in Fig. 9 for the observed data. The
simulation was sampled with the observational parameters of the LDS and
HIPASS surveys, depending on the declination of the test cloud, as
discussed in the text. The thick-line histograms indicate the LDS
(northern hemisphere) contributions to the total
detections. |
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f18.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg216.gif) |
Figure 18:
Overview of the spatial and kinematic properties of one of the
best fitting Local Group models from the simulations of
Sect. 4. The simulation, model #3 in
Table 4, has the following parameters:
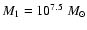 , ,
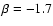 ,
and ,
and
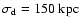 .
The quality of the fit is characterized by .
The quality of the fit is characterized by
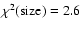 , ,
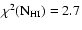 , ,
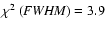 , ,
 , ,
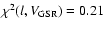 ,
and ,
and
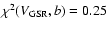 .
The panels provide the same information as the panels
in Fig. 9 for the observed data. The thick-line
histograms indicate the LDS (northern hemisphere) contributions to the
total detections. .
The panels provide the same information as the panels
in Fig. 9 for the observed data. The thick-line
histograms indicate the LDS (northern hemisphere) contributions to the
total detections. |
CHVCs near the galactic equator display the horizontal component of their
space motion. Figure 7 shows that the radial motions
at low |b| are at least as large as those at high latitudes, and
furthermore that the CHVC distribution does not avoid the Galactic
equator, and that substantial positive-velocity amplitudes, as well as
negative-velocity ones, are observed. Large horizontal motions as well
as high positive velocities are difficult to account for in terms of a
galactic fountain model (e.g. Shapiro & Field 1976; Bregman
1980). Similarly, CHVCs located near the galactic poles offer
unambiguous information on the vertical, z, component of their space
motion. The vertical motions are substantial, with positive velocities
approximately equal in number and amplitude to negative velocities; the
vertical motions are of approximately the same amplitude as the
horizontal ones. This situation also is incompatible with
the precepts of the fountain model, which predicts negative Vz velocities
for material returning in a fountain flow. Furthermore, the values of
Vz are predicted to not exceed the velocity of free fall, of some 200 km s-1. In fact,
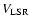 amplitudes substantially larger than the
free-fall value are observed.
amplitudes substantially larger than the
free-fall value are observed.
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f19.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg217.gif) |
Figure 19:
Overview of the spatial and kinematic properties of one of the
best fitting Local Group models before including the effects of
foreground obscuration and SGP exclusion. The simulation, model #9
in Table 4, is shown in Fig. 17 after
applying these effects. The panels provide the same information as the
panels in Fig. 9 for the observed
data. |
Several aspects of the spatial and kinematic topology of the class are
difficult to account for if the CHVCs are viewed as a Milky Way
population, in particular if they are viewed as consequences of a
galactic fountain; these same aspects would seem to discourage a
revival of several of the mechanisms suggested earlier for a Milky Way
population of high-velocity clouds (reviewed, for example, by Oort
1966), including ejection from the Galactic nucleus,
association with a Galactic spiral arm at high latitude, and ejection
following a nearby supernova explosion. We note that the spatial
deployment plotted Fig. 5 shows no preference for the
Galactic equator, nor for the longitudes of the inner Galaxy expected
to harbor most of the disruptive energetic events. CHVCs do not
contaminate the H I terminal-velocity locus in ways which would be
expected if they pervaded the Galactic disk; this observation
constrains the clouds either to be an uncommon component of the Milky
Way disk, confined to the immediate vicinity of the Sun, or else to be
typically at large distances beyond the Milky Way disk. We note also
that the lines of sight in the directions of each of the low |b|CHVCs traverse some tens of kpc of the disk before exiting the Milky
Way: unless one is prepared to accept these CHVCs as boring through the
conventional disk at hypersonic speeds (for which there is no
evidence), and atypical in view of the cleanliness of the
terminal-velocity locus, then their distance is constrained to be
large. We note further that some of the CHVC objects are moving with
velocities in excess of a plausible value of the Milky Way escape
velocity (cf. Oort 1926).
![\begin{figure}
\par {\includegraphics[width=15cm,clip]{ms2407f20.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg218.gif) |
Figure 20:
Three-dimensional distribution of synthetic clouds in the
model #9 simulation of a CHVC population in the Local Group. The
Galaxy and M 31 are indicated with the large black dots, with the Galaxy
at
(x,y,z)=(0,0,0). The axes are labeled in units of Mpc. The smaller
circles indicate all of the objects in the model, whose parameters are
given in Table 4. Not all of the clouds survive the
simulated environment, and not all of those that do survive would be
detected in the LDS and HIPASS observations. The filled black circles
indicated those input clouds that are destroyed by tidal and
ram-pressure stripping influences of M 31 and the Galaxy. The filled
grey circles indicate clouds that are too faint to be detected by the LDS
or by HIPASS, respectively, depending on their declination as viewed from
the origin. The open red circles are the objects that are obscured by the
foreground Galactic H I . Only the filled red circles would be detected in
the combined LDS and HIPASS CHVC sample.
(This figure is available in color in electronic form.) |
Figure 8 shows the average velocity field and velocity
dispersion field, which is constructed in the same way as the average
density field. A field of delta functions was convolved with a
Gaussian with a dispersion of 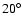 .
The flux of each delta
function was set equal to the measured CHVC velocity and multiplied by
the likelihood that the CHVC would be observed in an LDS-like
survey. The convolved image was then normalized by the density
field. For the velocity dispersion field, a gridded distribution of
squared velocity was similarly generated and the velocity dispersion
was calculated from the square root of the mean squared velocity less
the mean velocity squared,
.
The flux of each delta
function was set equal to the measured CHVC velocity and multiplied by
the likelihood that the CHVC would be observed in an LDS-like
survey. The convolved image was then normalized by the density
field. For the velocity dispersion field, a gridded distribution of
squared velocity was similarly generated and the velocity dispersion
was calculated from the square root of the mean squared velocity less
the mean velocity squared,
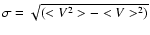 .
The velocity
dispersion field was blanked where the normalized density was below the
mean, since insufficient objects otherwise contribute to the measurement
of local dispersion.
.
The velocity
dispersion field was blanked where the normalized density was below the
mean, since insufficient objects otherwise contribute to the measurement
of local dispersion.
Table 2:
Average velocity and velocity dispersion for the CHVC
ensemble and for the dwarf galaxies in the Local Group, expressed for
three different kinematic reference frames. To correct for the
difference in sensitivity between the LDS and the HIPASS compilations,
the HIPASS CHVCs were weighted by the likelihood that they would be
observed in an LDS-like survey. The three values given for the average
velocity and for the dispersion for the CHVC ensemble for each
reference frame, pertain to an LDS sensitivity 25% lower than the one
shown in Fig. 11 of Paper I, to the same sensitivity, and to a
sensitivity that is 25% higher, respectively. The Local Group data
refer to 27 dwarf galaxies with known radial velocities, from the
tabulation of Mateo (1998).
| |
CHVCs |
CHVCs |
L.G. galaxies |
L.G. galaxies |
| reference frame |
<velocity> |
dispersion |
<velocity> |
dispersion |
| |
(km s-1) |
(km s-1) |
(km s-1) |
(km s-1) |
| |
-33 |
253 |
|
|
| LSR |
-45 |
238 |
-57 |
196 |
| |
-59 |
240 |
|
|
| |
-58 |
128 |
|
|
| GSR |
-63 |
128 |
-22 |
104 |
| |
-69 |
126 |
|
|
| |
-57 |
114 |
|
|
| LGSR |
-60 |
112 |
+4 |
79 |
| |
-65 |
110 |
|
|
Kinematic patterns in the LSR velocity field are dominated by the
contribution of Galactic rotation. After removing the contribution of
Galactic rotation by changing to the GSR reference frame, the following
characteristics of the kinematics of the groups are evident. Relative
minima of
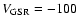 to -175 km s-1 are seen in the directions
of Groups 3 and 4, and a relative maximum of
to -175 km s-1 are seen in the directions
of Groups 3 and 4, and a relative maximum of
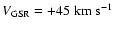 is seen in the vicinity of Group 2. Transforming to
the LGSR frame generally lowers the magnitude of these kinematic
properties (except in the case of Group 3 which becomes more negative
in velocity) although they are all still present. The relative
velocities of Groups 2, 3, and 4 fit into a coherent global pattern
shared by much of the CHVC population, consisting of a strong gradient
in the GSR and LGSR velocity that varies from strongly negative below
the Galactic plane in the first and second quadrants to near zero in
the third and fourth quadrants near the plane.
is seen in the vicinity of Group 2. Transforming to
the LGSR frame generally lowers the magnitude of these kinematic
properties (except in the case of Group 3 which becomes more negative
in velocity) although they are all still present. The relative
velocities of Groups 2, 3, and 4 fit into a coherent global pattern
shared by much of the CHVC population, consisting of a strong gradient
in the GSR and LGSR velocity that varies from strongly negative below
the Galactic plane in the first and second quadrants to near zero in
the third and fourth quadrants near the plane.
The distribution of velocity dispersion is not as strongly effected by
the choice of reference frame since it is a locally defined quantity.
The exception to this rule is near
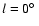 ,
where there are large
gradients in the velocity field, leading to larger apparent dispersions
when sampled with our smoothing kernel. Group 1 is remarkable for its
extremely high velocity dispersion, exceeding that of Groups 2-4 by a
factor of two or more. It is plausible that the Group 1
concentration represents a somewhat different phenomenon than the
remainder of the CHVC sample, as we discuss further below.
,
where there are large
gradients in the velocity field, leading to larger apparent dispersions
when sampled with our smoothing kernel. Group 1 is remarkable for its
extremely high velocity dispersion, exceeding that of Groups 2-4 by a
factor of two or more. It is plausible that the Group 1
concentration represents a somewhat different phenomenon than the
remainder of the CHVC sample, as we discuss further below.
3.3 Summary of the basic observables of the CHVC
ensemble
In the preceding sub-sections we have attempted to correct for the
differing detection levels in the northern and southern hemisphere data
to produce a spatially unbiased estimate of the CHVC distributions in
position and velocity. However, when making comparisons with model
calculations it is possible to explicitly take account of the differing
resolutions and sensitivity of the data in the north and south,
obviating the need to re-weight portions of our sample in advance. The
basic observables from our all-sky sample of CHVCs, without
re-weighting, are shown in Fig. 9 relative to the
GSR frame. The top row of panels represents the density, velocity, and
velocity-dispersion fields, just as in Figs. 5 and 8,
except that the HIPASS sub-sample has not been
re-weighted relative to the LDS. Smoothed versions of the (l,V) and
(V,b) plots shown in Figs. 6 and 7 are
shown in the middle panels of Fig. 9 to facilitate
comparison with the model distributions discussed below. The
distribution of delta functions was convolved with a Gaussian with a
dispersion of 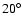 in angle and 20 km s-1 in velocity. Composite
histograms of the peak column density and angular size distributions
for the whole sky are shown in the lower panels of
Fig. 9. Since the LDS and HIPASS survey
resolutions are different (as discussed above in Sect. 2.2.2)
these observables have a different physical implication in the two
hemispheres, but again, these differences can be accounted for
explicitly in the comparison with model distributions.
in angle and 20 km s-1 in velocity. Composite
histograms of the peak column density and angular size distributions
for the whole sky are shown in the lower panels of
Fig. 9. Since the LDS and HIPASS survey
resolutions are different (as discussed above in Sect. 2.2.2)
these observables have a different physical implication in the two
hemispheres, but again, these differences can be accounted for
explicitly in the comparison with model distributions.
![\begin{figure}
{\includegraphics[width=11.5cm,clip]{ms2407f21.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg223.gif) |
Figure 21:
Velocities plotted against galactic longitude for the
ensemble of synthetic clouds corresponding to model #9 of a CHVC
population in the Local Group, whose sky deployment is plotted in
Fig. 17. The red symbols indicate unobscured clouds
which are sufficiently bright to be detected by the Leiden/Dwingeloo or
Parkes surveys, depending on the object declination. Black symbols
refer to simulated clouds which are either too faint to be detected or
obscured. As in the observed velocity, longitude plots of
Fig. 6, the kinematic distributions for the simulated
situation are indicated for three different kinematic reference frames,
namely the LSR (upper), the GSR (middle), and the LGSR (lower
panel).
(This figure is available in color in electronic form.) |
![\begin{figure}
{\includegraphics[width=11.3cm,clip]{ms2407f22.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg224.gif) |
Figure 22:
Velocities plotted against galactic latitude for the ensemble
of synthetic clouds corresponding to model #9 of a CHVC population
in the Local Group. The kinematic distributions are indicated for three
different kinematic reference frames, namely the LSR (upper), the GSR
(middle), and the LGSR (lower panel). As in the simulated (l,V)
distribution of Fig. 21, red symbols indicate
unobscured clouds which are sufficiently bright to be detected by the
Leiden/Dwingeloo or Parkes surveys, depending on the object
declination, while black symbols refer to simulated clouds which are
either too faint to be detected or obscured. The simulated (b,V)
plot may be compared with the observed situation plotted in
Fig. 7.
(This figure is available in color in electronic form.) |


Up: An all-sky study of
Copyright ESO 2002
![\begin{figure}
{\includegraphics[width=12cm,clip]{ms2407f11.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg190.gif)
![\begin{figure}
{\includegraphics[width=12cm,clip]{ms2407f12.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg191.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2407f13.eps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg201.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2407f14.eps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg202.gif)
![\begin{figure}
\includegraphics[width=12cm,clip]{ms2407f15.ps}\end{figure}](/articles/aa/full/2002/35/aa2407/Timg208.gif)
![\begin{figure}
\par {\includegraphics[width=15.1cm,clip]{ms2407f16.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg210.gif)
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f17.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg213.gif)
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f18.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg216.gif)
![\begin{figure}
\par {\includegraphics[width=17cm,clip]{ms2407f19.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg217.gif)
![\begin{figure}
\par {\includegraphics[width=15cm,clip]{ms2407f20.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg218.gif)
![\begin{figure}
{\includegraphics[width=11.5cm,clip]{ms2407f21.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg223.gif)
![\begin{figure}
{\includegraphics[width=11.3cm,clip]{ms2407f22.ps} }
\end{figure}](/articles/aa/full/2002/35/aa2407/Timg224.gif)