

Up: Application of the new
Subsections
Let us now analyze in detail the concepts introduced above.
For the concept of the CEO, consider a rigid celestial sphere, with reference ICRF
Cartesian axes OXYZ with
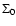 being the intersection of OX with the celestial
sphere, as in Fig. 2. Let P(t) be the instantaneous celestial pole, now called the Celestial
Intermediate Pole (CIP) at time t with Cartesian coordinates
being the intersection of OX with the celestial
sphere, as in Fig. 2. Let P(t) be the instantaneous celestial pole, now called the Celestial
Intermediate Pole (CIP) at time t with Cartesian coordinates
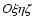 such that
such that
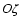 is along OP and
is along OP and 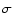 is the point on the equator of P where
is the point on the equator of P where 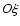 pierces
the sphere. The condition is imposed that for any infinitesimal displacement of P there is
no rotation around
pierces
the sphere. The condition is imposed that for any infinitesimal displacement of P there is
no rotation around 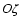 .
Then
.
Then 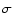 would be the non-rotating origin on the moving
equator of P.
would be the non-rotating origin on the moving
equator of P.
The motion of point P between dates t0 and t is determined by
evaluating the quantity s (t)
![\begin{displaymath}s = [\sigma N] - [\Sigma_{0} N] - ([\sigma _{0} N_{0}] - [\Sigma_{0} N_{0}]) ,
\end{displaymath}](/articles/aa/full/2002/34/aa2452/img38.gif) |
(4) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{FIG2.eps}
\end{figure}](/articles/aa/full/2002/34/aa2452/Timg39.gif) |
Figure 2:
Definition of the CEO on ICRF with motion of the
pole from t0 (P0) to t (P). |
where quantities in brackets are arcs measured on inclined great circles shown
in Fig. 2,
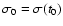 ,
N0 and N are the ascending
nodes of the equators at t0 and t in the equator of the ICRS. Then s
is given by Capitaine et al. (1986, Sect. 5.2):
,
N0 and N are the ascending
nodes of the equators at t0 and t in the equator of the ICRS. Then s
is given by Capitaine et al. (1986, Sect. 5.2):
![\begin{displaymath}s = -\int_{t_0}^t {{X \dot{Y} - Y \dot{X}} \over {1+Z}} {\rm d}t - ([\sigma _{0} N_{0}] -
[\Sigma_{0} N_{0}]) ,
\end{displaymath}](/articles/aa/full/2002/34/aa2452/img41.gif) |
(5) |
where X, Y and Z are the coordinates of the pole and the dots denote their time
derivative. In polar coordinates, if D is the angle
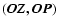 and E is the angle
of the plane
and E is the angle
of the plane 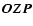 with respect to the principal plane
with respect to the principal plane 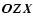 ,
the equation is
,
the equation is
![\begin{displaymath}s = \int_{t_0}^t (\cos D - 1) {\dot E} {\rm d}t -([\sigma_{0} N_0] - [\Sigma_{0} N_0]).
\end{displaymath}](/articles/aa/full/2002/34/aa2452/img45.gif) |
(6) |
The convention may be adopted that 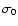 is on the true equator at epoch t0 and
is on the true equator at epoch t0 and
![$[\sigma _{0} N_{0}] = [\Sigma_{0} N_{0}]$](/articles/aa/full/2002/34/aa2452/img47.gif) .
Then
.
Then
![$[\sigma _{0} N_{0}]$](/articles/aa/full/2002/34/aa2452/img48.gif) is the
constant s(t0) in the integral. Then,
is the
constant s(t0) in the integral. Then,
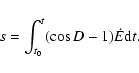 |
(7) |
For the period 1975-2025, the development of s(t) including all terms
exceeding 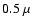 as is, in
as is, in 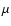 as (Capitaine et al. 2000):
as (Capitaine et al. 2000):
where t is expressed in centuries since J2000.0 (t0=0) and where 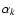 and Ck
are given in Table 1. To extend the development for the periods 1900-1975 and 2025-2100 for
terms exceeding
and Ck
are given in Table 1. To extend the development for the periods 1900-1975 and 2025-2100 for
terms exceeding 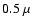 as, add in
as, add in 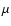 as:
as:
where 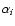 and Di are given in Table 1. In this table and in Eqs. (8) and (9), the notations, referred to the ICRF axes and the corresponding fixed
ecliptic are:
and Di are given in Table 1. In this table and in Eqs. (8) and (9), the notations, referred to the ICRF axes and the corresponding fixed
ecliptic are:
-
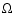 :
mean longitude of the node of the lunar orbit;
:
mean longitude of the node of the lunar orbit;
- L:
mean longitude of the Sun;
- L':
mean longitude of the Moon;
- l:
mean anomaly of the Sun (
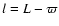 )
where
)
where 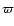 is the mean longitude
of the Sun's perigee;
is the mean longitude
of the Sun's perigee;
- l':
mean anomaly of the Moon (
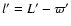 ),
),
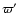 being the mean longitude of the Moon's perigee.
being the mean longitude of the Moon's perigee.
At present, the uncertainty of these expressions is smaller than 1 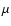 as and is
insensitive to expected modifications of the nutation-precession theory to about this level.
A maximum error of 3
as and is
insensitive to expected modifications of the nutation-precession theory to about this level.
A maximum error of 3 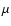 as could be reached in 2100 (Capitaine et al. 2002).
as could be reached in 2100 (Capitaine et al. 2002).
For Earth orientation, the concept of the CEO must be applied to both the celestial
and the terrestrial reference systems. So, a Terrestrial Ephemeris Origin (TEO) was introduced.
The definitions are similar. The formula giving the shift of TEO is
 |
(10) |
where F and g are the polar coordinates of the Earth's pole at time t, and 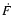 is the time derivative of F. Because of the very small magnitude of the polar displacements,
this is a very small correction (smaller than 0.1 mas next century) that must however
be evaluated from the measurement of the polar motion, when
is the time derivative of F. Because of the very small magnitude of the polar displacements,
this is a very small correction (smaller than 0.1 mas next century) that must however
be evaluated from the measurement of the polar motion, when 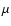 as accuracies are sought.
as accuracies are sought.
In the ICRS system the equivalent of sidereal time is the hour angle
of the celestial ephemeris origin (CEO), and hence is subject only to the
motions of that origin. It is called the Stellar Angle or Earth Rotation Angle.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{FIG3.eps}
\end{figure}](/articles/aa/full/2002/34/aa2452/Timg75.gif) |
Figure 3:
Definition of the stellar angle. |
The Stellar Angle in Fig. 3 is defined by the angle 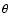 measured along
the equator of the Celestial Intermediate Pole (CIP) between the TEO and the
CEO positively in the retrograde direction. The definition of the CEO
ensures that the derivative
measured along
the equator of the Celestial Intermediate Pole (CIP) between the TEO and the
CEO positively in the retrograde direction. The definition of the CEO
ensures that the derivative
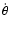 is strictly equal to the instantaneous
angular velocity
is strictly equal to the instantaneous
angular velocity 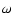 of the Earth around the CIP. Thus,
of the Earth around the CIP. Thus, 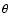 represents
rigorously the sidereal rotation of the Earth around its axis and is such
that UT1 is linearly proportional to the angle. The definition of UT1 by its
relationship with mean sidereal time is proportional to
represents
rigorously the sidereal rotation of the Earth around its axis and is such
that UT1 is linearly proportional to the angle. The definition of UT1 by its
relationship with mean sidereal time is proportional to 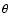 ,
but has additional
terms that take account of precession. Thus, with the CEO the definition of UT1 is such
that the time derivative of UT1 is proportional to
,
but has additional
terms that take account of precession. Thus, with the CEO the definition of UT1 is such
that the time derivative of UT1 is proportional to 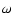 .
.
The numerical relationship between the Stellar Angle and UT1 has
been derived (Capitaine et al. 2000) to be consistent with the conventional
relationship between GMST and UT1. This provides the definition of UT1 for
the ICRF. To an accuracy of 1 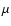 as the relationship is
as the relationship is
where
The coordinate transformation from a unit vector
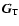 of the ITRS to a unit
vector
of the ITRS to a unit
vector
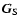 of the GCRS at date t can be given as
of the GCRS at date t can be given as
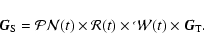 |
(12) |
In this equation, the fundamental components (
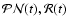 ,
and
,
and
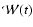 )
are the transformation matrices arising from the motion of the CIP in the ICRF due to
precession-nutation expressions, from the rotation of the Earth around the CIP, and
from polar motion, respectively. They are given in the similar manner to
that given in the IERS Conventions 1996 (McCarthy 1996):
)
are the transformation matrices arising from the motion of the CIP in the ICRF due to
precession-nutation expressions, from the rotation of the Earth around the CIP, and
from polar motion, respectively. They are given in the similar manner to
that given in the IERS Conventions 1996 (McCarthy 1996):
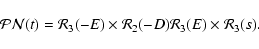 |
(13) |
In these equations, u and v are the coordinates of the CIP in the ITRF, s' is
the shift of TEO defined by Eq. (10), and 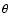 is the Stellar Angle. The quantities
D, E and s are defined in Sect. 7.1. We have used the notation
is the Stellar Angle. The quantities
D, E and s are defined in Sect. 7.1. We have used the notation
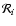 ,
i=1,2,3 for the matrix rotation respectively around the axes x,y,z.
,
i=1,2,3 for the matrix rotation respectively around the axes x,y,z.
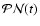 can also be given in an equivalent form directly from the
coordinates X and Y as:
can also be given in an equivalent form directly from the
coordinates X and Y as:
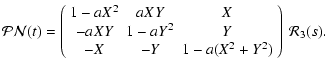 |
|
|
(14) |
with
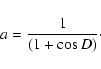 |
(15) |
The latter can also be written with sufficient accuracy as
In addition to the new definitions presented in the previous sections, the IAU has
adopted a new model for precession and nutation based on the work of Mathews et al. (2002).
It is presented in the form of series for nutation in longitude
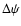 and
obliquity
and
obliquity
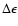 .
There are two versions: the IAU 2000A series provides the
position of the CIP in the GCRF with an accuracy of 0.1 mas (IERS 2002).
A shorter version, accurate to 1 mas, is the IAU 2000B series.
.
There are two versions: the IAU 2000A series provides the
position of the CIP in the GCRF with an accuracy of 0.1 mas (IERS 2002).
A shorter version, accurate to 1 mas, is the IAU 2000B series.
To derive the position (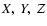 )
of the CIP, the following procedure can be applied
(IERS 2002). One has:
)
of the CIP, the following procedure can be applied
(IERS 2002). One has:
X=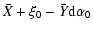 |
Y=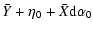 |
(16) |
where
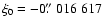 and
and
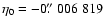 are the celestial pole
offsets at the basic epoch (J2000.0) and d
are the celestial pole
offsets at the basic epoch (J2000.0) and d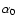 is the right ascension of the mean
equinox, and where:
is the right ascension of the mean
equinox, and where:
In these equations,
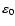 is the obliquity of the ecliptic at J2000. One can compute
is the obliquity of the ecliptic at J2000. One can compute
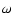 and
and 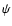 from the precession-nutation series by:
from the precession-nutation series by:
Here,
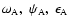 and
and
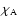 are the precession
quantities of the model given as polynomials of time.
are the precession
quantities of the model given as polynomials of time.


Up: Application of the new
Copyright ESO 2002
![]() ,
N0 and N are the ascending
nodes of the equators at t0 and t in the equator of the ICRS. Then s
is given by Capitaine et al. (1986, Sect. 5.2):
,
N0 and N are the ascending
nodes of the equators at t0 and t in the equator of the ICRS. Then s
is given by Capitaine et al. (1986, Sect. 5.2):
![\begin{displaymath}s = -\int_{t_0}^t {{X \dot{Y} - Y \dot{X}} \over {1+Z}} {\rm d}t - ([\sigma _{0} N_{0}] -
[\Sigma_{0} N_{0}]) ,
\end{displaymath}](/articles/aa/full/2002/34/aa2452/img41.gif)
![\begin{displaymath}s = \int_{t_0}^t (\cos D - 1) {\dot E} {\rm d}t -([\sigma_{0} N_0] - [\Sigma_{0} N_0]).
\end{displaymath}](/articles/aa/full/2002/34/aa2452/img45.gif)
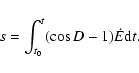
![]() as and is
insensitive to expected modifications of the nutation-precession theory to about this level.
A maximum error of 3
as and is
insensitive to expected modifications of the nutation-precession theory to about this level.
A maximum error of 3 ![]() as could be reached in 2100 (Capitaine et al. 2002).
as could be reached in 2100 (Capitaine et al. 2002).

![]() as the relationship is
as the relationship is
![]() of the ITRS to a unit
vector
of the ITRS to a unit
vector
![]() of the GCRS at date t can be given as
of the GCRS at date t can be given as
![]() can also be given in an equivalent form directly from the
coordinates X and Y as:
can also be given in an equivalent form directly from the
coordinates X and Y as:
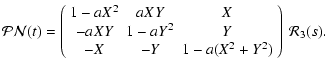
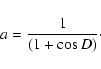
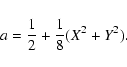
![]() )
of the CIP, the following procedure can be applied
(IERS 2002). One has:
)
of the CIP, the following procedure can be applied
(IERS 2002). One has: