

Up: Application of the new
The coordinates 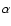 and
and 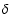 in the intermediate or true system described in the
previous section have the same definition as true coordinates in the equinox-based
system. They are positions with respect to the true, or intermediate, equator and
either the CEO or the equinox, depending upon which system is used. Thus, precession-nutation has
been applied to ICRF positions. This is an extension of the use of the intermediary frame to
astrometry and it is legitimate to call the resulting
in the intermediate or true system described in the
previous section have the same definition as true coordinates in the equinox-based
system. They are positions with respect to the true, or intermediate, equator and
either the CEO or the equinox, depending upon which system is used. Thus, precession-nutation has
been applied to ICRF positions. This is an extension of the use of the intermediary frame to
astrometry and it is legitimate to call the resulting 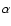 and
and 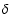 ,
the true geocentric
coordinates and to call the frame, true celestial frame. Their determination from raw observations
corrected for instrumental parameters, stellar aberration, and refraction, and reduced, if
significant, to the geocenter, is analogous to the following procedure, described by Lieske et al.
(1977).
,
the true geocentric
coordinates and to call the frame, true celestial frame. Their determination from raw observations
corrected for instrumental parameters, stellar aberration, and refraction, and reduced, if
significant, to the geocenter, is analogous to the following procedure, described by Lieske et al.
(1977).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{FIG1.eps}
\end{figure}](/articles/aa/full/2002/34/aa2452/Timg24.gif) |
Figure 1:
The precession angles
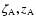 ,
and ,
and
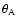 .
The Ox axis points
towards .
The Ox axis points
towards 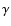 in the old system, towards
in the old system, towards 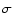 in the new.
in the new. |
For the old system, let us consider a set of three-dimensional reference
Cartesian coordinate axes R0 (0 x y z ) at epoch t0, centered at the center of the
celestial sphere. The X-axis points to the fixed equinox 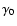 .
The Y-axis is
.
The Y-axis is
 away in an easterly direction along the equator, and the Z-axis points
toward the mean pole P0 (Fig. 1). Let P be the pole of the instantaneous (true
geocentric) reference frame R(t) (O x y z ) at time t and, on its equator, the mean
equinox of date,
away in an easterly direction along the equator, and the Z-axis points
toward the mean pole P0 (Fig. 1). Let P be the pole of the instantaneous (true
geocentric) reference frame R(t) (O x y z ) at time t and, on its equator, the mean
equinox of date, 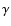 ,
is the origin of right ascensions. The transformation from R0 to
R(t) consists of three rotations.
,
is the origin of right ascensions. The transformation from R0 to
R(t) consists of three rotations.
- 1.
- A rotation of
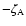 about the Z-axis makes
about the Z-axis makes
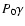 pass through P. This
great circle meets the mean equator of epoch at right angles at point Q and the
mean equator of date at right angles at R. The new x-axis is now in the
direction Q and the y-axis points toward the node S, where the two equators
cross;
pass through P. This
great circle meets the mean equator of epoch at right angles at point Q and the
mean equator of date at right angles at R. The new x-axis is now in the
direction Q and the y-axis points toward the node S, where the two equators
cross;
- 2.
- a rotation of
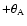 equal to the angular separation of P from P0 about the
new y-axis brings the mean equator of epoch to the mean equator of date. The
new z-axis points to the pole of date P, the y-axis to the node S, and the
x-axis now points towards R in the plane of the equator of date;
equal to the angular separation of P from P0 about the
new y-axis brings the mean equator of epoch to the mean equator of date. The
new z-axis points to the pole of date P, the y-axis to the node S, and the
x-axis now points towards R in the plane of the equator of date;
- 3.
- a rotation of
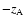 equal to the angle
equal to the angle
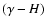 about the new z-axis
brings H to
about the new z-axis
brings H to 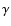 ,
so that the x-axis points toward
,
so that the x-axis points toward 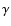 ,
the equinox of date,
and still lies in the plane of the mean equator of date.
,
the equinox of date,
and still lies in the plane of the mean equator of date.
In the new system, the situation is technically similar. Now, in Fig. 1, the geocentric ICRF
axes replace R0, and 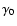 is the origin of right ascensions, while
is the origin of right ascensions, while 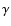 is
replaced by the CEO
is
replaced by the CEO 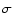 .
Thus, the first two rotations
.
Thus, the first two rotations
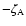 and
and
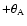 are similar.
Only the third,
are similar.
Only the third,
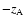 ,
is changed, and is now equal to the angle
,
is changed, and is now equal to the angle
![$[\sigma ,H]$](/articles/aa/full/2002/34/aa2452/img32.gif) .
.
As for 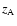 ,
,
![$[\sigma ,H]$](/articles/aa/full/2002/34/aa2452/img32.gif) will be provided by the precession-nutation expressions
(which include the geodesic precession-nutation). Actually, the transformation can be made
in a much simpler manner. Now, continuous VLBI observations systematically provide the
position of P in the ICRF, just as is the case for many years of the polar motion. So,
just as one used to correct for polar motion using the positions of the terrestrial
pole, similarly, one should compute the coordinates in the geocentric ICRF
using the observed position of P (
will be provided by the precession-nutation expressions
(which include the geodesic precession-nutation). Actually, the transformation can be made
in a much simpler manner. Now, continuous VLBI observations systematically provide the
position of P in the ICRF, just as is the case for many years of the polar motion. So,
just as one used to correct for polar motion using the positions of the terrestrial
pole, similarly, one should compute the coordinates in the geocentric ICRF
using the observed position of P (
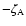 and
and
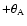 )
and of the CEO (
)
and of the CEO (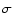 ).
It is necessary that the method and values for the reduction of observations be documented and
referenced.
).
It is necessary that the method and values for the reduction of observations be documented and
referenced.


Up: Application of the new
Copyright ESO 2002
![]() and
and ![]() in the intermediate or true system described in the
previous section have the same definition as true coordinates in the equinox-based
system. They are positions with respect to the true, or intermediate, equator and
either the CEO or the equinox, depending upon which system is used. Thus, precession-nutation has
been applied to ICRF positions. This is an extension of the use of the intermediary frame to
astrometry and it is legitimate to call the resulting
in the intermediate or true system described in the
previous section have the same definition as true coordinates in the equinox-based
system. They are positions with respect to the true, or intermediate, equator and
either the CEO or the equinox, depending upon which system is used. Thus, precession-nutation has
been applied to ICRF positions. This is an extension of the use of the intermediary frame to
astrometry and it is legitimate to call the resulting ![]() and
and ![]() ,
the true geocentric
coordinates and to call the frame, true celestial frame. Their determination from raw observations
corrected for instrumental parameters, stellar aberration, and refraction, and reduced, if
significant, to the geocenter, is analogous to the following procedure, described by Lieske et al.
(1977).
,
the true geocentric
coordinates and to call the frame, true celestial frame. Their determination from raw observations
corrected for instrumental parameters, stellar aberration, and refraction, and reduced, if
significant, to the geocenter, is analogous to the following procedure, described by Lieske et al.
(1977).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{FIG1.eps}
\end{figure}](/articles/aa/full/2002/34/aa2452/Timg24.gif)
![]() ,
,
![]() will be provided by the precession-nutation expressions
(which include the geodesic precession-nutation). Actually, the transformation can be made
in a much simpler manner. Now, continuous VLBI observations systematically provide the
position of P in the ICRF, just as is the case for many years of the polar motion. So,
just as one used to correct for polar motion using the positions of the terrestrial
pole, similarly, one should compute the coordinates in the geocentric ICRF
using the observed position of P (
will be provided by the precession-nutation expressions
(which include the geodesic precession-nutation). Actually, the transformation can be made
in a much simpler manner. Now, continuous VLBI observations systematically provide the
position of P in the ICRF, just as is the case for many years of the polar motion. So,
just as one used to correct for polar motion using the positions of the terrestrial
pole, similarly, one should compute the coordinates in the geocentric ICRF
using the observed position of P (
![]() and
and
![]() )
and of the CEO (
)
and of the CEO (![]() ).
It is necessary that the method and values for the reduction of observations be documented and
referenced.
).
It is necessary that the method and values for the reduction of observations be documented and
referenced.