

Up: Application of the new
The rotation of the Earth is ideally represented in geocentric coordinates
by a transformation matrix 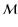 between a terrestrial reference system and the
celestial reference system. In practice, the terrestrial system is the
International Terrestrial Reference System (ITRS) defined by the
International Union for Geodesy and Geophysics (IUGG 1992) and represented physically
by the International Terrestrial Reference Frame (ITRF), which is a
catalogue of positions and velocities of point marks on the Earth. The latest
version is ITRF-2000 (Altamimi et al. 2002). The celestial system is, of
course, the ICRS.
between a terrestrial reference system and the
celestial reference system. In practice, the terrestrial system is the
International Terrestrial Reference System (ITRS) defined by the
International Union for Geodesy and Geophysics (IUGG 1992) and represented physically
by the International Terrestrial Reference Frame (ITRF), which is a
catalogue of positions and velocities of point marks on the Earth. The latest
version is ITRF-2000 (Altamimi et al. 2002). The celestial system is, of
course, the ICRS.
Now, just as was traditionally done, the transformation is made in two
steps. First, the correction for polar motion is described by a matrix 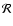 transforming ITRS into an Intermediate Reference System defined by the
Celestial Intermediate Pole (CIP), the corresponding celestial equator, and the
Celestial Ephemeris Origin (CEO). Then, a precession-nutation matrix
transforming ITRS into an Intermediate Reference System defined by the
Celestial Intermediate Pole (CIP), the corresponding celestial equator, and the
Celestial Ephemeris Origin (CEO). Then, a precession-nutation matrix 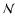 transforms the intermediate system into the ICRS. The difference with the previous
procedure lies only in the definition of the intermediate system. One has, as before:
transforms the intermediate system into the ICRS. The difference with the previous
procedure lies only in the definition of the intermediate system. One has, as before:
The pole is no longer the CEP, but the CIP. The difference is how the
separation is done between polar motion and nutation. The CIP is defined in
such a way that all nutation terms with periods smaller than 2 days are
included in the polar motion. In addition, the subdiurnal tidal polar motion is
taken into account by a model. In practice, the change that will occur on
January 1, 2003, will be transparent to the user: the nutation theory and the
published polar motion will conform to this change. The true equator, which
was defined with respect to the CEP, will now be defined with respect to the
CIP. Actually, the difference is of the order of a few tens of
microarcseconds (Souchay 2000).
The other difference is in the choice of the CEO instead of the mean equinox
on the equator. This choice has at least three advantages:
- 1.
- the difficulties with the equinox, already mentioned in the Introduction,
are removed;
- 2.
- the CEO is defined in such a way that its motion on a fixed celestial
sphere has no component along the equator. This means that the instantaneous movement
of the CEO is always at right-angles to the instantaneous equator
(Guinot 1979); and
- 3.
- the angle
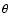 (called Stellar Angle or Earth Rotation Angle) measured on
the equator between the CEO and the longitude origin in the ITRF is such that it yields
UT1 through a strictly linear relationship.
(called Stellar Angle or Earth Rotation Angle) measured on
the equator between the CEO and the longitude origin in the ITRF is such that it yields
UT1 through a strictly linear relationship.
The position of the CEO on the equator is defined by an integral that
involves only the path followed by the precessing-nutating pole since the
reference epoch (Capitaine et al. 1986). This can be computed from the
precession-nutation model and/or observations. Either numerical integration
or an approximate formula given by Capitaine et al. (2000) can be used (see Sect. 7.1).
The CEO motion depends only very slightly upon the pole used as the input
Stellar Angle, or Earth Rotation Angle, is the replacement for Greenwich
Apparent Sidereal Time (GAST). The GAST origin was the equinox, which, in
contrast to the CEO, had components of motion along the equator; these arose
because the equator and ecliptic are moving relative to one another. Consequently, the
relationship between GAST and UT1 included terms due to precession and nutation. The
precession terms appeared in the formula that links Greenwich Mean Sidereal Time (GMST)
and UT1, while the nutation terms appear in the formula GAST= GMST
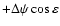 as the equation of the equinoxes. Now, the Stellar Angle does
not depend on precession or nutation (see Sect. 7.3).
as the equation of the equinoxes. Now, the Stellar Angle does
not depend on precession or nutation (see Sect. 7.3).
Remarks:
- 1.
- When introduced by Guinot (1979), the CEO was called a non-rotating origin.
This term is potentially confusing given that the CEO is moving, simply
because the equator, on which it is located, is itself moving. The
"non-rotating'' description refers to the absence of a component of
motion along the equator; the instantaneous motion of the CEO is defined to
be about an axis in the equatorial plane, such that there is no rotation
about the z-axis. Note that this is a kinematical definition. It can be
hard to visualize because there is no geometrical definition and, hence, a diagram
defining where the CEO is at any given time cannot be drawn. The kinematical
definition states how the CEO moves, not where it is. This motion does not depend on
the choice of the system in which the coordinates of the pole of rotation are expressed.
- 2.
- As pointed out by Fukushima (2001), the position of the CEO has a zig-zag
secular motion across the ICRF sky over long periods of time (tens of
thousands of years). However, it is the only choice of origin that gives an
Earth rotation angle formula free from precession-nutation terms; all the
other options listed by Fukushima contain such "crosstalk'' effects to a
greater or lesser degree. The small motion of the CEO is due to the choice of the
constant of integration and the x-axis of the ICRF being near the equinox of J2000.0.
Moreover, the slow secular motion of the CEO has no obvious unfavorable
consequences. Note that the quantity s (formula 8), analogous to the precession in right
ascension, has a secular component mainly due to a t3 term, which
reaches only 40 mas in 2100, and that the CEO is independent of the
celestial reference system adopted.


Up: Application of the new
Copyright ESO 2002
![]() between a terrestrial reference system and the
celestial reference system. In practice, the terrestrial system is the
International Terrestrial Reference System (ITRS) defined by the
International Union for Geodesy and Geophysics (IUGG 1992) and represented physically
by the International Terrestrial Reference Frame (ITRF), which is a
catalogue of positions and velocities of point marks on the Earth. The latest
version is ITRF-2000 (Altamimi et al. 2002). The celestial system is, of
course, the ICRS.
between a terrestrial reference system and the
celestial reference system. In practice, the terrestrial system is the
International Terrestrial Reference System (ITRS) defined by the
International Union for Geodesy and Geophysics (IUGG 1992) and represented physically
by the International Terrestrial Reference Frame (ITRF), which is a
catalogue of positions and velocities of point marks on the Earth. The latest
version is ITRF-2000 (Altamimi et al. 2002). The celestial system is, of
course, the ICRS.
![]() transforming ITRS into an Intermediate Reference System defined by the
Celestial Intermediate Pole (CIP), the corresponding celestial equator, and the
Celestial Ephemeris Origin (CEO). Then, a precession-nutation matrix
transforming ITRS into an Intermediate Reference System defined by the
Celestial Intermediate Pole (CIP), the corresponding celestial equator, and the
Celestial Ephemeris Origin (CEO). Then, a precession-nutation matrix ![]() transforms the intermediate system into the ICRS. The difference with the previous
procedure lies only in the definition of the intermediate system. One has, as before:
transforms the intermediate system into the ICRS. The difference with the previous
procedure lies only in the definition of the intermediate system. One has, as before:
![]() as the equation of the equinoxes. Now, the Stellar Angle does
not depend on precession or nutation (see Sect. 7.3).
as the equation of the equinoxes. Now, the Stellar Angle does
not depend on precession or nutation (see Sect. 7.3).