Two different approaches were used to estimate the CO column density distribution across the cloud. Firstly, we used the traditional way to derive column densities directly from the observed lines by assuming that the excitation temperature for each transition is constant along the line of sight (Sect. 4.1). Secondly, starting from the physical cloud model (see Sect. 2) we used the Monte Carlo radiative transfer program developed by Juvela (1997) to simulate the observed profiles from the cloud. The physical quantities were derived by fitting the calculated spectra to the observed ones (Sect. 4.2). In the following, the two methods and the results are described in detail.
The assumption of a constant excitation temperature
![]() implies that either the
cloud is homogenous (the density and the kinetic temperature are
constant) or that the cloud is isothermal and the transition in
question is thermalised. Even if
this simplistic assumption is
valid, the derivation of the excitation temperatures of the observed isotopic
CO lines involves the following difficulties: 1) The
implies that either the
cloud is homogenous (the density and the kinetic temperature are
constant) or that the cloud is isothermal and the transition in
question is thermalised. Even if
this simplistic assumption is
valid, the derivation of the excitation temperatures of the observed isotopic
CO lines involves the following difficulties: 1) The
![]() CO/C
CO/C
![]() O abundance ratio X has been observed to change from
cloud to cloud, and may also vary from the cloud surface to its
interior parts. This depends on 13C fractionation and selective
photodissociation (see e.g. Bally & Langer 1982; Smith & Adams 1984).
2) The populations of the rotational levels of C
O abundance ratio X has been observed to change from
cloud to cloud, and may also vary from the cloud surface to its
interior parts. This depends on 13C fractionation and selective
photodissociation (see e.g. Bally & Langer 1982; Smith & Adams 1984).
2) The populations of the rotational levels of C
![]() O may deviate from
LTE, i.e. from the situation where a single value of
O may deviate from
LTE, i.e. from the situation where a single value of
![]() describes the relative populations of all J-levels. The populations
are controlled by the collisional excitation and selective
photodissociation mechanisms, which depend on the rotational quantum
number (Warin et al. 1996).
According to Warin et al. (1996) the latter process
causes that low-lying rotational levels are thermalised or
overpopulated and higher levels are subthermally excited. In their
model calculation for a dense dark cloud with a kinetic temperature
of
describes the relative populations of all J-levels. The populations
are controlled by the collisional excitation and selective
photodissociation mechanisms, which depend on the rotational quantum
number (Warin et al. 1996).
According to Warin et al. (1996) the latter process
causes that low-lying rotational levels are thermalised or
overpopulated and higher levels are subthermally excited. In their
model calculation for a dense dark cloud with a kinetic temperature
of
![]() K (see their Figs. 6a-c), the excitation
temperatures of both C
K (see their Figs. 6a-c), the excitation
temperatures of both C
![]() O
O
![]() and
and
![]() CO
CO
![]() lie
close to
lie
close to
![]() ,
whereas
,
whereas
![]()
![]() and all higher
transitions of C
and all higher
transitions of C
![]() O settle between 6 and 7 K.
O settle between 6 and 7 K.
In the derivation of the C18O column densities we have made the following assumptions:
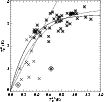 |
Figure 2:
|
![\begin{figure}
\includegraphics[width=11.5cm,clip]{MS2297f3.eps}\end{figure}](/articles/aa/full/2002/31/aa2297/Timg94.gif) |
Figure 3:
C
|
The assumptions 1 and 2
lead to the following
formula for the radiation temperatures at a certain velocity:
![\begin{displaymath}T_\infty \equiv \frac{h\nu}{k} ~ \left[ f_\nu(T_{\rm ex}) - f_\nu(T_{\rm bg}) \right] \; ,
\end{displaymath}](/articles/aa/full/2002/31/aa2297/img97.gif) |
(4) |
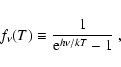 |
(5) |
Using the derived value for
![]()
![]() ,
the excitation
temperature
,
the excitation
temperature
![]()
![]() can be solved from the following
equation for the observed C
can be solved from the following
equation for the observed C
![]() O
O
![]() /
/
![]() integrated intensity ratio:
integrated intensity ratio:
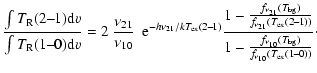 |
(6) |
![\begin{figure}
\par\makebox[\hsize]{\textbf{a)}}\\
\epsfig{file=MS2297f4a.eps, ...
...x[\hsize]{\textbf{b)}}\\
\epsfig{file=MS2297f4b.eps, width=\hsize}
\end{figure}](/articles/aa/full/2002/31/aa2297/Timg105.gif) |
Figure 4:
a) C
|
We have plotted the radial distribution
of the C
![]() O column density
in Fig. 4a. Also shown in this figure is the BES
column density profile
deduced from extinction measurements
(see Sect. 2 and Alves et al. 2001).
After convolving the BES column densities with a 2-dimensional
50
O column density
in Fig. 4a. Also shown in this figure is the BES
column density profile
deduced from extinction measurements
(see Sect. 2 and Alves et al. 2001).
After convolving the BES column densities with a 2-dimensional
50
![]() (full width at half maximum) Gauss function, we can exclude a constant CO
abundance in the gas phase. The difference between the measured and
the smoothed profile
strongly suggests CO depletion in the inner part of B68.
(full width at half maximum) Gauss function, we can exclude a constant CO
abundance in the gas phase. The difference between the measured and
the smoothed profile
strongly suggests CO depletion in the inner part of B68.
To quantify the observed depletion, we assume a depletion law of the
form
Starting from the BES density profile,
we first calculated a depleted column density
distribution for various values of Z, then smoothed the results
to our 50
![]() resolution. Finally, we used the
resolution. Finally, we used the
![]() -method
to scale the theoretical depleted profile to the measured profile,
which corresponds to determining
-method
to scale the theoretical depleted profile to the measured profile,
which corresponds to determining
![]() .
Figure 4b shows the profile with the lowest
.
Figure 4b shows the profile with the lowest
![]() ,
which has Z=180 and
,
which has Z=180 and
![]() .
This profile reproduces the observed profile from
.
This profile reproduces the observed profile from
![]() to
to
![]() almost perfectly.
For small values of Z the fits quickly become worse, with
almost perfectly.
For small values of Z the fits quickly become worse, with
![]() increasing by 15% for Z=50 and by 100% for Z=20.
Larger values of Z cannot be excluded from the
depletion analysis alone, because
increasing by 15% for Z=50 and by 100% for Z=20.
Larger values of Z cannot be excluded from the
depletion analysis alone, because
![]() increases by only a few
percent for
increases by only a few
percent for
![]() .
This is so because for very large Z the scaling (which determines
the gas+dust abundance) can compensate any futher increase in Z.
Only by requiring that
.
This is so because for very large Z the scaling (which determines
the gas+dust abundance) can compensate any futher increase in Z.
Only by requiring that
![]() does not
rise into physically unrealistic regimes we can give an upper limit
for Z, which will be discussed in Sect. 6.
does not
rise into physically unrealistic regimes we can give an upper limit
for Z, which will be discussed in Sect. 6.
We constructed a series of isothermal model clouds with kinetic
temperatures
between 6 and 16 K and distances between 40 and 300 pc,
all with a BES-like
density distribution (
![]() and
and
![]() ).
The radiative transfer problem was
solved with Monte Carlo methods (Juvela 1997).
The radiation
field was simulated with a large number of model photons resulting from
background radiation and emission from within the cloud, where
a microturbulent velocity field was assumed.
The simulations were
used to determine the radiation field in each of the 40 spherical shells into
which the model was divided and to derive new estimates for the level
populations of the molecules. The whole procedure was iterated until the
relative change in the level populations were
).
The radiative transfer problem was
solved with Monte Carlo methods (Juvela 1997).
The radiation
field was simulated with a large number of model photons resulting from
background radiation and emission from within the cloud, where
a microturbulent velocity field was assumed.
The simulations were
used to determine the radiation field in each of the 40 spherical shells into
which the model was divided and to derive new estimates for the level
populations of the molecules. The whole procedure was iterated until the
relative change in the level populations were ![]() 10-4 between
successive iterations.
10-4 between
successive iterations.
The observed C
![]() O spectra were averaged over rings at intervals of
20
O spectra were averaged over rings at intervals of
20
![]() at distances 0
at distances 0
![]() to 100
to 100
![]() from the
selected centre position
RA 17
from the
selected centre position
RA 17
![]() 19
19
![]() 37.
37.![]() 1,
Dec -23
1,
Dec -23
![]() 46
46
![]() 59
59
![]() (1950.0).
The effective
resolution of the averaged C
(1950.0).
The effective
resolution of the averaged C
![]() O
O
![]() and
and
![]() spectra are
60
spectra are
60
![]() and 30
and 30
![]() respectively. Corresponding spectra were
calculated from the models and
averaged with a Gaussian beam to the resolution of the observations. The
correspondence between the observed spectra and the model was measured with a
respectively. Corresponding spectra were
calculated from the models and
averaged with a Gaussian beam to the resolution of the observations. The
correspondence between the observed spectra and the model was measured with a
![]() value summed channel by channel over all spectra. Averaged spectra at
different distances from the centre position were all given equal weight in
the fit.
value summed channel by channel over all spectra. Averaged spectra at
different distances from the centre position were all given equal weight in
the fit.
For each pair of T and D,
two parameters were optimised: the fractional C
![]() O
abundance
O
abundance
![]() and the turbulent line
width. The best fit was obtained for
and the turbulent line
width. The best fit was obtained for
![]() K and
D=80 pc with
K and
D=80 pc with
![]() .
However, this solution still produces
far too little intensity at large offsets, the observed intensity at 100
.
However, this solution still produces
far too little intensity at large offsets, the observed intensity at 100
![]() being more than twice the model prediction.
being more than twice the model prediction.
We further studied a series of models assuming a
non-constant C
![]() O fractional abundance,
O fractional abundance,
![]() ,
in order to account for CO depletion in the cloud centre.
The density dependency was assumed to be
,
in order to account for CO depletion in the cloud centre.
The density dependency was assumed to be
![]() ) ,
as suggested
in the homogenuous model analysis
(Sect. 4.1.3).
For the depletion parameter Z we tried a large range of values
between 4 and 104.
) ,
as suggested
in the homogenuous model analysis
(Sect. 4.1.3).
For the depletion parameter Z we tried a large range of values
between 4 and 104.
As in Sect. 4.1.3, we find Z not to be well
constrained, lying somewhere between 20 and 300. In contrast to our
earlier analysis, we now do find an upper limit for Z, just as we
can give a lower limit. The reason for this is that in the homogenuous
approach, high densities n, which go along with a high Z, do not
influence the excitation conditions (
![]() being determined earlier),
while now the total density n and not only
being determined earlier),
while now the total density n and not only
![]() is taken into
account.
is taken into
account.
For both Z=50 and Z=200, the best fitting values for the distance and the
temperature are 70 pc and 7 K respectively.
Some other specific combinations of Z, D and T within the ranges
Z=20-200,
D=70-120 pc and
T=6-8 K result in almost equally good fits.
The Monte Carlo simulations do not favour a
particular model, as the
![]() values are not significantly
different. They do, however, favour the models including depletion as
compared to the Z=0 ones. For Z in the given range
the
values are not significantly
different. They do, however, favour the models including depletion as
compared to the Z=0 ones. For Z in the given range
the
![]() values are
a factor of 1.6 lower than in the no-depletion models, and the spectra
are well fitted from the centre out to the edge of the cloud.
Figure 5 shows the correspondence between the model and the
observed spectra.
values are
a factor of 1.6 lower than in the no-depletion models, and the spectra
are well fitted from the centre out to the edge of the cloud.
Figure 5 shows the correspondence between the model and the
observed spectra.
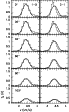 |
Figure 5:
Comparison of observed and modelled spectra.
The observed spectra (histograms) are averages over rings at distances
between 0
|
Copyright ESO 2002