Throughout this paper, we make extensive use of the dust column density profile measured by Alves et al. (2001) and in parts also take up their proposal of B68 being a Bonnor-Ebert sphere (BES). In order to make transparent which assumptions are involved in deriving various quantities, we summarise in this section the concept of Bonnor-Ebert spheres and discuss its applicability to B68.
Assuming an isothermal, spherically symmetric distribution of gas in
hydrostatic
equilibrium, a cloud's density profile is governed by
Eqs. (374) and (375) of
Chandrasekhar (1939, p.156).
As Bonnor (1956) and Ebert (1955) pointed out, these equations
have a family of solutions characterised by the nondimensional radial
parameter
![]() ,
if the sphere is bound by a fixed external pressure
,
if the sphere is bound by a fixed external pressure
![]() .
They also discovered that such a gaseous configuration is
unstable to gravitational collapse if
.
They also discovered that such a gaseous configuration is
unstable to gravitational collapse if
![]() .
With R being the radius where the pressure P(r) has dropped
to
.
With R being the radius where the pressure P(r) has dropped
to
![]() ,
the physical parameters are determined by the scaling relation
,
the physical parameters are determined by the scaling relation
![]() ,
where
,
where
![]() is the central density, a the isothermal sound speed and G
the gravitational constant.
is the central density, a the isothermal sound speed and G
the gravitational constant.
In practice, the radius of a cloud cannot be directly observed,
but only its angular diameter
![]() and in certain circumstances its
distance D.
Using the mean molecular weight m and the central number density
and in certain circumstances its
distance D.
Using the mean molecular weight m and the central number density
![]() to write
to write
![]() and
and
![]() ,
where
k is the
Boltzmann constant and
,
where
k is the
Boltzmann constant and
![]() the kinetic temperature, we can express the
relation
between the
physical parameters of a BES as
the kinetic temperature, we can express the
relation
between the
physical parameters of a BES as
Alves et al. (2001) determined the extinction profile of B68 and found it
to have the same shape as the column density profile of a BES with
![]() .
Does this mean that B68 actually is a BES? First of all, one
has to
assume that the shape of the gas column density profile has
been measured,
i.e.
.
Does this mean that B68 actually is a BES? First of all, one
has to
assume that the shape of the gas column density profile has
been measured,
i.e.
![]() .
Except for Sect. 4.1.2,
all results of this paper implicitly fall back on this assumption.
But despite having the column (and hence number) density profile of a
BES, the globule may still not be a BES in the sense that it may not
be isothermal, it may not be in hydrostatic equilibrium and it
may not be in equilibrium altogether.
It is safe to say that B68 cannot be a perfect BES for a number of
reasons: 1) Its shape is not perfectly circulary symmetric. 2) The
molecular line-widths show that a small microturbulent velocity
field is present. 3) The measured
.
Except for Sect. 4.1.2,
all results of this paper implicitly fall back on this assumption.
But despite having the column (and hence number) density profile of a
BES, the globule may still not be a BES in the sense that it may not
be isothermal, it may not be in hydrostatic equilibrium and it
may not be in equilibrium altogether.
It is safe to say that B68 cannot be a perfect BES for a number of
reasons: 1) Its shape is not perfectly circulary symmetric. 2) The
molecular line-widths show that a small microturbulent velocity
field is present. 3) The measured
![]() is larger than the critical
value, i.e. B68 is unstable to gravitational collapse unless some
additional support mechanism, e.g. a magnetic field, plays a role.
Nevertheless, in the framework of inevitable idealisations in
astronomy, the BES model fits B68 certainly to some degree (as the
density profile fits near-perfectly). We will resume the BES model and
discuss the conclusion from applying it to B68 in
Sect. 6.2. Therefore we
calculate the numerical constants involved in the following
paragraphs. Note that up to and including
Sect. 6.1 we refer with
"cloud model'' and "BES profile'' to the fitted
(column) density profile, which is based on the raw observations of
Alves et al. (2001) and does not require the hydrostatic equilibrium
assumption.
is larger than the critical
value, i.e. B68 is unstable to gravitational collapse unless some
additional support mechanism, e.g. a magnetic field, plays a role.
Nevertheless, in the framework of inevitable idealisations in
astronomy, the BES model fits B68 certainly to some degree (as the
density profile fits near-perfectly). We will resume the BES model and
discuss the conclusion from applying it to B68 in
Sect. 6.2. Therefore we
calculate the numerical constants involved in the following
paragraphs. Note that up to and including
Sect. 6.1 we refer with
"cloud model'' and "BES profile'' to the fitted
(column) density profile, which is based on the raw observations of
Alves et al. (2001) and does not require the hydrostatic equilibrium
assumption.
The extinction profile of B68 only deviates noticeably from a BES
profile in the outermost parts
(for
![]() ,
see Fig. 2 of Alves et al. 2001). As the fitting parameters, particularly
,
see Fig. 2 of Alves et al. 2001). As the fitting parameters, particularly
![]() ,
change considerably if one tries to scale the BES profile to also
those data points, we have done a
,
change considerably if one tries to scale the BES profile to also
those data points, we have done a
![]() -fit to the data of
Alves et al. (2001, who kindly provided us with the data), deliberately
ignoring data points at
-fit to the data of
Alves et al. (2001, who kindly provided us with the data), deliberately
ignoring data points at
![]() at this stage. The lowest
at this stage. The lowest
![]() was found for
was found for
![]() ,
which corresponds to a
centre-to-edge density contrast of
17.1.
The scaling parameters for
this particular BES extinction profile are
,
which corresponds to a
centre-to-edge density contrast of
17.1.
The scaling parameters for
this particular BES extinction profile are
![]() and
and
![]() mag (see also Fig. 4a). The actual
peak extinction value is not needed in Eq. (1), but will be used
in Sects. 5 and 6
to derive the H2-to-extinction
ratio in B68.
Varying
mag (see also Fig. 4a). The actual
peak extinction value is not needed in Eq. (1), but will be used
in Sects. 5 and 6
to derive the H2-to-extinction
ratio in B68.
Varying
![]() by one
decimal increases
by one
decimal increases
![]() by 2%, while the scaling parameters
by 2%, while the scaling parameters
![]() and
and
![]() are modified by 0.6% and 0.3%
respectively. The density contrast, being an
increasing function of
are modified by 0.6% and 0.3%
respectively. The density contrast, being an
increasing function of
![]() ,
is the least precise parameter,
changing between 16.5 and 17.7 for the given variation of
,
is the least precise parameter,
changing between 16.5 and 17.7 for the given variation of
![]() .
.
For a BES with
![]() and
and
![]() ,
we have calculated the following values
for the radius R, the central gas particle number
density
,
we have calculated the following values
for the radius R, the central gas particle number
density
![]() ,
the peak column
density
,
the peak column
density
![]() ,
the total mass M and the external pressure
,
the total mass M and the external pressure
![]() :
:
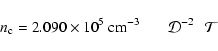
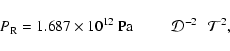
We assume H2 and He are the only species
contributing substantially to mass and pressure, with a fractional
helium abundance of
![]() .
Under this assumption, the mean
molecular weight is m = 2.329
.
Under this assumption, the mean
molecular weight is m = 2.329
![]() (
(
![]() being the atomic
hydrogen mass).
Throughout this paper, we use the commonly used rounded value
m=2.33
being the atomic
hydrogen mass).
Throughout this paper, we use the commonly used rounded value
m=2.33
![]() .
For other values of m, the quantities in
Eq. (2) have to be scaled as
.
For other values of m, the quantities in
Eq. (2) have to be scaled as
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
If two of the three remaining unknown variables (D, T and
![]() )
in Eq. (1) are known, the third one follows from
Eq. (1) and the cloud model is fixed.
This way we first calculated
)
in Eq. (1) are known, the third one follows from
Eq. (1) and the cloud model is fixed.
This way we first calculated
![]() in Eq. (2), then
from the fixed cloud model we determined
in Eq. (2), then
from the fixed cloud model we determined
![]() and M.
If all three variables D, T and
and M.
If all three variables D, T and
![]() can be determined from
observations, Eq. (1) allows a consistency check of the
involved parameters.
In practice, for a small globule like B68
both T and
can be determined from
observations, Eq. (1) allows a consistency check of the
involved parameters.
In practice, for a small globule like B68
both T and
![]() can be
determined to some accuracy e.g. by ammonia observations, while
a distance estimate remains difficult due to the
lack of foreground stars. In fact,
Eq. (1) can be used to determine the
distance under these circumstances.
can be
determined to some accuracy e.g. by ammonia observations, while
a distance estimate remains difficult due to the
lack of foreground stars. In fact,
Eq. (1) can be used to determine the
distance under these circumstances.
Copyright ESO 2002