 |
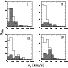
Figure 3:
Distribution of Ts and Ms (hatched)
as a function of
|
 |
Figure 3:
Distribution of Ts and Ms (hatched)
as a function of
|
As far as kinematical properties are concerned, Fig. 2 shows the
distribution of the average extension (
![]() )
for
Ts (solid histogram) and Ms (hatched) in the four subsamples.
Ts appear more compact than Ms in all but the first subsample.
However, according to the KS test, differences in
)
for
Ts (solid histogram) and Ms (hatched) in the four subsamples.
Ts appear more compact than Ms in all but the first subsample.
However, according to the KS test, differences in
![]() between
Ts and Ms are not significant (59%, 56% and 77% c.l. respectively).
This is not unexpected, given our selection criteria,
and actually confirms that we sample Ts and Ms on a common scale.
When
between
Ts and Ms are not significant (59%, 56% and 77% c.l. respectively).
This is not unexpected, given our selection criteria,
and actually confirms that we sample Ts and Ms on a common scale.
When
![]() rather than
rather than
![]() is examined
differences get significant (above 90% c.l.) in subsamples II and III.
While
is examined
differences get significant (above 90% c.l.) in subsamples II and III.
While ![]() 40% of the Ms include a member which is
at a distance larger than 150 h-1 kpc from the center,
this is the case for less than 7% of Ts.
The excess of Ms with members close to the
limiting distance, together with the high fraction of
Ms among rejected non symmetric CGs, possibly indicates that we are
sampling subclumps embedded
in larger structures eventhough the external limit of 200
40% of the Ms include a member which is
at a distance larger than 150 h-1 kpc from the center,
this is the case for less than 7% of Ts.
The excess of Ms with members close to the
limiting distance, together with the high fraction of
Ms among rejected non symmetric CGs, possibly indicates that we are
sampling subclumps embedded
in larger structures eventhough the external limit of 200
![]() kpc
imposed by the algorithm prevents from drawing definite
conclusions concerning any typical dimensions for Ms.
In the cz range between 2500 and 7500 km s-1, including
60% of Ms,
the average dimension of CGs increases with multiplicity following
the relation
kpc
imposed by the algorithm prevents from drawing definite
conclusions concerning any typical dimensions for Ms.
In the cz range between 2500 and 7500 km s-1, including
60% of Ms,
the average dimension of CGs increases with multiplicity following
the relation
![]() .
This relation has been derived
for the median number of galaxies in multiplets which is 4.5.
The velocity dispersion of galaxies in a bound system provides
an estimate of the potential well, although in CGs errors caused by random
orientation of the system along the line of sight might dominate the result.
In any case values obtained on a large sample of CGs are less affected by
this bias, and thus yield more reliable results.
In Fig. 3 the distributions of Ts and Ms relative to the parameter
.
This relation has been derived
for the median number of galaxies in multiplets which is 4.5.
The velocity dispersion of galaxies in a bound system provides
an estimate of the potential well, although in CGs errors caused by random
orientation of the system along the line of sight might dominate the result.
In any case values obtained on a large sample of CGs are less affected by
this bias, and thus yield more reliable results.
In Fig. 3 the distributions of Ts and Ms relative to the parameter
![]() are shown. Distributions are different at
61%, 99.6%, 97% and 98% c.l. respectively.
Comparison of
are shown. Distributions are different at
61%, 99.6%, 97% and 98% c.l. respectively.
Comparison of
![]() yields obviously more significant
differences (98%, 99.99%, 99.9% and 99.8% c.l.).
Considering again CGs within the range 2500-7500 km s-1, we find
yields obviously more significant
differences (98%, 99.99%, 99.9% and 99.8% c.l.).
Considering again CGs within the range 2500-7500 km s-1, we find
![]() to increase with multiplicity as
to increase with multiplicity as
![]() .
.
Next, before estimating the mass associated with CGs,
we check whether and how many CGs in the sample satisfy the
necessary (but not sufficient) criterion
for a galaxy system to be virialized.
In Fig. 4
![]() as a function of
as a function of
![]() for Ts and Ms is plotted.
for Ts and Ms is plotted.
![]() is computed according to prescriptions in
is computed according to prescriptions in
![]() CDM (
CDM (
![]() ,
,
![]() )
cosmologies, requiring a virialized system to
display an overdensity greater than 333 with respect to the mean density
of the universe.
Figure 4 shows that most CGs (95%) in the
sample satisfy the virialization condition and might therefore be
physical bound systems. Had we compared
)
cosmologies, requiring a virialized system to
display an overdensity greater than 333 with respect to the mean density
of the universe.
Figure 4 shows that most CGs (95%) in the
sample satisfy the virialization condition and might therefore be
physical bound systems. Had we compared
![]() with the harmonic radius, the fraction of virialized systems
would be slightly lower (90%).
with the harmonic radius, the fraction of virialized systems
would be slightly lower (90%).
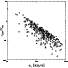 |
Figure 4:
Ratio of average dimension
|
Concerning the real nature of CGs it must also
be stressed that the median velocity
dispersion associated with galaxies in Ts (Table 3) is comparable to the
mean galaxy-galaxy velocity difference associated with field galaxies
(Somerville et al. 1996; Fisher et al. 1994). Accordingly one could speculate that
the Ts sample suffers from serious contamination by pseudo-structures
of unrelated field galaxies (filaments viewed nearly edge on),
in which redshift tracing the Hubble flow is used to compute
a velocity dispersion. If this is the case
the contamination by interlopers is expected to bias the velocity
dispersion of Ts towards the low end.
However the exclusion of suspiciously low-![]() systems
would also cause any genuine bound CG representing a system in its
final state of coalescence to be excluded from the sample.
In our sample the fraction of low
systems
would also cause any genuine bound CG representing a system in its
final state of coalescence to be excluded from the sample.
In our sample the fraction of low
![]() CGs
(i.e.
CGs
(i.e.
![]() km s-1) turns out to be
32% and 16% among Ts and Ms.
The first value is slightly lower than the
40% unbound Triplets claimed by Diaferio (2000).
Figures are roughly
consistent given that Diaferio selects systems with a FoF algorithm,
which, when applied to small systems, tends to return an excess of
elongated structures displaying enhanced contamination by outliers.
Concerning Ms, the bias induced by interlopers might well
push the velocity dispersion higher so that it is not
obvious how to separate structures contaminated by interlopers from
bound structures.
km s-1) turns out to be
32% and 16% among Ts and Ms.
The first value is slightly lower than the
40% unbound Triplets claimed by Diaferio (2000).
Figures are roughly
consistent given that Diaferio selects systems with a FoF algorithm,
which, when applied to small systems, tends to return an excess of
elongated structures displaying enhanced contamination by outliers.
Concerning Ms, the bias induced by interlopers might well
push the velocity dispersion higher so that it is not
obvious how to separate structures contaminated by interlopers from
bound structures.
The substantial difference in the kinematical characteristics
of Ts and Ms
might affect also parameters directly derived from
![]() and
and
![]() such as estimated mass
(
such as estimated mass
(
![]()
![]() )
and dynamical time
(
)
and dynamical time
(
![]() ).
To compute these quantities we use
).
To compute these quantities we use
![]() instead
of the harmonic radius
instead
of the harmonic radius ![]() ,
because
we select groups according to their maximal extension rather than constraining
their maximum galaxy-galaxy separation.
In Figs. 5 and 6 distributions of estimated M/L and
,
because
we select groups according to their maximal extension rather than constraining
their maximum galaxy-galaxy separation.
In Figs. 5 and 6 distributions of estimated M/L and
![]() are shown.
It appears that Ms possibly display higher M/L and shorter
are shown.
It appears that Ms possibly display higher M/L and shorter
![]() than Ts, even though
differences concerning these quantities are only marginally significant.
The use of the harmonic radius (or of the median galaxy-galaxy separation)
to compute these quantities
would confirm the possible difference,
with significance similar to that obtained
with
than Ts, even though
differences concerning these quantities are only marginally significant.
The use of the harmonic radius (or of the median galaxy-galaxy separation)
to compute these quantities
would confirm the possible difference,
with significance similar to that obtained
with
![]() .
The higher mean M/L associated with Ms could indicate either a higher mean
.
The higher mean M/L associated with Ms could indicate either a higher mean
![]() or a higher fraction of mass between
galaxies.
Concerning
or a higher fraction of mass between
galaxies.
Concerning
![]() ,
the longer values associated
with Ts might indicate that these are systems closer to turnaround,
which are therefore less likely to be virialized.
Alternatively the smaller M/L and higher
,
the longer values associated
with Ts might indicate that these are systems closer to turnaround,
which are therefore less likely to be virialized.
Alternatively the smaller M/L and higher
![]() associated with Ts might well be claimed to arise because of
contamination by interlopers, and hence to be non-physical.
associated with Ts might well be claimed to arise because of
contamination by interlopers, and hence to be non-physical.
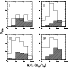 |
Figure 5: M/L distribution of Ts and Ms (hatched). Ms display larger M/L than Ts at 46%, 98%, 87% and 94% c.l. in the four classes. |
 |
Figure 6:
Distribution of Ts and Ms (hatched)
as a function of the dynamical time
|
In summary, the observed kinematical differences between Ts and Ms suggest that globally Ts do not constitute a fair subsample of Ms. Interestingly, differences are not significant between Ts and Ms in sample I, including mainly faint galaxies.
Copyright ESO 2002