

Up: Carbon-rich giants in the function
Subsections
In Paper I was established (Eq. (33)) the relation
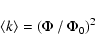 |
(3) |
where 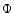 is the true (observed) angular diameter of the star and
is the true (observed) angular diameter of the star and 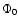 its diameter
would its magnitude be
its diameter
would its magnitude be
![$\left[1.08\right]_{0}=0,$](/articles/aa/full/2002/30/aa2243/img119.gif) other thinks being equal.
other thinks being equal.
The
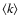 -coefficient is a mean value over the wavelengths used, that is derived directly
from photometry (Knapik et al. 1999, Sect. 2.4). It is thus an angular diameter on a
relative scale as confirmed in Paper I (Sect. 8). It correlates with astrometric data, namely
estimated true parallaxes
-coefficient is a mean value over the wavelengths used, that is derived directly
from photometry (Knapik et al. 1999, Sect. 2.4). It is thus an angular diameter on a
relative scale as confirmed in Paper I (Sect. 8). It correlates with astrometric data, namely
estimated true parallaxes 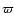 from Knapik et al. (1998; Sect. 4), in the expected
way. The reference angular diameters
from Knapik et al. (1998; Sect. 4), in the expected
way. The reference angular diameters 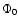 were calibrated as a function of effective
temperatures (Paper I, Sect. 11), viz.
were calibrated as a function of effective
temperatures (Paper I, Sect. 11), viz.
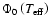 .
The coefficient may
still be written as
.
The coefficient may
still be written as
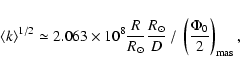 |
(4) |
where R is the photospheric radius of the star. Replacing
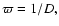 we introduce a new
coefficient
we introduce a new
coefficient
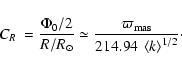 |
(5) |
The latter quantity is a linear and homogeneous function of 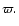 Parallax errors
predominate over photometric errors on
Parallax errors
predominate over photometric errors on
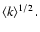 Within a restricted sample,
say in a given photometric group, the distribution of true parallaxes may be assumed Gaussian,
which is also the case of the quantity in Eq. (5). The
Within a restricted sample,
say in a given photometric group, the distribution of true parallaxes may be assumed Gaussian,
which is also the case of the quantity in Eq. (5). The
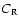 -coefficient can then be
averaged without being affected by the bias described by Smith & Eichhorn (1996).
This is the angular radius (in mas) shown by a star of photometric coefficient
-coefficient can then be
averaged without being affected by the bias described by Smith & Eichhorn (1996).
This is the angular radius (in mas) shown by a star of photometric coefficient
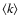 and parallax
and parallax 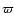 if its magnitude would have been
if its magnitude would have been
![$\left[1.08\right]_{0}=0$](/articles/aa/full/2002/30/aa2243/img127.gif) and its radius have been
and its radius have been
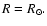 In practice, the third member of Eq. (5) will be used to
evaluate CR, to be averaged for a given group (or class) of stars. The mean values
In practice, the third member of Eq. (5) will be used to
evaluate CR, to be averaged for a given group (or class) of stars. The mean values
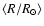 are then evaluated from
are then evaluated from 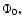 a quantity that correlates
with groups and effective temperatures, and not with
a quantity that correlates
with groups and effective temperatures, and not with
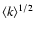 (Paper I).
(Paper I).
Individual estimates of
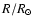 may be derived from individual
may be derived from individual 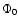 's as quoted
in Paper I or from
's as quoted
in Paper I or from
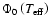 relations, to be replaced in Eq. (5).
They should not be averaged since the corresponding means could be biased.
relations, to be replaced in Eq. (5).
They should not be averaged since the corresponding means could be biased.
The above Eq. (5) can be written as
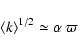 |
(6) |
where
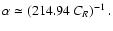 That coefficient is expected to
span a range delineated by those in R and
That coefficient is expected to
span a range delineated by those in R and 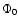 for the considered group. The corresponding
diagram of
for the considered group. The corresponding
diagram of
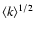 vs.
vs. 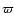 should exhibit a populated interior of an
angle with
vertex at origin. This is the result shown by Knapik et al. (1998) for 34 CV2-stars
(their Fig. 3), whereas the diagram with observed parallaxes
should exhibit a populated interior of an
angle with
vertex at origin. This is the result shown by Knapik et al. (1998) for 34 CV2-stars
(their Fig. 3), whereas the diagram with observed parallaxes
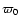 as abscissae did not
have this property. We present here an updated version of the former diagram including 43
CV2-stars and 46 SEDs (Fig.
as abscissae did not
have this property. We present here an updated version of the former diagram including 43
CV2-stars and 46 SEDs (Fig.
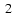 )
that confirms the previous one. The diagrams for
the groups HC0+HC1, HC2 to HC5, CV1, CV3 and CV4 are displayed in Fig.
)
that confirms the previous one. The diagrams for
the groups HC0+HC1, HC2 to HC5, CV1, CV3 and CV4 are displayed in Fig.
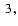 and
CV5 and CV6+CV7 in Fig.
and
CV5 and CV6+CV7 in Fig.
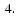 The poorly-documented SCV-group is not shown.
The poorly-documented SCV-group is not shown.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fi2.eps} \end{figure}](/articles/aa/full/2002/30/aa2243/Timg139.gif) |
Figure 2:
The photometric relative angular radii
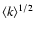 as a function
of true parallaxes
as a function
of true parallaxes 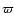 in mas, for the CV2-group.
in mas, for the CV2-group. |
Unfortunately, the number of stars per diagram is rather limited. The group CV2 was studied in
detail. The Gaussian distribution
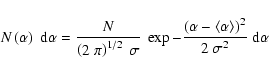 |
(7) |
could be fit around the arithmetic mean
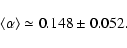 |
(8) |
Despite a large dispersion, a satisfactory solution was found with
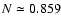 and
and
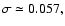 that is
that is
![\begin{displaymath}N\left(\alpha\right)~\rm {d} \alpha \simeq 6.050 \: \exp \left[ -156~\left(\alpha - 0.148
\right)^{2}\right]\;\rm {d}\alpha.
\end{displaymath}](/articles/aa/full/2002/30/aa2243/img168.gif) |
(9) |
Two linear relations shown as full lines in Fig.
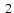 were derived which correspond
roughly to
were derived which correspond
roughly to
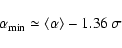 |
(10) |
and
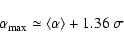 |
(11) |
which results in 83% of data falling inside the materialized sector
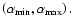 There is no significant departure except
perhaps for
There is no significant departure except
perhaps for
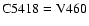 Cyg.
Cyg.
Fits to the other diagrams for HC and CV-groups were also derived, which proved frequently more
difficult to obtain.
The obtained estimates are quoted in Table
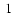 for the sequence of groups in our
classification. They roughly correspond to inferior and superior limits in relative
radii
for the sequence of groups in our
classification. They roughly correspond to inferior and superior limits in relative
radii
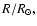 for a given range in
for a given range in 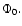 A general increase of both limits is
noticed along the sequence of photometric groups which is moderate till HC3 and then from
CV3 to CV6, where steady extremas at nearly
A general increase of both limits is
noticed along the sequence of photometric groups which is moderate till HC3 and then from
CV3 to CV6, where steady extremas at nearly
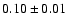 and
and
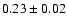 are reached.
Such flattenings at both ends of the sequence will be found again while deriving
luminosities and studying the locus of carbon giants in the HR diagram (Sects. 5 to 7).
are reached.
Such flattenings at both ends of the sequence will be found again while deriving
luminosities and studying the locus of carbon giants in the HR diagram (Sects. 5 to 7).
![\begin{figure}
\par\includegraphics[width=6cm]{f3_1.eps}\includegraphics[width=6...
...aphics[width=6cm]{f3_7.eps}\includegraphics[width=6cm]{f3_8.eps}\par\end{figure}](/articles/aa/full/2002/30/aa2243/Timg180.gif) |
Figure 3:
Same diagram as Fig.
 for the groups HC0+HC1, HC2 to HC5, and CV1,
CV3 and CV4.
for the groups HC0+HC1, HC2 to HC5, and CV1,
CV3 and CV4. |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{f4_1.eps}\includegraphics[width=6cm,clip]{f4_2.eps}
\end{figure}](/articles/aa/full/2002/30/aa2243/Timg183.gif) |
Figure 4:
Same diagram as Figs.
 and
and
 for the groups CV5 and
CV6+CV7.
for the groups CV5 and
CV6+CV7. |
In order to again avoid the bias described by Smith & Eichhorn (1996), we introduce
now the coefficient
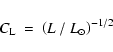 |
(12) |
from luminosity in solar units. We used the coefficient
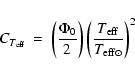 |
(13) |
in Paper I (Eq. 36). Substituting Eq. (5), we obtain
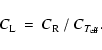 |
(14) |
From Eq. (43) of Paper I, viz.
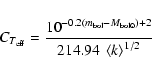 |
(15) |
and the above Eq. (5), we finally transform Eq. (12) into
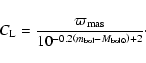 |
(16) |
This latter relation shows that
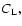 like
like
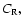 is a linear and homogeneous
function of the true parallax
is a linear and homogeneous
function of the true parallax 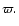 Thus it can be averaged without being affected by the
above-mentioned bias. The coefficient can be calculated from Eq. (16) with
Eq. (14) used as a checking relation. We adopted
Thus it can be averaged without being affected by the
above-mentioned bias. The coefficient can be calculated from Eq. (16) with
Eq. (14) used as a checking relation. We adopted
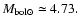 The coefficients thus obtained can be averaged and estimates of mean luminosities derived
from Eq. (12) for a group or class of carbon giants. Finally we adopt mean bolometric
luminosities as obtained from
The coefficients thus obtained can be averaged and estimates of mean luminosities derived
from Eq. (12) for a group or class of carbon giants. Finally we adopt mean bolometric
luminosities as obtained from
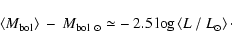 |
(17) |
Individual values of
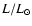 can be derived from Eqs. (16) and (12) i.e. from individual
values of the
can be derived from Eqs. (16) and (12) i.e. from individual
values of the 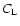 coefficients. They should not be averaged due to the mentioned bias.
The same statement applies to individual absolute bolometric magnitudes.
We shall use the latter to locate every carbon star in the HR diagram (see Sect. 7).
coefficients. They should not be averaged due to the mentioned bias.
The same statement applies to individual absolute bolometric magnitudes.
We shall use the latter to locate every carbon star in the HR diagram (see Sect. 7).
The values of 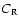 and
and 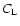 were calculated for about 300 HIPPARCOS carbon stars
with usable astrometric data. The corresponding values of
were calculated for about 300 HIPPARCOS carbon stars
with usable astrometric data. The corresponding values of
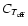 from Paper I were
completed with the 81 additional stars of Sect. 2.2. Unfortunately, a few stars from initial
proposals were missed.
In addition to C3236 = SS Vir and C5496 = RX Peg, which were not correctly inserted in the
entry catalogue (INCA), erroneous identifications affected C1616 = BK CMi, C1787 = BE CMi,
C3614 = NSV7110, C4241 = U Lyr, C5371 = LU Cep and C5970 = V532 Cas. In addition HIC 22767 is
not C808 = IRAS 04505+2241. No astrometric solution
is given for C5721 = V363 Lac, and SU Tau = HD247925, a RCB variable, was replaced by HD247901.
from Paper I were
completed with the 81 additional stars of Sect. 2.2. Unfortunately, a few stars from initial
proposals were missed.
In addition to C3236 = SS Vir and C5496 = RX Peg, which were not correctly inserted in the
entry catalogue (INCA), erroneous identifications affected C1616 = BK CMi, C1787 = BE CMi,
C3614 = NSV7110, C4241 = U Lyr, C5371 = LU Cep and C5970 = V532 Cas. In addition HIC 22767 is
not C808 = IRAS 04505+2241. No astrometric solution
is given for C5721 = V363 Lac, and SU Tau = HD247925, a RCB variable, was replaced by HD247901.
The values of 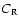 were calculated from Eq. (5), making use of
true parallaxes
were calculated from Eq. (5), making use of
true parallaxes 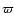 derived from HIPPARCOS observations, and the mean
relative angular diameter
derived from HIPPARCOS observations, and the mean
relative angular diameter
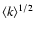 from multicolor photometry (see Sect. 3).
The parallaxes were then used in Eq. (16) together with apparent bolometric magnitudes
from multicolor photometry (see Sect. 3).
The parallaxes were then used in Eq. (16) together with apparent bolometric magnitudes
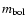 from Paper I, assuming
from Paper I, assuming
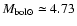 (see Sect. 5). Individual
radii and luminosities were also derived as described at the ends of Sects. 3.1 and 3.3. The
deduced individual absolute bolometric magnitudes are quoted in Table 2, which is only available
at CDS.
This table is a modified, augmented and updated version of Table 10 of Paper I available at CDS.
It contains 508 entries corresponding to 508 analyzed SEDs. Effective temperatures, interstellar
(and eventually circumstellar) extinctions, classification in our photometric groups, bolometric
magnitudes and comments are quoted there. For about 370 objects, absolute bolometric magnitudes
are given as derived from true parallaxes.
(see Sect. 5). Individual
radii and luminosities were also derived as described at the ends of Sects. 3.1 and 3.3. The
deduced individual absolute bolometric magnitudes are quoted in Table 2, which is only available
at CDS.
This table is a modified, augmented and updated version of Table 10 of Paper I available at CDS.
It contains 508 entries corresponding to 508 analyzed SEDs. Effective temperatures, interstellar
(and eventually circumstellar) extinctions, classification in our photometric groups, bolometric
magnitudes and comments are quoted there. For about 370 objects, absolute bolometric magnitudes
are given as derived from true parallaxes.


Up: Carbon-rich giants in the function
Copyright ESO 2002
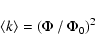
![]() -coefficient is a mean value over the wavelengths used, that is derived directly
from photometry (Knapik et al. 1999, Sect. 2.4). It is thus an angular diameter on a
relative scale as confirmed in Paper I (Sect. 8). It correlates with astrometric data, namely
estimated true parallaxes
-coefficient is a mean value over the wavelengths used, that is derived directly
from photometry (Knapik et al. 1999, Sect. 2.4). It is thus an angular diameter on a
relative scale as confirmed in Paper I (Sect. 8). It correlates with astrometric data, namely
estimated true parallaxes ![]() from Knapik et al. (1998; Sect. 4), in the expected
way. The reference angular diameters
from Knapik et al. (1998; Sect. 4), in the expected
way. The reference angular diameters ![]() were calibrated as a function of effective
temperatures (Paper I, Sect. 11), viz.
were calibrated as a function of effective
temperatures (Paper I, Sect. 11), viz.
![]() .
The coefficient may
still be written as
.
The coefficient may
still be written as
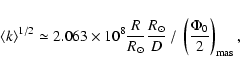
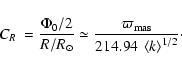
![]() may be derived from individual
may be derived from individual ![]() 's as quoted
in Paper I or from
's as quoted
in Paper I or from
![]() relations, to be replaced in Eq. (5).
They should not be averaged since the corresponding means could be biased.
relations, to be replaced in Eq. (5).
They should not be averaged since the corresponding means could be biased.
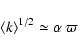
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{fi2.eps} \end{figure}](/articles/aa/full/2002/30/aa2243/Timg139.gif)
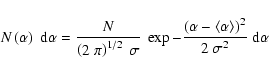
![\begin{displaymath}N\left(\alpha\right)~\rm {d} \alpha \simeq 6.050 \: \exp \left[ -156~\left(\alpha - 0.148
\right)^{2}\right]\;\rm {d}\alpha.
\end{displaymath}](/articles/aa/full/2002/30/aa2243/img168.gif)
![]() for the sequence of groups in our
classification. They roughly correspond to inferior and superior limits in relative
radii
for the sequence of groups in our
classification. They roughly correspond to inferior and superior limits in relative
radii
![]() for a given range in
for a given range in ![]() A general increase of both limits is
noticed along the sequence of photometric groups which is moderate till HC3 and then from
CV3 to CV6, where steady extremas at nearly
A general increase of both limits is
noticed along the sequence of photometric groups which is moderate till HC3 and then from
CV3 to CV6, where steady extremas at nearly
![]() and
and
![]() are reached.
Such flattenings at both ends of the sequence will be found again while deriving
luminosities and studying the locus of carbon giants in the HR diagram (Sects. 5 to 7).
are reached.
Such flattenings at both ends of the sequence will be found again while deriving
luminosities and studying the locus of carbon giants in the HR diagram (Sects. 5 to 7).
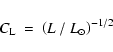
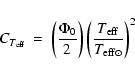
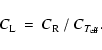
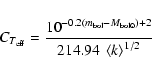
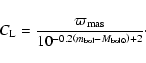
![]() and
and ![]() were calculated for about 300 HIPPARCOS carbon stars
with usable astrometric data. The corresponding values of
were calculated for about 300 HIPPARCOS carbon stars
with usable astrometric data. The corresponding values of
![]() from Paper I were
completed with the 81 additional stars of Sect. 2.2. Unfortunately, a few stars from initial
proposals were missed.
In addition to C3236 = SS Vir and C5496 = RX Peg, which were not correctly inserted in the
entry catalogue (INCA), erroneous identifications affected C1616 = BK CMi, C1787 = BE CMi,
C3614 = NSV7110, C4241 = U Lyr, C5371 = LU Cep and C5970 = V532 Cas. In addition HIC 22767 is
not C808 = IRAS 04505+2241. No astrometric solution
is given for C5721 = V363 Lac, and SU Tau = HD247925, a RCB variable, was replaced by HD247901.
from Paper I were
completed with the 81 additional stars of Sect. 2.2. Unfortunately, a few stars from initial
proposals were missed.
In addition to C3236 = SS Vir and C5496 = RX Peg, which were not correctly inserted in the
entry catalogue (INCA), erroneous identifications affected C1616 = BK CMi, C1787 = BE CMi,
C3614 = NSV7110, C4241 = U Lyr, C5371 = LU Cep and C5970 = V532 Cas. In addition HIC 22767 is
not C808 = IRAS 04505+2241. No astrometric solution
is given for C5721 = V363 Lac, and SU Tau = HD247925, a RCB variable, was replaced by HD247901.
![]() were calculated from Eq. (5), making use of
true parallaxes
were calculated from Eq. (5), making use of
true parallaxes ![]() derived from HIPPARCOS observations, and the mean
relative angular diameter
derived from HIPPARCOS observations, and the mean
relative angular diameter
![]() from multicolor photometry (see Sect. 3).
The parallaxes were then used in Eq. (16) together with apparent bolometric magnitudes
from multicolor photometry (see Sect. 3).
The parallaxes were then used in Eq. (16) together with apparent bolometric magnitudes
![]() from Paper I, assuming
from Paper I, assuming
![]() (see Sect. 5). Individual
radii and luminosities were also derived as described at the ends of Sects. 3.1 and 3.3. The
deduced individual absolute bolometric magnitudes are quoted in Table 2, which is only available
at CDS.
This table is a modified, augmented and updated version of Table 10 of Paper I available at CDS.
It contains 508 entries corresponding to 508 analyzed SEDs. Effective temperatures, interstellar
(and eventually circumstellar) extinctions, classification in our photometric groups, bolometric
magnitudes and comments are quoted there. For about 370 objects, absolute bolometric magnitudes
are given as derived from true parallaxes.
(see Sect. 5). Individual
radii and luminosities were also derived as described at the ends of Sects. 3.1 and 3.3. The
deduced individual absolute bolometric magnitudes are quoted in Table 2, which is only available
at CDS.
This table is a modified, augmented and updated version of Table 10 of Paper I available at CDS.
It contains 508 entries corresponding to 508 analyzed SEDs. Effective temperatures, interstellar
(and eventually circumstellar) extinctions, classification in our photometric groups, bolometric
magnitudes and comments are quoted there. For about 370 objects, absolute bolometric magnitudes
are given as derived from true parallaxes.