The interstellar and circumstellar
extinction on the line of sight to each star is simultaneously determined, and a mean
coefficient
![]() calculated, which proved to be an angular diameter on a
relative scale for a given effective temperature (or eventually for a given photometric
group: see Paper I). The new effective temperatures proposed for carbon-rich giants and related
objects in Paper I rely on spectral energy distributions (SEDs), model atmospheres and measured
angular diameters. The classification and the homogeneous temperature scale obtained proved to
be tightly correlated. It was concluded that the main parameter of this photometric
classification is effective temperature (Paper I), which is not the case of classical spectral
classifications. Amongst the remaining parameters, the C/O
ratio has an important influence. For CV-stars, the mean values and dispersions increase along
the sequence (CV2 to CV6) of photometric groups (Paper I, Sect. 10).
calculated, which proved to be an angular diameter on a
relative scale for a given effective temperature (or eventually for a given photometric
group: see Paper I). The new effective temperatures proposed for carbon-rich giants and related
objects in Paper I rely on spectral energy distributions (SEDs), model atmospheres and measured
angular diameters. The classification and the homogeneous temperature scale obtained proved to
be tightly correlated. It was concluded that the main parameter of this photometric
classification is effective temperature (Paper I), which is not the case of classical spectral
classifications. Amongst the remaining parameters, the C/O
ratio has an important influence. For CV-stars, the mean values and dispersions increase along
the sequence (CV2 to CV6) of photometric groups (Paper I, Sect. 10).
Bergeat et al. (Paper II) analyzed the space distribution and
kinematics of Galactic carbon giants. They showed that the HC-sample (essentially early-R
stars) is a component of the thick disk contaminated by the CH stars which are a spheroidal
contribution (see also Hartwick & Cowley 1985). The HC-stars not classified as CH
stars probably correspond to old ![]()
![]() low initial-mass stars (say
low initial-mass stars (say ![]()
![]() ). It was also shown in Paper II that the CV-sample
(mainly N stars) is a component of the old (thin) disk, dated
). It was also shown in Paper II that the CV-sample
(mainly N stars) is a component of the old (thin) disk, dated
![]() on average, but with a large spread from a few
on average, but with a large spread from a few
![]() to nearly
to nearly
![]() The corresponding initial masses should range from about
The corresponding initial masses should range from about
![]() to a few solar masses.
Corrections to the (small) effects of the Malmquist bias on the HIPPARCOS sample of carbon
giants were also obtained in Paper II. They are applied hereafter to quoted mean luminosities.
to a few solar masses.
Corrections to the (small) effects of the Malmquist bias on the HIPPARCOS sample of carbon
giants were also obtained in Paper II. They are applied hereafter to quoted mean luminosities.
The calibrations were acquired from the sample of 390 stars (Paper I).
Several couples
![]() were finally selected by trial and error amongst
our data. They represent our "best choices'' on the
were finally selected by trial and error amongst
our data. They represent our "best choices'' on the
![]() to
to
![]() range. The classical CBK vs.
range. The classical CBK vs.
![]() plot is shown in Fig.
plot is shown in Fig.
![]() The earlier diagram of Frogel et al.
(1980; their Fig. 2, p. 498) is confirmed and extended at both ends.
The earlier diagram of Frogel et al.
(1980; their Fig. 2, p. 498) is confirmed and extended at both ends.
Except for about 20-30 objects, the stars populate a well-defined locus from (0.0, 0.8) to
(2.5, 3.4). The discrepant objects are located below this locus due to
thermal emission from circumstellar (CS) grains in the infrared, usually starting from the
H-bandpass at
![]() and increasing longwards.
The J-bandpass at
and increasing longwards.
The J-bandpass at
![]() is much less affected
while the K-bandpass at
is much less affected
while the K-bandpass at
![]() is much more affected. Finally the CS vector in
the diagram is oriented toward lower CBK and larger
is much more affected. Finally the CS vector in
the diagram is oriented toward lower CBK and larger
![]() as seen in
Fig.
as seen in
Fig.
![]() The extreme ("infrared'') carbon stars such as
The extreme ("infrared'') carbon stars such as
![]() Leo
and
Leo
and
![]() ,
are so strongly shifted that they fall outside the frame. In this diagram,
the Ba II stars do not differ appreciably from the hot carbon (HC) stars, which allows one
to adopt the same mean relation. With the exception of a few stars,
the RCB variables do exhibit a substantial IR excess. They populate a strip located well
below the relation for carbon and Ba II stars. This is also the case of C2011, a star with
a silicate-type IR excess. In such cases the CBK vs.
,
are so strongly shifted that they fall outside the frame. In this diagram,
the Ba II stars do not differ appreciably from the hot carbon (HC) stars, which allows one
to adopt the same mean relation. With the exception of a few stars,
the RCB variables do exhibit a substantial IR excess. They populate a strip located well
below the relation for carbon and Ba II stars. This is also the case of C2011, a star with
a silicate-type IR excess. In such cases the CBK vs.
![]() couple
cannot be used to estimate bolometric corrections. For
couple
cannot be used to estimate bolometric corrections. For
![]() that
is dealing with carbon variables of the CV6-CV7 groups, the proportion of stars with an
appreciable IR excess increases. The locus widens in a leek-shaped structure for increasing
color indices. Following a wide maximum, a decrease of the bolometric correction is observed for
increasing indices. Here again, the mean relation cannot safely be used. Thus, we calibrated
data at shorter wavelengths. The assumption of constant total radiated power when absorbed light
is re-radiated in the IR by CS grains deserves discussion, depending on shell geometry and/or
dust properties. Bergeat et al. (2002, Paper I, Sect. 13) found that for a few hot carbon (HC) stars
and RCB variables, corrections need to be applied due to non-spherical symmetry. On the contrary,
they estimated that reasonable values can be obtained from dereddened SEDs without IR excesses
or from observed SEDs including IR excesses in the case of cool carbon variables (CV6-CV7) with
strong thermal emission.
that
is dealing with carbon variables of the CV6-CV7 groups, the proportion of stars with an
appreciable IR excess increases. The locus widens in a leek-shaped structure for increasing
color indices. Following a wide maximum, a decrease of the bolometric correction is observed for
increasing indices. Here again, the mean relation cannot safely be used. Thus, we calibrated
data at shorter wavelengths. The assumption of constant total radiated power when absorbed light
is re-radiated in the IR by CS grains deserves discussion, depending on shell geometry and/or
dust properties. Bergeat et al. (2002, Paper I, Sect. 13) found that for a few hot carbon (HC) stars
and RCB variables, corrections need to be applied due to non-spherical symmetry. On the contrary,
they estimated that reasonable values can be obtained from dereddened SEDs without IR excesses
or from observed SEDs including IR excesses in the case of cool carbon variables (CV6-CV7) with
strong thermal emission.
Finally, we made use of eight
![]() vs. IC0 mean
relations, namely
vs. IC0 mean
relations, namely
![]()
![]() CBH and
CBK vs.
CBH and
CBK vs.
![]() CBH and
CBK vs.
CBH and
CBK vs.
![]() and finally CBHand CBK vs.
and finally CBHand CBK vs.
![]() The magnitudes
The magnitudes
![]() and
and
![]() are such as defined by Knapik & Bergeat (1997) from the
data obtained in narrow bandpasses by Baumert (1972). The adopted mean relations
are given in Appendix. Departures between values deduced from short wavelengths on one hand
and from long
wavelengths on the other hand, if any, are estimated to be less than 0.1 mag. Finally, the
estimates are averaged and the errors on the resulting bolometric correction should not
exceed 0.05 mag for the 81 carbon stars studied in this way. The absolute bolometric
magnitudes in forthcoming sections are of course affected, but the effect can
be neglected when true luminosity dispersions and uncertainties on true parallaxes are
taken into account.
are such as defined by Knapik & Bergeat (1997) from the
data obtained in narrow bandpasses by Baumert (1972). The adopted mean relations
are given in Appendix. Departures between values deduced from short wavelengths on one hand
and from long
wavelengths on the other hand, if any, are estimated to be less than 0.1 mag. Finally, the
estimates are averaged and the errors on the resulting bolometric correction should not
exceed 0.05 mag for the 81 carbon stars studied in this way. The absolute bolometric
magnitudes in forthcoming sections are of course affected, but the effect can
be neglected when true luminosity dispersions and uncertainties on true parallaxes are
taken into account.
The Malmquist bias (1924, 1936) affects any sample delineated on the
grounds of a limited apparent magnitude. We found
![]() for the HIPPARCOS
sample of carbon stars (Knapik et al. 1998), refined as
for the HIPPARCOS
sample of carbon stars (Knapik et al. 1998), refined as
![]() for the HC-stars and
for the HC-stars and
![]() for the CV-stars (Paper II). Mean absolute
magnitudes are found too bright since increasing selection occurs amongst more and more distant
stars, favoring the intrinsically brighter objects. In Sect. 4 of Paper II, corrections to
mean absolute bolometric magnitudes were derived which amounted to a few tenths of a magnitude
at most (+0.32 mag at HC1 and +0.2 mag at HC2 are the largest values, against 0.1 mag or less
for the other groups). A second aspect is the
increasing deficits at increasing distances from Sun, in stellar number densities (the missing
objects in Fig. 1 of Paper II) and in stellar surface densities as projected on the Plane
(Sect. 5.1 of Paper II). This latter effect lowers the q-exponent of the HIPPARCOS distribution
of true (as opposed to observed) parallaxes
for the CV-stars (Paper II). Mean absolute
magnitudes are found too bright since increasing selection occurs amongst more and more distant
stars, favoring the intrinsically brighter objects. In Sect. 4 of Paper II, corrections to
mean absolute bolometric magnitudes were derived which amounted to a few tenths of a magnitude
at most (+0.32 mag at HC1 and +0.2 mag at HC2 are the largest values, against 0.1 mag or less
for the other groups). A second aspect is the
increasing deficits at increasing distances from Sun, in stellar number densities (the missing
objects in Fig. 1 of Paper II) and in stellar surface densities as projected on the Plane
(Sect. 5.1 of Paper II). This latter effect lowers the q-exponent of the HIPPARCOS distribution
of true (as opposed to observed) parallaxes
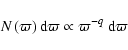 |
(1) |
The bias studied by Smith & Eichhorn (1996) occurs every time a mean value is
calculated for a quantity which is not a linear function of true parallaxes. Even if the
distribution according to true parallaxes is a Gaussian, that of distances or absolute
magnitudes is not. Smith & Eichhorn derived the mathematical expectation of distances from
parallaxes affected by arbitrarily high errors (![]() ,
their Fig. 1, p. 213). An overestimate
is found for
,
their Fig. 1, p. 213). An overestimate
is found for
![]() which changes into an underestimate for
which changes into an underestimate for
![]() The consequence of this effect and the methods used to avoid it in various
circumstances can be found
in Bergeat et al. (1998), Knapik et al. (1998), Sects. 3.1 and 3.2 of
Paper II, Sects. 3.1 and 3.3 of Paper III, and in Sect. 2.1 of the present paper.
The consequence of this effect and the methods used to avoid it in various
circumstances can be found
in Bergeat et al. (1998), Knapik et al. (1998), Sects. 3.1 and 3.2 of
Paper II, Sects. 3.1 and 3.3 of Paper III, and in Sect. 2.1 of the present paper.
The third bias results from the effect of errors on a distribution non-uniform in parallaxes.
Let us assume that the probability distribution function (pdf) of repeated individual
observations of a single true parallax
![]() is a Gaussian centered on the
is a Gaussian centered on the
![]() -value, with
-value, with ![]() as a standard deviation. Now we consider an other problem which
is to derive the pdf of true parallaxes
as a standard deviation. Now we consider an other problem which
is to derive the pdf of true parallaxes
![]() for a given sample of stars
whose observed parallaxes are the
for a given sample of stars
whose observed parallaxes are the
![]() 's from the HIPPARCOS catalogue. This pdf is
the same Gaussian as mentioned above, provided the stars are uniformly distributed in true
parallaxes
(Lutz & Kelker 1973). This latter condition is completely unrealistic and Lutz
& Kelker adopted a uniform space density in their pioneering work, that is
's from the HIPPARCOS catalogue. This pdf is
the same Gaussian as mentioned above, provided the stars are uniformly distributed in true
parallaxes
(Lutz & Kelker 1973). This latter condition is completely unrealistic and Lutz
& Kelker adopted a uniform space density in their pioneering work, that is
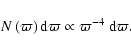 |
(2) |
It is interesting to note that future astrometric missions like GAIA (ESA 1995) will be almost free from those biases, due to their very high accuracies and extensive sampling, reaching the edges of the galactic disk. The main difficulty will then result from non-uniform brightness distributions on extended stellar discs.
Copyright ESO 2002