

Up: The carrier of the stars
3 Continuum
a Temperature determination uncertain due to optically thick MgS emission.
In order to extract the profiles of the "30'' 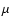 m features and
compare them from source to source, we model the underlying continuum
due to the emission of other circumstellar (CS) dust components.
First, we present the way we construct these continua and in
Sect. 4, we discuss the resulting profiles.
m features and
compare them from source to source, we model the underlying continuum
due to the emission of other circumstellar (CS) dust components.
First, we present the way we construct these continua and in
Sect. 4, we discuss the resulting profiles.
To model the underlying continuum we use a simplified approach. We
represent the continuum with a single temperature modified blackbody,
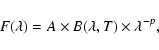 |
(1) |
where 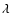 is the wavelength,
is the wavelength,
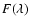 is the flux density of
the continuum,
is the flux density of
the continuum,
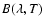 is the Planck function of temperature
T, p is the dust emissivity index and A is a scaling factor.
is the Planck function of temperature
T, p is the dust emissivity index and A is a scaling factor.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3527f05.eps} \end{figure}](/articles/aa/full/2002/29/aah3527/Timg27.gif) |
Figure 5:
Examples of the fitted continuum. We show the spectra
(black line), the selected continuum points (diamonds) and the
fitted modified blackbody (grey line). |
We have chosen this approach to estimate the continuum over doing a
radiative transfer calculation for reasons of simplicity. The bulk of
the CS dust around these sources consists of some form of amorphous
carbon grains that do not exhibit sharp emission features in the
wavelength range of interest. Therefore, a radiative transfer
calculation will not yield extra insight into the shape or strength of
the continuum while introducing many more modelling parameters. This
method has the advantage that we can compare the feature in such a
diverse group of sources in a consistent way. Of course
Eq. (1) does not directly allow us to
incorporate important effects such as optical depth or temperature
gradients. However varying the p-parameter can mimic these effects
to some extent.
The p-parameter reflects the efficiency with which the dust grains
can emit at wavelengths larger than the grain size. Reasonable values
of p in the region of interest are between 1 and 2. Crystalline
materials have this value close to 2 and amorphous materials have a
p-value between 1 and 2, while layered materials have an emissivity
index close to 1. A temperature gradient in the dust shell will result
in a broader spectral energy distribution (SED). This is mimicked by a
lower value of p. Likewise an optically thick dust shell will result
in a broader SED, which again can be reproduced by reducing the value of p.
We use a
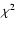 fitting procedure to determine the values of Tand p fitted to selected continuum points in the ranges 2-22
fitting procedure to determine the values of Tand p fitted to selected continuum points in the ranges 2-22 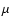 m. If available we also use the LWS spectra to verify the
continuum at the long wavelength end of the "30''
m. If available we also use the LWS spectra to verify the
continuum at the long wavelength end of the "30'' 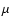 m feature.
The 50-100
m feature.
The 50-100 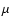 m continuum gives an even stronger
constraint on the value of p. For most cases the resultant
continuum runs through the 45
m continuum gives an even stronger
constraint on the value of p. For most cases the resultant
continuum runs through the 45 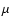 m region of the SWS spectrum. A
remarkable exception to this is the spectrum of RAFGL 3068. The
2-24
m region of the SWS spectrum. A
remarkable exception to this is the spectrum of RAFGL 3068. The
2-24 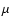 m spectrum is well fitted with a single 290 K Planck function.
However we find a large excess of this continuum at 45
m spectrum is well fitted with a single 290 K Planck function.
However we find a large excess of this continuum at 45 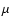 m and the
available LWS spectrum is not well represented in level or slope.
Possibly this is due to the optically thick dust shell or a biaxial
dust/temperature distribution.
m and the
available LWS spectrum is not well represented in level or slope.
Possibly this is due to the optically thick dust shell or a biaxial
dust/temperature distribution.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3527f06.eps} \end{figure}](/articles/aa/full/2002/29/aah3527/Timg29.gif) |
Figure 6:
Centroid of the "30'' 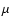 m feature with respect to the
[25]-[60] colour. The symbols are like in
Fig. 1. There is a clear trend for the
centroid position of the "30'' m feature with respect to the
[25]-[60] colour. The symbols are like in
Fig. 1. There is a clear trend for the
centroid position of the "30'' 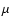 m feature to move to longer
wavelengths the redder the object is. m feature to move to longer
wavelengths the redder the object is. |
The values for T and p are listed in Table 2.
One remarkable fact is that the C-stars are well fitted by a single
temperature Planck function over the complete wavelength range of SWS.
The IR SEDs of the post-AGBs and PNe are in general less broad and
many sources are better fitted with a p-value of 1. We stress
however that the derived p values cannot be used to constrain the
crystal structure or the average size of the dust grains in view of
the aforementioned effects of temperature gradients and optical depth.


Up: The carrier of the stars
Copyright ESO 2002
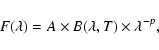
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3527f05.eps} \end{figure}](/articles/aa/full/2002/29/aah3527/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3527f06.eps} \end{figure}](/articles/aa/full/2002/29/aah3527/Timg29.gif)