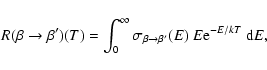3 Calculated and fitted collisional rates

The state-to-state rotational inelastic rates are the Boltzmann thermal averages of the state-to-state inelastic cross sections:

$$R(\beta \rightarrow \beta')(T) = \int_0^{\infty} \sigma _{\beta\rightarrow \beta'}(E)~E {\rm e}^{-E/kT}~ {\rm d}E,$$ (1)

where $\beta\equiv j\alpha,j_2$ and $\beta'\equiv j'\alpha',j'_2$, unprimed and primed quantum numbers label initial and final states of the molecules, j and j₂ are the rotational angular momenta of H₂O and H₂, and $\alpha$ specifies the other H₂O quantum numbers (e.g. K_-1, K₁). The rates are obtained using a Simpson rule for temperatures ranging from 5 K to 20 K. Calculations are made over essentially the whole energy range spanned by the Boltzmann distributions; the highest energy point calculated is at the threshold energy of the transition plus 10 kT.

We perform CC calculations with a B(j, 2) basis set in the energy range from the opening of the lowest inelastic channel to 381 cm^-1 for ortho H₂O, and to 380 cm^-1 for para H₂O. The energies are total energies. We use a B(j, 4) basis set and CS calculations above the energy threshold of the opening of the j₂ =2 rotational level of H₂. We carefully spanned the energy ranges above the inelastic channels and we added more points in presence of broad resonance structures. For ortho water the energy step is 0.1 cm^-1 below 97 cm^-1, 0.1, 0.2 or 0.5 cm^-1 in an energy range of 20 cm^-1 above each inelastic threshold, and small but irregular in the other energy ranges. For para water the energy step is 0.1 cm^-1 from 37.2 cm^-1 to 75.2 cm^-1, 0.2 cm^-1 from 75.2 cm^-1 to 80 cm^-1, 1 cm^-1 between 80 cm^-1 and 175 cm^-1 (with some additional points every 0.2 cm^-1 or 0.5 cm^-1) and 1 cm^-1 or 5 cm^-1 above 175 cm^-1.

For a collision of H₂O with para-H₂ Phillips et al. (1995) pointed out that it is necessary to use a B(j, 2) basis set instead of a B(j, 0) basis set in the temperature range from 20 K to 140 K. This is still important at very low temperature; we find a relative difference of 31% at T=8 K and of 22% at T=20 K between the collision rates $R(1_{0,1}\rightarrow 1_{1,0})$ calculated respectively with a B(5, 2) and a B(5, 0) basis set. The j₂=2 channel of H₂ has a strong influence on the resonance structure at low energy. As an example, Fig. 2 shows the change in the resonance structure of the CC $1_{0,1}\rightarrow 1_{1,0}$ cross section calculated with and without the j₂=2 channel of H₂.

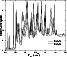Figure 2: Resonance structures of the CC $1_{0,1}\rightarrow 1_{1,0}$ cross sections calculated with the B(5, 0) basis set (dashed line) and with the B(5, 2)basis set (solid line). Cross sections are in Å2.

The presence of overlapping resonances necessitates the use of a very fine grid of energy points in the thermal Boltzmann average (Eq. (1)) in order to correctly reproduce the resonance structure. This is illustrated in Fig. 3 for the transition $(1_{0,1}\rightarrow 1_{1,0})$, showing that the collision rate $R(1_{0,1},j_2=0\rightarrow 1_{1,0},j_2'=0)$ varies significantly and randomly with respect to small changes in the energy step size. Our best integrals are done by a Simpson rule using integration energy points which follow the calculated cross sections. Our low-energy step size of 0.1 cm^-1 is particularly small; other published results (Phillips et al. 1996) at 20 K are usually obtained with sparser energy grids because of the computing time required.

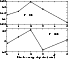Figure 3: Inelastic rate constants (in cm3 s-1) of the $1_{0,1}\rightarrow 1_{1,0}$transition versus the energy step size in cm-1 at T=8 K and T=20 K.

Another issue is the use of CS calculations in the highest energy range. The CS calculations are relatively accurate for the lowest rotational transitions, but are particularly inaccurate for the largest rotational transitions. Nevertheless the ratio between CC calculations and CS calculations is roughly constant at energies between 328 cm^-1 and 381 cm^-1, and we use this ratio to scale our CS calculations above 388 cm^-1.

Finally we investigate the addition of the j₂=4 channel for calculations at energies higher that the opening of the j₂=2 channel. The overall effect is negligible at the temperatures considered here.

Tables 3 and 4 give the effective rotational inelastic rates for ortho and para H₂O respectively, together with the values obtained by Phillips et al. (1996) at 20 K. These effective rotational inelastic rates correspond to the sum of the inelastic rates (Eq. (1)) over the final j₂' states for a given initial j₂:

$$\hat{R}_{j_2=0}(j\alpha \rightarrow j'\alpha')(T) = \sum_{j'_2} R(j\alpha, j_2=0 \rightarrow j'\alpha', j'_2)(T).$$ (2)

In the temperature range between 5 K and 20 K, the inelastic rates from transitions between j₂=0 and j'₂=2 are totally negligible.

We believe that the discrepancies between our rates and the Phillips et al. (1996) rates at 20 K are mainly due to the sparser energy grid used by those authors and that our rate coefficients have an overall accuracy of 3% minimum for all given transitions and temperatures.

For astrophysical use, all our effective excitation rates may be fitted by the analytical form used by Balakrishnan et al. (1999):

$$\log_{10} \hat{R}_{j_2=0}(j\alpha \rightarrow j'\alpha') (T) ... ..._{n=0}^{N} a^{(n)}_{j_2=0;j\alpha \rightarrow j'\alpha'}~~ x^n$$ (3)

where x = 1/T^1/3. Tables 5 and 6 give the values of $a_{j_2=0;j\alpha \rightarrow j'\alpha'}$ for the effective rate coefficients given in Tables 3 and 4 respectively. A fourth-order polynomial is required to cover the whole range of temperature and to provide a fitting error better than 0.02% on all rate coefficients. We emphasize that these fits are only valid in the temperature range from 5 K to 20 K.

This fitted functions are very different from the function sometimes used by astrophysicists, when no data are available:

$$R(x\rightarrow x')(T) = R(x\rightarrow x')(T=T_0) {\left( {\frac{T}{T_0}}\right)^{1/2}}\cdot$$ (4)

For example, Fig. 4 shows the large difference at low temperature between our calculated rates and the function of Eq. (4) with T₀=20 K, for the transition $1_{0,1}\rightarrow 1_{1,0}$.

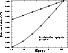Figure 4: Comparison between the effective calculated CC rates (Eq. (2)) and the rates obtained with Eq. (4), for the transition $1_{0,1}\rightarrow 1_{1,0}$.

Moreover the deexcitation rate of the $2_{2,1}\rightarrow 2_{1,2}$ transition increases when the temperature decreases, and the deexcitation rates from the 3_0,3 level increase and then decrease again when the temperature decreases. It is therefore not justified to use this simple approximation at very low temperature.

 

 

Table 3: Effective excitation rates of Eq. (2) (in cm³ s^-1) of ortho-H₂O with para-H₂. The levels are labelled with j_K-1K1. The column "Points'' gives the number of energy points used in the Boltzmann average. The last column gives the data of Phillips et al. (1996).

Initial	Final	Points	5	8	12	16	20	20
10,1	11,0	1033	3.92(-14)	4.34(-13)	1.71(-12)	3.36(-12)	4.99(-12)	3.06(-12)
10,1	21,2	680	3.69(-18)	1.54(-15)	4.41(-14)	2.37(-13)	6.52(-13)	6.10(-13)
10,1	22,1	441	7.74(-26)	1.35(-20)	1.12(-17)	3.25(-16)	2.46(-15)	2.42(-15)
10,1	30,3	424	1.42(-25)	2.89(-20)	2.60(-17)	7.82(-16)	6.04(-15)	5.88(-15)
10,1	31,2	353	1.86(-31)	2.03(-24)	1.70(-20)	1.56(-18)	2.34(-17)	2.26(-17)
10,1	32,1	272	4.73(-36)	3.30(-27)	2.74(-22)	7.95(-20)	2.40(-18)	1.74(-18)
10,1	33,0	92	4.03(-46)	7.54(-34)	4.95(-27)	1.26(-23)	1.40(-21)	8.57(-22)
10,1	41,4	211	8.56(-37)	2.23(-27)	3.81(-22)	1.57(-19)	5.78(-18)	5.98(-18)
10,1	42,3	62	1.00(-47)	9.20(-35)	1.47(-27)	5.91(-24)	8.61(-22)	8.05(-22)
11,0	10,1	1033	8.22(-12)	1.23(-11)	1.58(-11)	1.78(-11)	1.90(-11)	1.17(-11)
11,0	21,2	680	6.10(-16)	3.56(-14)	3.44(-13)	1.07(-12)	2.10(-12)	1.94(-12)
11,0	22,1	441	9.16(-23)	2.05(-18)	5.36(-16)	8.60(-15)	4.53(-14)	4.44(-14)
11,0	30,3	424	1.37(-23)	3.72(-19)	1.07(-16)	1.80(-15)	9.73(-15)	9.90(-15)
11,0	31,2	353	4.17(-28)	6.06(-22)	1.64(-18)	8.56(-17)	9.23(-16)	8.63(-16)
11,0	32,1	272	3.32(-34)	3.10(-26)	8.42(-22)	1.40(-19)	3.06(-18)	2.56(-18)
11,0	33,0	92	4.30(-43)	1.05(-31)	2.17(-25)	3.10(-22)	2.42(-20)	2.45(-20)
11,0	41,4	211	1.74(-35)	6.07(-27)	3.40(-22)	8.07(-20)	2.16(-18)	2.12(-18)
11,0	42,3	62	1.93(-44)	2.37(-32)	1.25(-25)	2.87(-22)	3.00(-20)	2.57(-20)
21,2	10,1	680	2.03(-11)	2.07(-11)	2.10(-11)	2.13(-11)	2.15(-11)	2.02(-11)
21,2	11,0	680	1.60(-11)	1.69(-11)	1.77(-11)	1.81(-11)	1.82(-11)	1.68(-11)
21,2	22,1	441	1.22(-18)	4.71(-16)	1.30(-14)	6.81(-14)	1.84(-13)	1.64(-13)
21,2	30,3	424	1.95(-18)	9.56(-16)	2.97(-14)	1.64(-13)	4.51(-13)	5.01(-13)
21,2	31,2	353	4.45(-23)	1.22(-18)	3.60(-16)	6.20(-15)	3.41(-14)	3.12(-14)
21,2	32,1	272	3.08(-28)	5.19(-22)	1.50(-18)	8.04(-17)	8.77(-16)	8.95(-16)
21,2	33,0	92	1.08(-38)	5.00(-29)	1.17(-23)	5.67(-21)	2.32(-19)	2.08(-19)
21,2	41,4	211	4.22(-30)	2.79(-23)	1.74(-19)	1.38(-17)	1.92(-16)	1.42(-16)
21,2	42,3	62	2.82(-40)	6.42(-30)	3.64(-24)	2.73(-21)	1.44(-19)	1.20(-19)
22,1	10,1	441	3.56(-12)	3.87(-12)	4.11(-12)	4.26(-12)	4.37(-12)	4.32(-12)
22,1	11,0	441	2.01(-11)	2.08(-11)	2.11(-11)	2.12(-11)	2.11(-11)	2.08(-11)
22,1	21,2	441	1.03(-11)	1.00(-11)	9.97(-12)	9.93(-12)	9.89(-12)	8.84(-12)
22,1	30,3	424	1.50(-12)	2.13(-12)	2.66(-12)	2.95(-12)	3.08(-12)	2.76(-12)
22,1	31,2	353	1.62(-16)	1.31(-14)	1.53(-13)	5.12(-13)	1.04(-12)	8.43(-13)
22,1	32,1	272	6.50(-21)	2.96(-17)	3.23(-15)	3.37(-14)	1.38(-13)	1.06(-13)
22,1	33,0	92	4.41(-30)	5.11(-23)	4.28(-19)	3.89(-17)	5.83(-16)	5.77(-16)
22,1	41,4	211	1.15(-23)	1.89(-19)	4.20(-17)	6.31(-16)	3.23(-15)	3.84(-15)
22,1	42,3	62	4.72(-33)	2.83(-25)	6.08(-21)	9.03(-19)	1.84(-17)	1.16(-17)
30,3	10,1	424	8.02(-12)	8.30(-12)	8.54(-12)	8.67(-12)	8.76(-12)	8.56(-12)
30,3	11,0	424	3.70(-12)	3.77(-12)	3.79(-12)	3.75(-12)	3.71(-12)	3.79(-12)
30,3	21,2	424	2.01(-11)	2.04(-11)	2.04(-11)	2.02(-11)	1.99(-11)	2.21(-12)
30,3	22,1	424	1.84(-12)	2.14(-12)	2.38(-12)	2.49(-12)	2.52(-12)	2.26(-12)
30,3	31,2	353	3.12(-16)	1.71(-14)	1.60(-13)	4.88(-13)	9.54(-13)	1.02(-12)
30,3	32,1	272	1.08(-21)	4.11(-18)	3.97(-16)	3.85(-15)	1.49(-14)	1.10(-14)
30,3	33,0	92	2.50(-31)	2.34(-24)	1.72(-20)	1.46(-18)	2.08(-17)	1.87(-17)
30,3	41,4	211	4.18(-22)	5.63(-18)	1.11(-15)	1.54(-14)	7.41(-14)	6.94(-14)
30,3	42,3	62	9.24(-33)	4.60(-25)	8.88(-21)	1.25(-18)	2.46(-17)	1.89(-17)

 

 

Table 4: Effective excitation rates of Eq. (2) (in cm³ s^-1) of para-H₂O with para-H₂. The levels are labelled with j_K-1K1. The column "Points'' gives the number of energy points used in the Boltzmann average. The last column gives the data of Phillips et al. (1996).

Initial	Final	Points	5	8	12	16	20	20
00,0	11,1	642	8.47(-16)	5.37(-14)	5.26(-13)	1.62(-12)	3.17(-12)	3.17(-12)
00,0	20,2	313	1.24(-19)	2.51(-16)	1.74(-14)	1.45(-13)	5.16(-13)	4.72(-13)
00,0	21,1	208	3.30(-25)	1.96(-20)	9.95(-18)	2.24(-16)	1.42(-15)	8.42(-16)
00,0	22,0	141	5.96(-29)	1.56(-22)	5.72(-19)	3.47(-17)	4.09(-16)	2.99(-16)
00,0	31,3	123	3.14(-29)	1.47(-22)	7.47(-19)	5.28(-17)	6.75(-16)	6.97(-16)
00,0	32,2	83	1.89(-40)	9.58(-31)	2.46(-25)	1.29(-22)	5.76(-21)	4.78(-21)
00,0	40,4	72	2.94(-40)	7.27(-30)	4.33(-24)	3.35(-21)	1.82(-19)	1.54(-19)
00,0	41,3	54	1.08(-48)	1.73(-35)	3.92(-28)	1.82(-24)	2.79(-22)	9.74(-34)
00,0	33,1	44	4.90(-49)	1.38(-35)	4.03(-28)	2.15(-24)	3.66(-22)	2.71(-22)
11,1	00,0	642	1.24(-11)	1.42(-11)	1.51(-11)	1.53(-11)	1.53(-11)	1.53(-11)
11,1	20,2	313	2.71(-15)	8.35(-14)	5.54(-13)	1.41(-12)	2.45(-12)	1.55(-12)
11,1	21,1	208	4.29(-18)	2.42(-15)	8.35(-14)	4.92(-13)	1.42(-12)	1.33(-12)
11,1	22,0	141	1.16(-23)	5.19(-19)	1.97(-16)	3.80(-15)	2.23(-14)	2.43(-14)
11,1	31,3	123	8.74(-25)	7.88(-20)	4.55(-17)	1.10(-15)	7.47(-15)	7.01(-15)
11,1	32,2	83	2.71(-33)	2.46(-25)	6.57(-21)	1.07(-18)	2.26(-17)	2.12(-17)
11,1	40,4	72	6.91(-35)	3.18(-26)	2.07(-21)	5.28(-19)	1.46(-17)	1.28(-17)
11,1	41,3	54	1.26(-43)	2.57(-32)	5.29(-26)	7.64(-23)	5.99(-21)	2.07(-21)
11,1	33,1	44	7.33(-44)	3.36(-32)	1.01(-25)	1.74(-22)	1.51(-20)	1.30(-20)
20,2	00,0	313	1.43(-11)	1.50(-11)	1.56(-11)	1.58(-11)	1.60(-11)	1.46(-11)
20,2	11,1	313	2.16(-11)	1.89(-11)	1.73(-11)	1.64(-11)	1.58(-11)	9.95(-12)
20,2	21,1	208	7.44(-15)	1.20(-13)	5.84(-13)	1.32(-12)	2.18(-12)	1.81(-12)
20,2	22,0	141	2.56(-20)	3.49(-17)	1.90(-15)	1.39(-14)	4.55(-14)	4.03(-14)
20,2	31,3	123	3.19(-20)	7.86(-17)	6.01(-15)	5.22(-14)	1.90(-13)	2.41(-13)
20,2	32,2	83	3.67(-29)	1.00(-22)	3.87(-19)	2.42(-17)	2.91(-16)	2.25(-16)
20,2	40,4	72	6.12(-31)	8.34(-24)	7.82(-20)	7.64(-18)	1.20(-16)	7.72(-17)
20,2	41,3	54	1.45(-38)	6.49(-29)	1.51(-23)	7.24(-21)	2.93(-19)	2.52(-19)
20,2	33,1	44	4.04(-40)	5.37(-30)	2.28(-24)	1.49(-21)	7.23(-20)	5.97(-20)
21,1	00,0	208	5.16(-14)	1.06(-13)	1.80(-13)	2.33(-13)	2.67(-13)	1.59(-13)
21,1	11,1	208	4.70(-11)	5.01(-11)	5.30(-11)	5.47(-11)	5.56(-11)	5.20(-11)
21,1	20,2	208	1.04(-11)	1.10(-11)	1.19(-11)	1.27(-11)	1.33(-11)	1.10(-11)
21,1	22,0	141	9.83(-17)	8.69(-15)	1.05(-13)	3.66(-13)	7.75(-13)	7.99(-13)
21,1	31,3	123	6.77(-18)	1.13(-15)	1.97(-14)	8.27(-14)	1.96(-13)	2.20(-13)
21,1	32,2	83	2.70(-25)	4.67(-20)	3.83(-17)	1.09(-15)	8.16(-15)	8.64(-15)
21,1	40,4	72	6.48(-28)	5.72(-22)	1.15(-18)	5.13(-17)	5.00(-16)	4.79(-16)
21,1	41,3	54	1.01(-34)	3.07(-26)	1.61(-21)	3.69(-19)	9.68(-18)	8.84(-18)
21,1	33,1	44	1.04(-36)	9.22(-28)	8.64(-23)	2.65(-20)	8.20(-19)	7.01(-19)
22,0	00,0	141	1.24(-12)	1.35(-12)	1.41(-12)	1.44(-12)	1.47(-12)	1.08(-12)
22,0	11,1	141	1.66(-11)	1.70(-11)	1.70(-11)	1.68(-11)	1.67(-11)	1.82(-11)
22,0	20,2	141	4.64(-12)	5.07(-12)	5.26(-12)	5.29(-12)	5.28(-12)	4.68(-12)
22,0	21,1	141	1.31(-11)	1.39(-11)	1.44(-11)	1.46(-11)	1.48(-11)	1.53(-11)
22,0	31,3	123	6.15(-13)	1.47(-12)	2.31(-12)	2.84(-12)	3.19(-12)	2.97(-12)
22,0	32,2	83	4.20(-20)	9.11(-17)	6.64(-15)	5.69(-14)	2.06(-13)	1.69(-13)
22,0	40,4	72	9.07(-24)	1.10(-19)	2.19(-17)	3.17(-16)	1.60(-15)	1.14(-15)
22,0	41,3	54	1.67(-29)	5.81(-23)	2.49(-19)	1.61(-17)	1.95(-16)	2.03(-16)
22,0	33,1	44	6.15(-30)	6.46(-23)	5.10(-19)	4.50(-17)	6.59(-16)	5.69(-16)

 

 

Table 5: Coefficients $a^{(n)}_{j_2=0;j\alpha \rightarrow j'\alpha '}$ (n = 0 to 4) of the polynomial fit (Eq. (3)) to the rate coefficients of ortho-water in Table 3.

10,1	$a^{(n)}_{\rightarrow 1_{1,0}}$	$a^{(n)}_{\rightarrow 2_{1,2}}$	$a^{(n)}_{\rightarrow 2_{2,1}}$	$a^{(n)}_{\rightarrow 3_{0,3}}$	$a^{(n)}_{\rightarrow 3_{1,2}}$	$a^{(n)}_{\rightarrow 3_{2,1}}$	$a^{(n)}_{\rightarrow 3_{3,0}}$	$a^{(n)}_{\rightarrow 4_{1,4}}$	$a^{(n)}_{\rightarrow 4_{2,3}}$
0	-10.3789	-10.3869	-10.4242	-10.1245	-13.3466	-10.5093	-12.0445	-10.8861	-11.5006
1	-4.7441	-0.2613	-5.6338	-4.8861	11.3629	-9.7223	-5.8542	-1.3445	-7.5809
2	24.9341	0.6404	17.8475	16.4054	-32.8114	29.5880	19.9022	6.4072	23.4461
3	-63.5843	-36.1877	-96.0049	-95.6008	-54.0267	-158.7750	-192.9309	-137.2240	-205.2970
4	33.6533	1.0748	14.5757	14.0471	-17.1286	21.4216	15.8422	7.3395	16.8892
11,0	$a^{(n)}_{\rightarrow 1_{0,1}}$	$a^{(n)}_{\rightarrow 2_{1,2}}$	$a^{(n)}_{\rightarrow 2_{2,1}}$	$a^{(n)}_{\rightarrow 3_{0,3}}$	$a^{(n)}_{\rightarrow 3_{1,2}}$	$a^{(n)}_{\rightarrow 3_{2,1}}$	$a^{(n)}_{\rightarrow 3_{3,0}}$	$a^{(n)}_{\rightarrow 4_{1,4}}$	$a^{(n)}_{\rightarrow 4_{2,3}}$
0	-10.3790	-11.3329	-10.4073	-11.0068	-10.3319	-9.8782	-11.0402	-10.6540	-10.9188
1	-4.7429	6.3667	-1.2021	-1.8128	-4.7552	-18.2030	-9.2674	-10.5835	-4.3408
2	24.9290	-17.4588	6.3569	9.5160	14.9783	53.5639	31.1035	31.8810	13.3318
3	-51.9665	-3.4010	-69.8925	-76.5337	-104.3242	-176.9589	-196.1172	-156.7395	-180.0520
4	33.6462	-8.1578	7.4937	10.7398	12.6088	35.2050	22.9118	21.6240	10.1984
21,2	$a^{(n)}_{\rightarrow 1_{0,1}}$	$a^{(n)}_{\rightarrow 1_{1,0}}$	$a^{(n)}_{\rightarrow 2_{2,1}}$	$a^{(n)}_{\rightarrow 3_{0,3}}$	$a^{(n)}_{\rightarrow 3_{1,2}}$	$a^{(n)}_{\rightarrow 3_{2,1}}$	$a^{(n)}_{\rightarrow 3_{3,0}}$	$a^{(n)}_{\rightarrow 4_{1,4}}$	$a^{(n)}_{\rightarrow 4_{2,3}}$
0	-10.6089	-11.5549	-11.3716	-10.8916	-10.7837	-10.5286	-11.2588	-10.1292	-11.5120
1	-0.2603	6.3682	2.5079	0.9378	1.6764	-3.5781	-8.1435	-8.3748	-4.2104
2	0.6373	-17.4630	-5.9200	2.5525	-2.5947	12.5517	26.4021	25.7030	15.0179
3	-1.3776	19.8017	-29.3305	-45.8541	-60.1146	-102.3052	-166.5589	-126.8035	-160.9790
4	1.0703	-8.1609	-1.0016	7.9531	3.0985	10.9290	19.9855	19.0032	12.6855
22,1	$a^{(n)}_{\rightarrow 1_{0,1}}$	$a^{(n)}_{\rightarrow 1_{1,0}}$	$a^{(n)}_{\rightarrow 2_{1,2}}$	$a^{(n)}_{\rightarrow 3_{0,3}}$	$a^{(n)}_{\rightarrow 3_{1,2}}$	$a^{(n)}_{\rightarrow 3_{2,1}}$	$a^{(n)}_{\rightarrow 3_{3,0}}$	$a^{(n)}_{\rightarrow 4_{1,4}}$	$a^{(n)}_{\rightarrow 4_{2,3}}$
0	-10.6461	-10.6291	-11.3724	-13.0673	-12.0170	-10.0915	-10.0619	-10.3800	-10.2047
1	-5.6341	-1.2025	2.5147	11.2569	6.9286	-3.1601	-4.4991	-10.0755	-10.0538
2	17.8482	6.3577	-5.9381	-25.8984	-8.6326	11.5113	15.6783	29.3176	28.7513
3	-26.5755	-12.0689	5.3138	20.0093	-31.3570	-67.5097	-117.5229	-94.5043	-141.7895
4	14.5678	7.4829	-1.0202	-4.1370	11.9464	11.2662	12.6528	18.8642	19.5192
30,3	$a^{(n)}_{\rightarrow 1_{0,1}}$	$a^{(n)}_{\rightarrow 1_{1,0}}$	$a^{(n)}_{\rightarrow 2_{1,2}}$	$a^{(n)}_{\rightarrow 2_{2,1}}$	$a^{(n)}_{\rightarrow 3_{1,2}}$	$a^{(n)}_{\rightarrow 3_{2,1}}$	$a^{(n)}_{\rightarrow 3_{3,0}}$	$a^{(n)}_{\rightarrow 4_{1,4}}$	$a^{(n)}_{\rightarrow 4_{2,3}}$
0	-10.4976	-11.3806	-11.0451	-13.2231	-10.4944	-11.3084	-11.8466	-10.5371	-10.5972
1	-4.8374	-1.7583	1.0069	11.3465	-3.4844	-3.3325	-2.8068	0.1307	-6.1213
2	16.2259	9.3249	2.3076	-26.2015	12.5320	16.7656	11.6927	3.0931	16.3962
3	-24.7090	-17.2451	-9.6763	21.6127	-43.2403	-78.3356	-111.5536	-63.4955	-123.5756
4	13.8780	10.5731	7.7369	-4.3454	11.8678	19.0277	10.2459	6.1810	10.6898

 

 

Table 6: Coefficients of the polynomial fit (Eq. (3)) to the rate coefficients of para-water in Table 3.

00,0	$a^{(n)}_{\rightarrow 1_{1,1}}$	$a^{(n)}_{\rightarrow 2_{0,2}}$	$a^{(n)}_{\rightarrow 2_{1,1}}$	$a^{(n)}_{\rightarrow 2_{2,0}}$	$a^{(n)}_{\rightarrow 3_{1,3}}$	$a^{(n)}_{\rightarrow 3_{2,2}}$	$a^{(n)}_{\rightarrow 4_{0,4}}$	$a^{(n)}_{\rightarrow 4_{1,3}}$	$a^{(n)}_{\rightarrow 3_{3,1}}$
0	-9.9974	-10.4731	-15.8034	-9.6994	-10.9421	-6.4746	-11.2512	-14.6925	-13.3543
1	-4.1238	2.6873	29.8017	-11.6981	0.6573	-57.8975	-4.5555	10.2500	5.5504
2	16.6079	-6.0654	-72.3553	36.0829	1.3266	172.7658	13.8900	-11.8564	-12.2570
3	-49.8872	-39.5805	0.5622	-134.7151	-94.7562	-360.7653	-157.5076	-188.2216	-167.9145
4	13.9732	-0.1119	-12.5992	24.9535	4.7175	116.9532	9.7020	20.7752	-3.6496
11,1	$a^{(n)}_{\rightarrow 0_{0,0}}$	$a^{(n)}_{\rightarrow 2_{0,2}}$	$a^{(n)}_{\rightarrow 2_{1,1}}$	$a^{(n)}_{\rightarrow 2_{2,0}}$	$a^{(n)}_{\rightarrow 3_{1,3}}$	$a^{(n)}_{\rightarrow 3_{2,2}}$	$a^{(n)}_{\rightarrow 4_{0,4}}$	$a^{(n)}_{\rightarrow 4_{1,3}}$	$a^{(n)}_{\rightarrow 3_{3,1}}$
0	-10.4760	-11.3828	-10.5967	-10.1736	-10.3632	-11.4142	-11.2061	-13.4431	-11.9383
1	-4.1109	5.1435	4.5018	-4.2417	-3.5859	-0.4472	0.7173	4.7008	-1.5315
2	16.5666	-12.8492	-11.8574	15.9061	11.2659	5.0774	-0.5198	-6.3091	6.5207
3	-26.6238	-5.2013	-24.7220	-86.3470	-83.1425	-118.5232	-117.2276	-157.9642	-166.4029
4	13.9434	-6.4753	-3.4580	13.2265	10.0649	9.2072	2.1318	13.1971	6.4090
20,2	$a^{(n)}_{\rightarrow 0_{0,0}}$	$a^{(n)}_{\rightarrow 1_{1,1}}$	$a^{(n)}_{\rightarrow 2_{1,1}}$	$a^{(n)}_{\rightarrow 2_{2,0}}$	$a^{(n)}_{\rightarrow 3_{1,3}}$	$a^{(n)}_{\rightarrow 3_{2,2}}$	$a^{(n)}_{\rightarrow 4_{0,4}}$	$a^{(n)}_{\rightarrow 4_{1,3}}$	$a^{(n)}_{\rightarrow 3_{3,1}}$
0	-11.1739	-11.6110	-10.9854	-10.9788	-10.5715	-10.7710	-10.4586	-12.7111	-13.1334
1	2.7033	5.2053	3.0807	-3.7934	-0.2219	-3.9628	-5.3168	4.5269	5.8649
2	-6.1182	-13.0745	-13.6358	15.7831	4.0774	13.6220	15.7231	-11.8668	-16.8304
3	4.2901	15.7584	4.5238	-67.6138	-54.9645	-108.2711	-117.2091	-115.8773	-114.2936
4	-0.1446	-6.6583	-10.1398	14.7956	6.8654	14.0995	12.1368	-4.6166	-9.1990
21,1	$a^{(n)}_{\rightarrow 0_{0,0}}$	$a^{(n)}_{\rightarrow 1_{1,1}}$	$a^{(n)}_{\rightarrow 2_{0,2}}$	$a^{(n)}_{\rightarrow 2_{2,0}}$	$a^{(n)}_{\rightarrow 3_{1,3}}$	$a^{(n)}_{\rightarrow 3_{2,2}}$	$a^{(n)}_{\rightarrow 4_{0,4}}$	$a^{(n)}_{\rightarrow 4_{1,3}}$	$a^{(n)}_{\rightarrow 3_{3,1}}$
0	-16.4968	-10.8369	-10.9983	-9.8342	-10.3130	-10.7596	-11.3061	-11.0861	-12.0892
1	29.7469	4.6805	3.2181	-8.6413	-7.1411	0.5537	-0.7842	-2.1446	-0.5204
2	-72.1527	-12.5063	-14.1846	28.4892	21.2772	1.2362	3.9445	6.9918	2.5470
3	59.6970	12.5799	21.1504	-67.4964	-58.5062	-76.1090	-86.4823	-124.3064	-124.2489
4	-12.3982	-3.9974	-10.6578	22.5416	14.9127	5.7028	4.4782	6.9657	3.3339
22,0	$a^{(n)}_{\rightarrow 0_{0,0}}$	$a^{(n)}_{\rightarrow 1_{1,1}}$	$a^{(n)}_{\rightarrow 2_{0,2}}$	$a^{(n)}_{\rightarrow 2_{1,1}}$	$a^{(n)}_{\rightarrow 3_{1,3}}$	$a^{(n)}_{\rightarrow 3_{2,2}}$	$a^{(n)}_{\rightarrow 4_{0,4}}$	$a^{(n)}_{\rightarrow 4_{1,3}}$	$a^{(n)}_{\rightarrow 3_{3,1}}$
0	-10.3972	-10.3940	-10.9777	-9.8348	-10.4334	-10.5110	-12.6026	-11.8090	-10.6685
1	-11.7096	-4.2531	-3.8024	-8.6350	-9.1989	-0.0096	7.1506	2.2873	0.4973
2	36.1275	15.9426	15.8180	28.4687	34.6227	2.3748	-27.5952	-2.6543	0.8718
3	-49.6940	-24.5160	-26.3855	-41.8535	-58.1543	-52.4147	-14.3669	-88.8274	-97.3576
4	24.9949	13.2622	14.8394	22.5386	29.0011	6.9352	-19.7570	3.1452	2.9082