2 Calculational method and convergence of the collisional cross sections

Close coupling and coupled states calculations are done with the MOLSCAT (Hutson & Green 1994) code and with Green's code of the PES of Phillips et al. (1994). The water molecule is described by a version of the effective Hamiltonian of Kyrö (1981), compatible with the symmetries of the PES. We use the molecular constants of Table 1 of Kyrö (1981) and our calculated rotational levels of H₂¹⁶O are identical to those of Green et al. (1993). The reduced mass of the system is 1.81277373 a.m.u. and the hydrogen molecule is taken as a rigid rotor with a rotational constant of 60.853 cm^-1 .

 

 

Table 1: Propagation parameters of MOLSCAT and basis set used in our calculations (see the MOLSCAT documentation (Hutson & Green 1994) for the meaning of the parameters). (1) and (2) refer to the parameters used respectively for ortho and para water.

Propagation parameters
INTFLG = 6	STEPS = 10
DTOL = 0.3	OTOL = 0.005
(1)RMIN = 1.2 (adjusted)	(1)IRMSET = 10	(1)RMAX = 40. (adjusted)
(2)RMIN = 1. (adjusted)	(2)IRMSET = 0	(2)RMAX = 50. (adjusted)
Basis set B(j, j2)
1 closed j-channel for H20
1 or 0 closed j2-channel for H2	(as indicated in the text)

Our first step was to assess the correctness of our results with respect to those of Phillips et al. (1995). We re-calculated the inelastic cross sections for all symetries and at the energies given in Tables 1 and 2 of Phillips et al. (1995). Most of our inelastic cross sections, calculated with the parameters values given in Table 1, are in excellent agreement with those of Phillips et al. (1995). Table 2 shows the few CC cross sections that do not agree very well.

 

 

Table 2: Cross-sections that are in disagreement with data given in Tables 1 and 2 of Phillips et al. (1995). All data are obtained using the diabatic modified log-derivative propagator of Manolopoulos (1986) and the basis set B(5, 2). The collision energy is given in cm^-1 and cross sections are in Ų. The levels are labelled with j_K-1K1.

Energy	Initial	Final	Our values	Phillips's	Relative difference
para-H2O/para-H2
47	00,0	11,1	2.85	2.91	2%
300	32,2	33,1	0.73	0.71	2.8%
ortho-H2O/para-H2
123.79	10,1	21,2	1.99	1.94	2.6%
300	31,2	32,1	1.13	1.10	2.7%
	32,1	33,0	0.80	0.77	3.9%
	33,0	41,4	0.52	0.49	6.1%

We tested the convergence of the results with respect to the parameters in Table 1, for the two propagators used by Phillips et al. (1995, 1996), namely the diabatic modified log-derivative method of Manolopoulos (1986) (parameter $\rm INTFLG=6$ in MOLSCAT) and the hydrid propagator of Alexander & Manolopoulos (1987) (parameter $\rm INTFLG=8$ in MOLSCAT). We tested these propagators both with and without an automatic search for the starting point, meaning that the parameter IRMSET is either varied until convergence is obtained or set to zero. This gives 4 different methods for each of CC and CS calculations. For both propagators the parameters to be optimized are the number of steps per half wave number at the lowest energy (STEPS), the maximum range of propagation (RMAX) and either the starting point of propagation (RMIN) if it is set fixed or the initial wavefunction amplitude in all channels (less than 10**(-IRMSET)). For the hybrid propagator additional parameters (RMID or RVFAC, DRAIRY), managing the transition between the short and the long range propagations, must be optimized. We performed the convergence tests of the CC and CS cross sections of the transition $0_{0,0}\rightarrow 1_{1,1}$ at 47 cm^-1 with the basis set B(5, 0). All methods converge at better than 0.5% towards a value of 1.435 Å²in CS and 2.265 Å² in CC; these values are in slight disagreement with the Phillips et al. (1995) values of 1.48 Å² in CS and 2.41 Å² in CC. It is difficult to be certain about the origin of this disagreement, however the convergence of all our tests to the same values gives us confidence in our results. It should be noted, when using the hybrid propagator, that a non negative value of the RVFAC parameter coupled with an automatic search for the starting point of the short range propagation, allows an automatic search for the starting point for the long range propagation. This association of methods is unstable and requires an optimisation of the parameter RVFAC at different energies and for each angular coupling case.

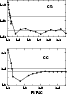Figure 1: The convergence of the CC and CS cross sections (in Å2) of the $0_{0,0}\rightarrow 1_{1,1}$ transition with respect to the parameter RVFAC ( $\rm INTFLG=8$) is shown together with the Phillips et al. (1995) values (dotted lines) and our converged values (dashed lines) obtained with $\rm INTFLG=6$. The basis set is B(5, 0) and the total energy is 47 cm-1. The other parameters are given in Table 1.

Figure 1 shows the convergence of the $0_{0,0}\rightarrow 1_{1,1}$ cross section with respect to the parameter RVFAC. We note that different optimized values of RVFAC are obtained in CC and CS calculations, showing that the CC and CS calculations converge for different values of RVFAC. Although we were able to obtain convergence, we do not recommend the use of this association of methods, i.e. the use of $\rm INTLFLG=8$, IRMSET non-zero and RVFAC positive, with the presently available version of the MOLSCAT code (Hutson & Green 1994). In the following calculations we choose the diabatic modified log-derivative method of Manolopoulos (1986) with or without an automatic search for the short range propagation, which provides about 1% accuracy in the cross sections and stability of the parameters from one angular coupling case to the next.