Alkali earth atoms in a 1P state have an electronic angular momentum L=1 and an electronic spin S=0, so the angular momentum of the radiating atom is J=1. Combining J with the angular momentum j2=1/2 of the H atom, we obtain the total angular momentum j=1/2,3/2. The relevant channels for a total angular momentum ![]() are given in Appendix A. So, for each kinetic energy, two sets of three-channel scattering equations were solved for a given value of the total angular momentum
are given in Appendix A. So, for each kinetic energy, two sets of three-channel scattering equations were solved for a given value of the total angular momentum ![]() ranging from 1.5 to some suitable large value (up to 700.5 at the highest energies) in order to obtain convergence of the summation.
ranging from 1.5 to some suitable large value (up to 700.5 at the highest energies) in order to obtain convergence of the summation.
As inelastic cross sections to other states are negligible, we have only to consider the collisional relaxation rates of rank 0, 1 and 2. The corresponding cross sections are given by:
| (9) |
We give here the explicit expressions of the
![]() in terms of the Grawert coefficients B were given by Reid (1973) for J=1/2 and J=3/2.
in terms of the Grawert coefficients B were given by Reid (1973) for J=1/2 and J=3/2.
Explicit expressions of the tensorial tranfer cross sections between J=1/2 and J=3/2 states are the following:
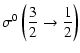 |
= | ![$\displaystyle \frac{1}{2\sqrt{2}}\left[3B\left(\frac{1}{2}\frac{3}{2};1\right)+5B\left(\frac{1}{2}\frac{3}{2};2\right)\right]$](/articles/aa/full/2002/29/aa2344/img96.gif) |
|
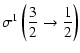 |
= | ![$\displaystyle \sigma^1\left(\frac{1}{2}\rightarrow\frac{3}{2}\right)=\frac{\sqr...
...t(\frac{1}{2}\frac{3}{2};1\right)-B\left(\frac{1}{2}\frac{3}{2};2\right)\right]$](/articles/aa/full/2002/29/aa2344/img98.gif) |
|
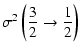 |
= | 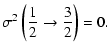 |
(10) |
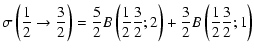 |
(11) |
The calculated relaxation rates, polarization transfer rates and fine structure transfer rate are presented in Figs. 7, 8 and 9. All these rates increase slowly with the temperature. As mentioned previously, the relaxation rates are larger than the transfer rates, the polarization transfer rate
g1(1/2,3/2) being almost negligible in comparison with the
![]() and
and
![]() coefficients. We remark that the differences between g1(1/2) and g3(3/2) are nowhere discernible to the resolution of the figure, this results from compensation of the two components of the relaxation cross sections (see Eq. (6)). The same trend was obtained by Wilson & Shimoni (1975) for Na(3p 2P
coefficients. We remark that the differences between g1(1/2) and g3(3/2) are nowhere discernible to the resolution of the figure, this results from compensation of the two components of the relaxation cross sections (see Eq. (6)). The same trend was obtained by Wilson & Shimoni (1975) for Na(3p 2P
![]() collisions. Table 2 shows a comparison of our calculated fine structure rate with previous results. We note a significant difference in these values due to the different potential energy curves used, nevertheless our values are very similar to those obtained by Monteiro et al. 1985 from potential energy curves that include correctly the ionic configuration in the
collisions. Table 2 shows a comparison of our calculated fine structure rate with previous results. We note a significant difference in these values due to the different potential energy curves used, nevertheless our values are very similar to those obtained by Monteiro et al. 1985 from potential energy curves that include correctly the ionic configuration in the
![]() molecular states. This indicates the importance of an accurate description of the potential energy curves in the intermediate and large internuclear distances.
molecular states. This indicates the importance of an accurate description of the potential energy curves in the intermediate and large internuclear distances.
| T(K) | 4000 | 4500 | 5000 | 6000 | 7000 | 8000 | 9000 | 10 000 |
| This work | 7.45 | 8.87 | 8.26 | 8.93 | 9.49 | 9.95 | 10.33 | 10.65 |
| (Monteiro et al. 1985) | - | - | 8.06 | 8.62 | 9.16 | 9.7 | 10.04 | - |
| (Roueff 1974) | - | 5.12 | - | 5.61 | 5.95 | - | 6.45 | 6.75 |
| (Lewis et al. 1971) | - | - | 3.03 | - | - | - | - | - |
The generalization of Eq. (2) with J=J' to include the effects of nuclear spin has
been studied by (Omont 1977). We consider the case of a single hyperfine
multiplet, with electronic angular momentum J and with nuclear spin I. The total angular momentum F takes the values
![]() and we may consider possible off diagonal
elements of the corresponding density matrix. The density matrix
and we may consider possible off diagonal
elements of the corresponding density matrix. The density matrix
![]() can be expanded as (Omont 1977):
can be expanded as (Omont 1977):
 |
(12) |
| TKQ(FF') | = | ||
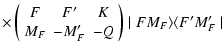 |
(13) |
The unitary transformation from the
basis
TKQ(FF') to the basis
![]() is given by:
is given by:
| TKQ(FF') | = | ||
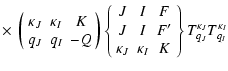 |
(14) |
| = | |||
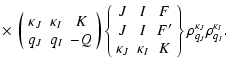 |
(15) |
![$\displaystyle {\frac{{\rm d} [\hfill^{(\lambda J)}\rho^{K}_{Q}(FF')]}{{\rm d}t} =-\sum _{
F''F'''}G_{K}(FF',F''F''')[\hfill^{(\lambda J)}\rho
^{K}_{Q}(F''F''')]}$](/articles/aa/full/2002/29/aa2344/img128.gif) | |||
| (16) | |||
| GK(FF', F''F''') = [(2F+1)(2F'+1)]1/2 | |||
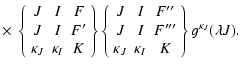 |
(17) | ||
| QK(FF',F''F''')=[ (2F+1)(2F'+1)]1/2 | |||
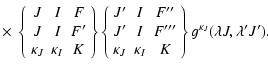 |
(18) | ||
As previously mentioned in the case of the multipole relaxation of the hyperfine levels in the ground state the algebra coefficients are a fraction of one and thus all the collisional rates among the excited hyperfine levels are of the same order of magnitude as the
![]() coefficients of the fine structure 2P1/2 and 2P3/2 levels.
coefficients of the fine structure 2P1/2 and 2P3/2 levels.
Cross sections were averaged over a Maxwell distribution of
velocities. The variation of the relaxation rates with
the temperature is very smooth and was found to increase as ![]() and is given as follows for 200 K
and is given as follows for 200 K ![]()
![]() K.
K.
Mg(1P![]() :
:
g1=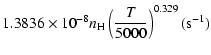 |
|
g2=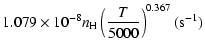 |
(19) |
Ca(1P)+H:
g1=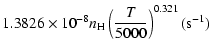 |
|
g2=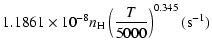 |
(20) |
g1=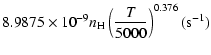 |
|
g2=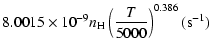 |
(21) |
| J=1/2 | 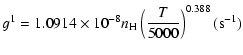 |
(22) | |
| J=3/2 | 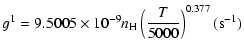 |
||
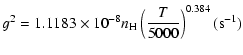 |
|||
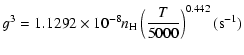 |
(23) |
| = | |||
| = | 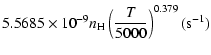 |
||
| = | |||
| = | 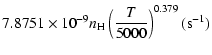 |
||
| = | |||
| = | 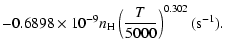 |
(24) |
Copyright ESO 2002